The Brewster angle of incidence could be obtained for both the TE and TM polarizations.
In the case of the TE‐polarization , at an incident angle θ 1= θ B, i.e. at Brewster angle the reflection coefficient 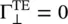 . So from equation (5.2.8c), and also using the Snell's refraction law (5.2.7b), the following expression for Brewster angle is obtained:
. So from equation (5.2.8c), and also using the Snell's refraction law (5.2.7b), the following expression for Brewster angle is obtained:
(5.3.1) 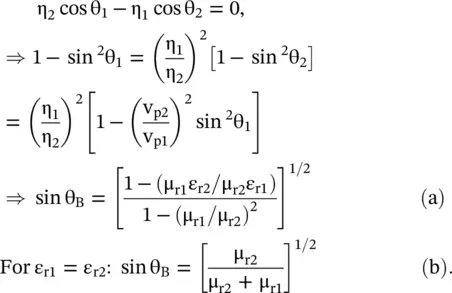
The above relation applies to a magnetodielectric medium . However, if both media are dielectrics i.e. μ r1= μ r2= 1 then sin θ B→ ∞. Thus, the Brewster angle does not exist at the interface of two dielectric media . The Brewster angle could exit for the case (b). Such a material is difficult to get in practice. However, the situation is different for the TM‐polarized plane wave.
In the case of the TM‐polarization , again the reflection is zero, i.e. 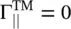 , at θ 1= θ B. Using equation (5.2.16c), and the Snell's refraction law; the Brewster angle is obtained:
, at θ 1= θ B. Using equation (5.2.16c), and the Snell's refraction law; the Brewster angle is obtained:
(5.3.2) 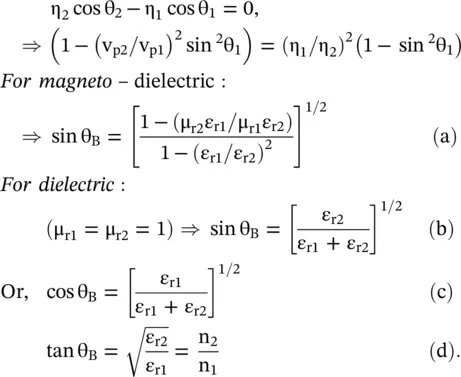
Unlike the TE polarization, the Brewster angle of the TM‐polarized obliquely incident wave exists even at the interface of the nonmagnetic dielectric medium. Thus, the Brewster angle could be used to separate the TE and TM polarizations from the obliquely incident unpolarized wave at the interface of two dielectric media, as only the TE‐polarized wave component will get reflected. A Brewster angle is also called the polarizing angle .
At the critical angle of incidence (θ 1= θ c), complete reflection occurs at the interface. It occurs for both the TE and TM polarizations. The transmission line model helps to understand it. In the case of a terminated line, total reflection occurs for the load impedance Z L= 0, ∞ , ± jX. In the first case, the line is short‐circuited, i.e. terminated in a PEC with ε r→ ∞, in the second case, the line is open‐circuited, i.e. terminated in a PMC with μ r→ ∞; in the third case, the line is terminated in a RIS, either inductive or capacitive. The corresponding surface, i.e. the interface, is a PEC, or PMC, or RIS. These surfaces are further discussed in chapter 20for the artificially engineered periodic surfaces known as the electromagnetic bandgap (EBG) surfaces. By varying the angle of incidence of both polarizations with respect to the critical angle of incidence, the reflection and transmission of waves could be controlled.
Figure (5.3)shows that in the case TM – polarized wave, total reflection at the critical angle, is obtained by taking the load impedance at the interface (x = 0 +) zero. Likewise, for the TE – polarization shown in Fig (5.2), total reflection at a critical angle is obtained for the infinite load impedance at the interface. Using equations, the following conditions are obtained: for TM‐polarization, Z L= η 2cos θ 2= 0; for TE polarization, Z L= − η 2/ cos θ 2= ∞. Both cases give the following expression for the critical angle θ 1= θ cand Snell's Law of refraction:
(5.3.3) 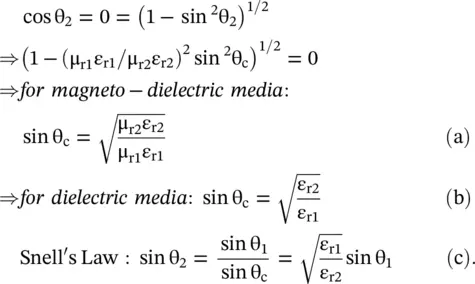
For the real value of the critical angle θ c, permittivities of media are taken as ε r1> ε r2. Thus, the critical angle of the interface is a fixed quantity. The angle of refraction θ 2deciding the direction of wave propagation in medium #2 is a function of angle incidence θ 1. Figure (5.5a–c), applicable to for both the TM and TE polarizations, consider three cases, θ 1< θ c, θ 1= θ c, θ 1> θ c, of propagation for the obliquely incident plane wave.
In this case, equation (5.3.3c)provides the real value of the angle θ 2as sinθ 2< 1 corresponding to an angle of incidence θ 1. Figure (5.5a)shows the reflection and transmission of the obliquely incident plane wave at the interface for the case ε r1> ε r2.
Figure (5.5b)shows the case for θ 1= θ c. The angle of refraction θ 2is obtained on substituting sinθ 1= sin θ cin equation (5.3.3c):
(5.3.4) 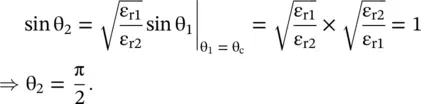
Figure (5.5b)shows that the refracted wave travels along the interface x = 0 +in the y‐direction and no component of the refracted (transmitted) wave propagates in the medium #2. Equation (5.2.28a)also shows that for the TM‐polarized incident wave, the reflection coefficient is 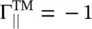 at the angle of refraction θ 2= π/2. It demonstrates that under the total reflection condition, occurring at the critical angle θ 1= θ c, the interface behaves as a PEC for the TM‐polarized incident wave. However, equation (5.2.28b)provides also a transmission coefficient
at the angle of refraction θ 2= π/2. It demonstrates that under the total reflection condition, occurring at the critical angle θ 1= θ c, the interface behaves as a PEC for the TM‐polarized incident wave. However, equation (5.2.28b)provides also a transmission coefficient 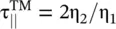 . It shows that the transmitted wave in the medium #2, confined at the interface, travels along the y‐axis at the interface x = 0 +. The transmitted field components at an angle θ 2= π/2 in the medium #2 are given in equation (5.2.18).
. It shows that the transmitted wave in the medium #2, confined at the interface, travels along the y‐axis at the interface x = 0 +. The transmitted field components at an angle θ 2= π/2 in the medium #2 are given in equation (5.2.18).
In the case of the TE polarization of the obliquely incident wave, equation (5.2.27a,b)shows the reflection coefficient 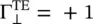 and transmission coefficient
and transmission coefficient 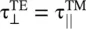 . In this case, the interface acts like a PMC . Again, the transmitted wave in the medium #2 propagates in the y‐direction at the interface x = 0 +. It is seen from the field equation (5.2.10)for θ 2= π/2.
. In this case, the interface acts like a PMC . Again, the transmitted wave in the medium #2 propagates in the y‐direction at the interface x = 0 +. It is seen from the field equation (5.2.10)for θ 2= π/2.
Figure (5.5c)shows the case for θ 1> θ c. Equation (5.3.3c)of Snell's refraction law shows that sinθ 2> 1. Therefore, there is no real solution to the angle θ 2. However, the wave propagation in medium #2 requires sinθ 2and cosθ 2, not the value of the angle of refraction θ 2. The sinθ 2and cosθ 2could be obtained from Snell's Law given by equation (5.2.7c), also from the wavevector k 2and its x and y‐directed components k 2xand k 2yusing equation (5.2.1):
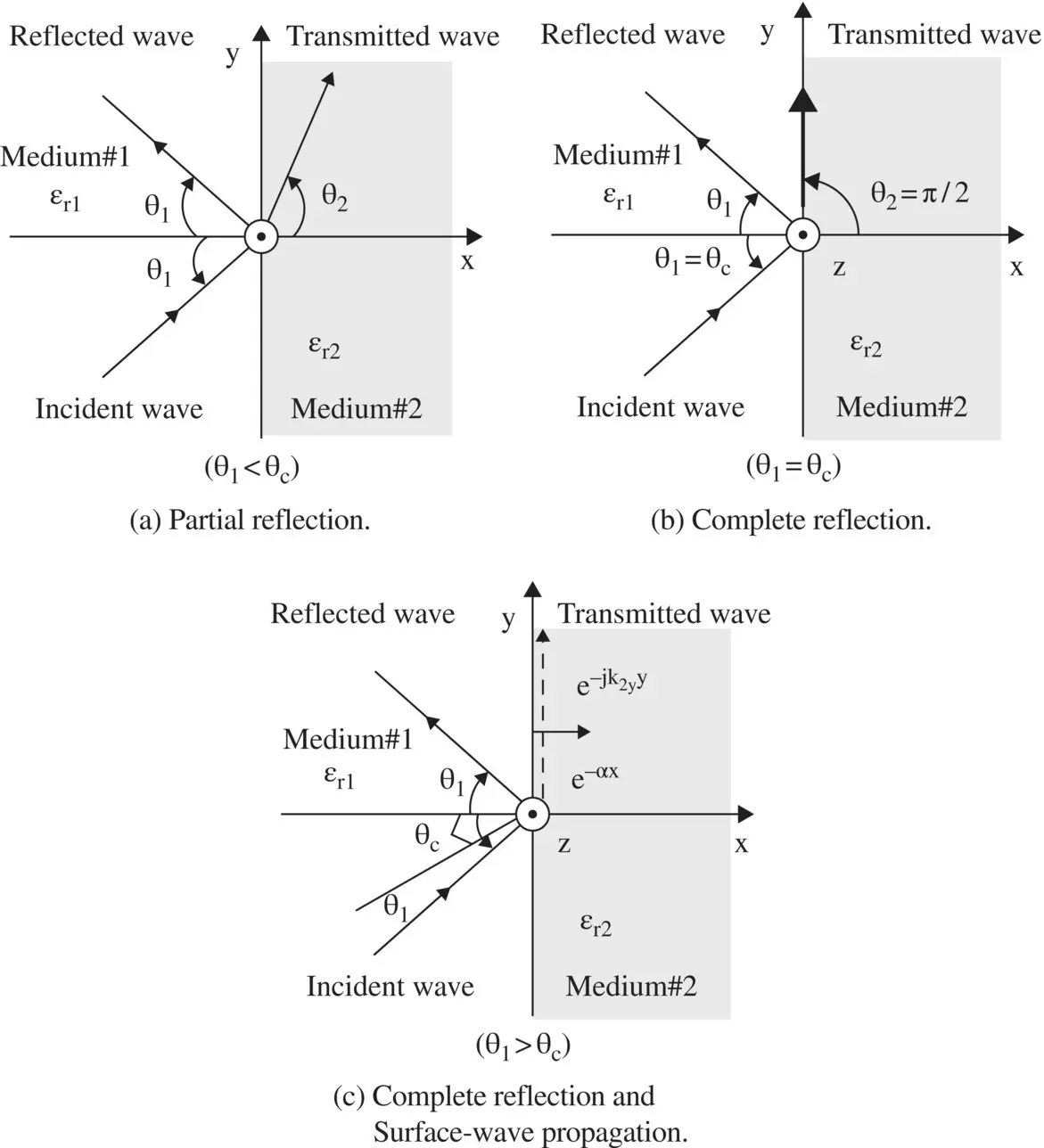
Figure 5.5 Oblique incidence of plane wave at three different angles of incidence.
Читать дальше

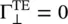 . So from equation (5.2.8c), and also using the Snell's refraction law (5.2.7b), the following expression for Brewster angle is obtained:
. So from equation (5.2.8c), and also using the Snell's refraction law (5.2.7b), the following expression for Brewster angle is obtained: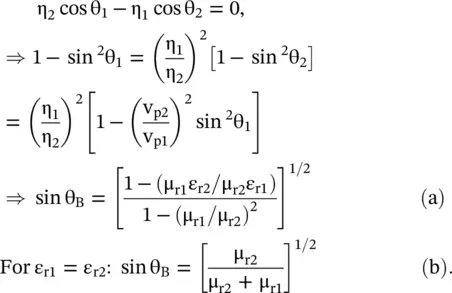
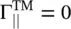 , at θ 1= θ B. Using equation (5.2.16c), and the Snell's refraction law; the Brewster angle is obtained:
, at θ 1= θ B. Using equation (5.2.16c), and the Snell's refraction law; the Brewster angle is obtained: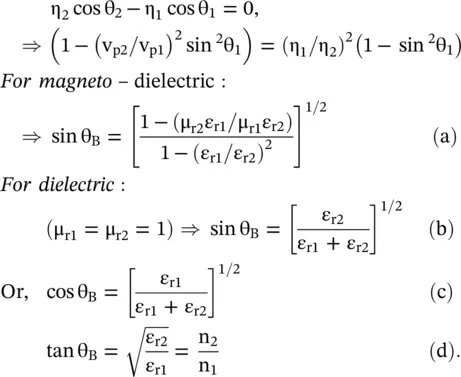
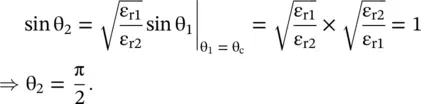
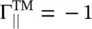 at the angle of refraction θ 2= π/2. It demonstrates that under the total reflection condition, occurring at the critical angle θ 1= θ c, the interface behaves as a PEC for the TM‐polarized incident wave. However, equation (5.2.28b)provides also a transmission coefficient
at the angle of refraction θ 2= π/2. It demonstrates that under the total reflection condition, occurring at the critical angle θ 1= θ c, the interface behaves as a PEC for the TM‐polarized incident wave. However, equation (5.2.28b)provides also a transmission coefficient 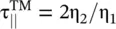 . It shows that the transmitted wave in the medium #2, confined at the interface, travels along the y‐axis at the interface x = 0 +. The transmitted field components at an angle θ 2= π/2 in the medium #2 are given in equation (5.2.18).
. It shows that the transmitted wave in the medium #2, confined at the interface, travels along the y‐axis at the interface x = 0 +. The transmitted field components at an angle θ 2= π/2 in the medium #2 are given in equation (5.2.18).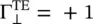 and transmission coefficient
and transmission coefficient 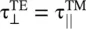 . In this case, the interface acts like a PMC . Again, the transmitted wave in the medium #2 propagates in the y‐direction at the interface x = 0 +. It is seen from the field equation (5.2.10)for θ 2= π/2.
. In this case, the interface acts like a PMC . Again, the transmitted wave in the medium #2 propagates in the y‐direction at the interface x = 0 +. It is seen from the field equation (5.2.10)for θ 2= π/2.











