It is obvious that while the input signal has only one frequency ω, shown in Fig. (4.2), the output of a nonlinear medium has several harmonically related frequency components, ω, 2ω, 3ω, … and so forth. Thus, a sinusoidal input signal gets distorted, once it passes through a nonlinear medium. Such distortion also occurs in an amplifier in the nonlinear region.
Similarly, the relative permeability of a nonlinear magnetic medium is a function of the amplitude of the magnetic field. The constitutive relation, given by equation (4.1.7b), is written as
(4.2.3) 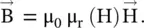

Figure 4.2 Response of nonlinear medium showing generation of harmonics.
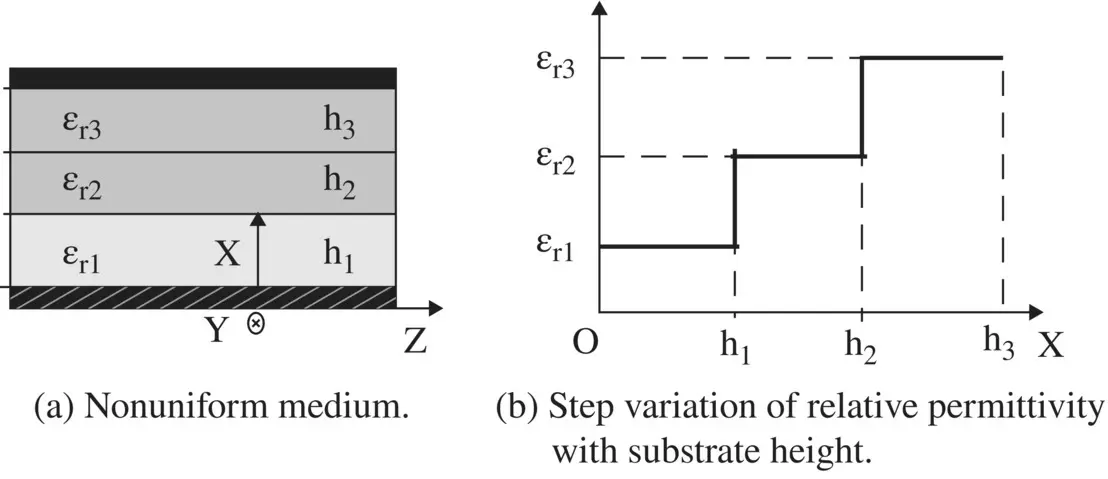
Figure 4.3 Inhomogeneous medium showing a step variation of relative permittivity with substrate height.
where μ r(H) = μ r1+ μ r2H + μ r3H 2+ ⋯ and so forth. The coefficients μ r2, μ r3, … indicate the order of nonlinearity in the nonlinear relative permeability of a magnetic medium.
4.2.2 Homogeneous and Nonhomogeneous Medium
The relative permittivity (ε r) and the permeability (μ r) are not necessarily uniform throughout the volume of a medium. These parameters could also be position‐dependent. The variation in ε rand μ rcould be in discrete steps, or they could be continuous functions of the position. Likewise, the conductivity of a medium can also be a function of position. If the parameters ε r, μ r, and σ are uniform throughout the medium, the medium is called homogeneous ; otherwise, it is a nonhomogeneous medium or an inhomogeneous medium. A multilayer dielectric medium, forming a parallel capacitor, as shown in Fig. (4.3), is a nonhomogeneous medium, where the relative permittivity ε r(x) is a function of position x in discrete steps. The conductivity of a doped Si substrate is a function of the depth of penetration of the charged carrier, forming a continuously variable nonhomogeneous medium.
4.2.3 Isotropic and Anisotropic Medium
Inside the isotropic dielectric medium , the electric displacement vector 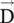 and the electric field intensity
and the electric field intensity 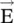 are parallel to each other, i.e. the applied electric field views the same relative permittivity of a medium in all directions. Likewise, the magnetic displacement vector
are parallel to each other, i.e. the applied electric field views the same relative permittivity of a medium in all directions. Likewise, the magnetic displacement vector 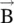 is parallel to the magnetic field intensity
is parallel to the magnetic field intensity 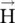 within the isotropic medium. These properties are expressed through constitutive relations (4.1.7a)and (4.1.7b). For the isotropic media, permittivity and permeability are scalar quantities.
within the isotropic medium. These properties are expressed through constitutive relations (4.1.7a)and (4.1.7b). For the isotropic media, permittivity and permeability are scalar quantities.
However, there are dielectrics, such as quartz, sapphire, alumina, MgO, and so forth, where 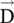 and
and 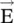 are not parallel to each other, i.e. they are not in the same direction. Such dielectrics form the anisotropic medium. In such a medium, the relative permittivity viewed by the applied electric field is direction‐dependent. For instance, Fig. (4.3a)forms a composite anisotropic medium as the effective permittivity along the x‐axis is different from the effective permittivity along the z‐axis. Similarly, magnetic materials such as ferrite, garnet, and so forth are also anisotropic because
are not parallel to each other, i.e. they are not in the same direction. Such dielectrics form the anisotropic medium. In such a medium, the relative permittivity viewed by the applied electric field is direction‐dependent. For instance, Fig. (4.3a)forms a composite anisotropic medium as the effective permittivity along the x‐axis is different from the effective permittivity along the z‐axis. Similarly, magnetic materials such as ferrite, garnet, and so forth are also anisotropic because 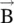 and
and 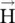 vectors are not in the same direction. Several authors have treated the properties of anisotropic medium and EM‐wave propagation through such media in detail [B.1–B.4, B.9, B.11, B.13–B.15, B.17–B.23]. This subsection reviews basic concepts related to anisotropic media.
vectors are not in the same direction. Several authors have treated the properties of anisotropic medium and EM‐wave propagation through such media in detail [B.1–B.4, B.9, B.11, B.13–B.15, B.17–B.23]. This subsection reviews basic concepts related to anisotropic media.
The relative permittivity and relative permeability of these anisotropic media are not scalar quantities. They are tensor quantity, 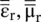 described by 3 × 3 matrices. The constitutive relations of such electric and magnetic media are written as follows:
described by 3 × 3 matrices. The constitutive relations of such electric and magnetic media are written as follows:
(4.2.4) 
In general, elements of permittivity and permeability matrices could be complex quantities and also frequency‐dependent, accounting for the losses and dispersion in the material medium. Equation (4.2.4a)shows that for the anisotropic dielectric medium, the electric flux density 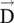 is not parallel to electric field intensity
is not parallel to electric field intensity 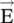 . Likewise, equation (4.2.4b)shows that the vector
. Likewise, equation (4.2.4b)shows that the vector 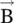 is not parallel to the vector
is not parallel to the vector 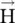 . For instance, if the incident field on an anisotropic dielectric medium has only E xcomponent, i.e. x‐polarized incident E‐field, it generates all three components of electric flux density – D x, D y, and D z. The same applies to the anisotropic magnetic medium.
. For instance, if the incident field on an anisotropic dielectric medium has only E xcomponent, i.e. x‐polarized incident E‐field, it generates all three components of electric flux density – D x, D y, and D z. The same applies to the anisotropic magnetic medium.
The above equations can be written in a more compact form as
(4.2.5) 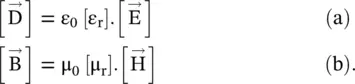
The above permittivity and permeability matrices could be either symmetric or anti‐symmetric. Thus, the anisotropic materials could be divided into two broad groups: (i) symmetric anisotropic materials and (ii) anti‐symmetric anisotropic materials . The symmetric anisotropic materials support linearly polarized EM‐waves propagating as the normal modes of the homogeneous unbounded medium. However, circularly polarized EM‐waves are the normal modes of the anti‐symmetric anisotropic medium. The normal modes of media travel without any change in polarization.
Symmetric Anisotropic Materials
Читать дальше

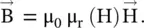


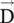 and the electric field intensity
and the electric field intensity 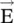 are parallel to each other, i.e. the applied electric field views the same relative permittivity of a medium in all directions. Likewise, the magnetic displacement vector
are parallel to each other, i.e. the applied electric field views the same relative permittivity of a medium in all directions. Likewise, the magnetic displacement vector 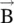 is parallel to the magnetic field intensity
is parallel to the magnetic field intensity 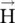 within the isotropic medium. These properties are expressed through constitutive relations (4.1.7a)and (4.1.7b). For the isotropic media, permittivity and permeability are scalar quantities.
within the isotropic medium. These properties are expressed through constitutive relations (4.1.7a)and (4.1.7b). For the isotropic media, permittivity and permeability are scalar quantities.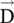 and
and 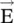 are not parallel to each other, i.e. they are not in the same direction. Such dielectrics form the anisotropic medium. In such a medium, the relative permittivity viewed by the applied electric field is direction‐dependent. For instance, Fig. (4.3a)forms a composite anisotropic medium as the effective permittivity along the x‐axis is different from the effective permittivity along the z‐axis. Similarly, magnetic materials such as ferrite, garnet, and so forth are also anisotropic because
are not parallel to each other, i.e. they are not in the same direction. Such dielectrics form the anisotropic medium. In such a medium, the relative permittivity viewed by the applied electric field is direction‐dependent. For instance, Fig. (4.3a)forms a composite anisotropic medium as the effective permittivity along the x‐axis is different from the effective permittivity along the z‐axis. Similarly, magnetic materials such as ferrite, garnet, and so forth are also anisotropic because 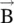 and
and 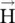 vectors are not in the same direction. Several authors have treated the properties of anisotropic medium and EM‐wave propagation through such media in detail [B.1–B.4, B.9, B.11, B.13–B.15, B.17–B.23]. This subsection reviews basic concepts related to anisotropic media.
vectors are not in the same direction. Several authors have treated the properties of anisotropic medium and EM‐wave propagation through such media in detail [B.1–B.4, B.9, B.11, B.13–B.15, B.17–B.23]. This subsection reviews basic concepts related to anisotropic media.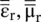 described by 3 × 3 matrices. The constitutive relations of such electric and magnetic media are written as follows:
described by 3 × 3 matrices. The constitutive relations of such electric and magnetic media are written as follows:
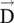 is not parallel to electric field intensity
is not parallel to electric field intensity 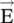 . Likewise, equation (4.2.4b)shows that the vector
. Likewise, equation (4.2.4b)shows that the vector 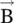 is not parallel to the vector
is not parallel to the vector 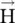 . For instance, if the incident field on an anisotropic dielectric medium has only E xcomponent, i.e. x‐polarized incident E‐field, it generates all three components of electric flux density – D x, D y, and D z. The same applies to the anisotropic magnetic medium.
. For instance, if the incident field on an anisotropic dielectric medium has only E xcomponent, i.e. x‐polarized incident E‐field, it generates all three components of electric flux density – D x, D y, and D z. The same applies to the anisotropic magnetic medium.











