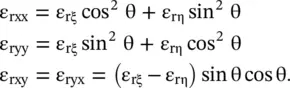The complex permittivity matrix 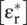 , showing the permittivity tensor, of symmetric anisotropic dielectric material is a Hermitian symmetric matrix, i.e. the following relation holds:
, showing the permittivity tensor, of symmetric anisotropic dielectric material is a Hermitian symmetric matrix, i.e. the following relation holds:
(4.2.6) 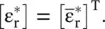
In the above equation, the matrix elements 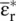 are the complex conjugate of the matrix elements
are the complex conjugate of the matrix elements 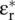 . The superscript T shows the transpose of the permittivity matrix. The above relation also holds for a real permittivity tensor of symmetric anisotropic dielectric material. In a dielectric material case, the off‐diagonal elements of the matrix are symmetrical, i.e. ε r, xy= ε r, yx, and so forth. Similar expression can also be obtained for the symmetric anisotropic magnetic material. However, some media do not follow this symmetry rule.
. The superscript T shows the transpose of the permittivity matrix. The above relation also holds for a real permittivity tensor of symmetric anisotropic dielectric material. In a dielectric material case, the off‐diagonal elements of the matrix are symmetrical, i.e. ε r, xy= ε r, yx, and so forth. Similar expression can also be obtained for the symmetric anisotropic magnetic material. However, some media do not follow this symmetry rule.
To describe an anisotropic medium, two sets of the coordinate systems are used: one set is for the crystal structure axes of the anisotropic medium; and another set is used for the physical axes of the line structure. Figure (4.4)shows the crystal axes (ξ, η, ς), i.e. ( xi, eta, zeta ), and the physical axes (x, y, z) of a microstrip line on an anisotropic substrate.
The crystal axes (ξ, η, ς) are rotated with respect to the physical axes (x, y, z) by the angles θ 1, θ 2, and θ 3. The off‐diagonal elements of [ε r] in equation (4.2.4)are present due to the nonalignment of two coordinate systems. However, if they are aligned, i.e. θ 1= θ 2= θ 3= 0, then the off‐diagonal elements of [ε r] are zero; and the constitutive relation (4.2.4a)reduces to
(4.2.7) 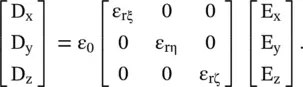
The crystal axes (ξ, η, ς) are also known as the principal coordinate system of a material medium; and the diagonal relative permittivity components ε rξ, ε rηand ε rζare known as the principal relative permittivity components [B.1, B.3, B.10, B.12–B.14, B.24]. Normally, all relative permittivity components are positive quantities. However, it is possible to get one component as a negative quantity in the engineered composites that provide unique EM‐wave characteristics [J.1, J.2, B.16]. Along the principal axes, the components of the vector 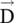 are parallel to vector
are parallel to vector 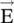 .
.
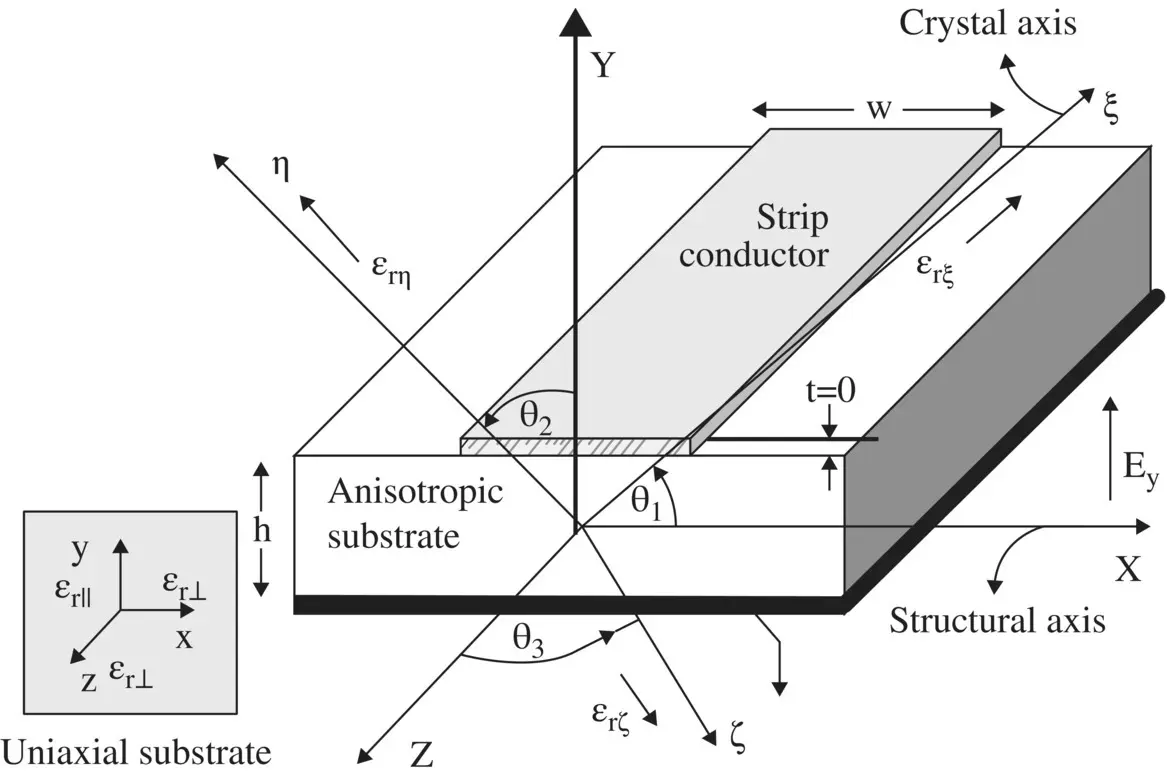
Figure 4.4 The crystal axes (ξ, η, ς) and the physical axes (x, y, z) of a planar anisotropic sheet.
The dielectric materials are further classified into three categories:
Type I: Isotropic materials . The relative permittivity components of these materials are identical, i.e. ε rζ= ε rη= ε rζ. Thus, the relative permittivity of isotropic material is a scalar quantity.
Type II: Uniaxial materials . These are anisotropic materials with relative permittivity components ε rζ= ε rξ= ε r⊥, and ε rη= ε r‖. It is shown within a box in Fig. (4.4). In the case of alignment of crystal axes along the physical axes, permittivity components are expressed as ε xx= ε zz= ε r⊥, ε yy= ε r‖. Thus, the permittivity tensor of the uniaxial anisotropic substrate is expressed as follows
(4.2.8) 
For a uniaxial substrate, shown in Fig. (4.4), the applied external electric field E yfaces the relative permittivity component ε r‖. The permittivity component ε r‖is parallel (||) to the normal (y‐axis) of an anisotropic substrate surface located in the (x‐z) plane. In the (x‐z) plane, the remaining two relative permittivity components have identical values ε r⊥. The relative permittivity components ε r⊥are in the plane normal (⊥) to the y‐axis, and also normal to the external electric field E y. The y‐axis is the main axis. It is also known as the C‐axis, or the optic‐axis, or the extraordinary axis . In the direction of the optic axis, the permittivity is different. The other two x‐ and z‐axes are known as the ordinary axes . The x‐ and z‐polarized EM‐waves, known as the ordinary waves , in the (x‐z)‐plane travel with the same velocity, whereas y‐polarized EM‐wave, known as the extraordinary wave, travels with another velocity. The nonhomogeneous medium as shown in Fig. (4.3) is also a uniaxial medium with the x‐axis as the optic axis, supporting the extraordinary wave propagation. The y and z‐axes are the ordinary axes, supporting the ordinary wave propagation.
Figure (4.4)shows a microstrip line of width w on an anisotropic substrate of thickness h. It forms a parallel‐plate capacitor placed in the (x‐z)‐plane. It views ε r‖component of the uniaxial relative permittivity. Whereas, if the parallel plates of the capacitor are placed either in the (x‐y)‐plane or the (y‐z)‐plane, it will view the ε r⊥component of a uniaxial substrate medium. Thus, a uniaxial dielectric medium offers two different values of capacitance, depending on the placement of the parallel plates, connected to a voltage source. Normally, manufacturers provide data for ε r‖and ε r⊥of the uniaxial substrates. The constitutive relation for the uniaxial medium aligned to the physical axes is
(4.2.9) 
In the case of the crystal axes ξ, η of an anisotropic substrate, shown in Fig. (4.4), have an angle θ = θ 1= θ 2with respect to the physical axes x, y; the relative permittivity components could be computed by the following expressions [B.24]:
(4.2.10) 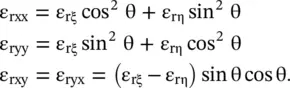
Type III: Biaxial materials . For such an anisotropic medium, all three principal relative permittivity components are different, i.e. ε rξ≠ ε rη≠ ε rζ. Such a medium is known as the biaxial medium [B.3].
The above nomenclatures are also applicable to the permeability of a magnetic material.
Anti‐symmetric Anisotropic Materials
The plasma medium, i.e. the electron gas model of metal or ionosphere, is treated as an isotropic medium. However, in the presence of a static biasing magnetic field, it becomes a uniaxial dielectric material with off‐diagonal elements for the permittivity matrix. This permittivity matrix is anti‐symmetric. It does not support linearly polarized characteristic waves as the normal modes. It forms a gyroelectric medium, i.e. electrically gyrotropic medium . Similarly, in the presence of a static biased magnetic field in the z‐direction, ferrite medium becomes a gyromagnetic medium, i.e. magnetically gyrotropic medium . Both plasma and ferrite media, under the magnetic biasing, support propagation of circularly polarized characteristic waves as the normal modes [B.2–B.4, B.21, B.22]. The permittivity and permeability tensors in matrix form for these media are summarized below.
Читать дальше

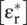 , showing the permittivity tensor, of symmetric anisotropic dielectric material is a Hermitian symmetric matrix, i.e. the following relation holds:
, showing the permittivity tensor, of symmetric anisotropic dielectric material is a Hermitian symmetric matrix, i.e. the following relation holds: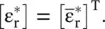
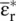 are the complex conjugate of the matrix elements
are the complex conjugate of the matrix elements 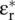 . The superscript T shows the transpose of the permittivity matrix. The above relation also holds for a real permittivity tensor of symmetric anisotropic dielectric material. In a dielectric material case, the off‐diagonal elements of the matrix are symmetrical, i.e. ε r, xy= ε r, yx, and so forth. Similar expression can also be obtained for the symmetric anisotropic magnetic material. However, some media do not follow this symmetry rule.
. The superscript T shows the transpose of the permittivity matrix. The above relation also holds for a real permittivity tensor of symmetric anisotropic dielectric material. In a dielectric material case, the off‐diagonal elements of the matrix are symmetrical, i.e. ε r, xy= ε r, yx, and so forth. Similar expression can also be obtained for the symmetric anisotropic magnetic material. However, some media do not follow this symmetry rule.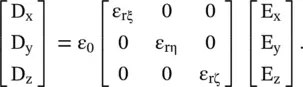
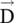 are parallel to vector
are parallel to vector 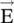 .
.