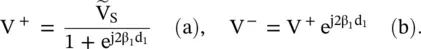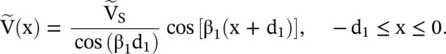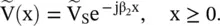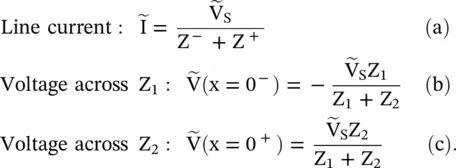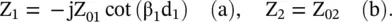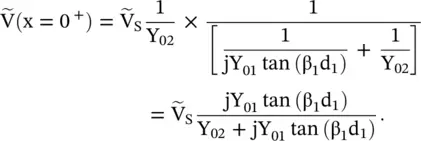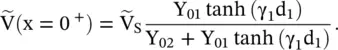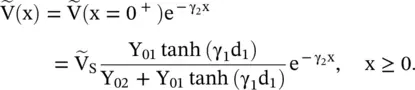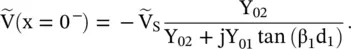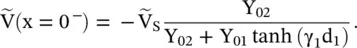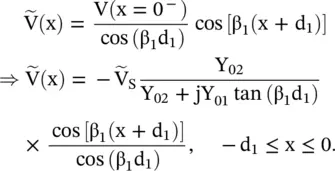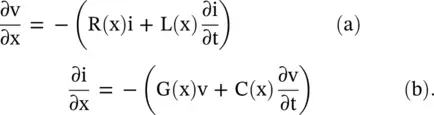(2.2.15) 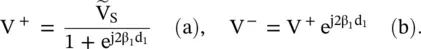
The voltage wave on the left‐hand line #1 is obtained by substituting equation (2.2.15)in equation (2.1.79a):
(2.2.16) 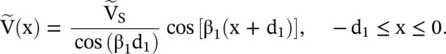
The line at the right‐hand side of the current source is an infinite length line that supports a traveling wave without any reflection. Therefore, at x = 0, V −= 0 and V += V S. The voltage wave on line #2 at the right‐hand side is
(2.2.17) 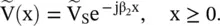
The method can be easily extended to a multisection line structure. For this purpose, the left‐hand and right‐hand side admittances Y −and Y +are determined at the plane containing the current source.
Figure (2.12a)shows the series‐connected voltage source V Sat x = 0. The location x = 0 is a junction of two transmission lines – line #1 open‐circuited finite‐length line and line #2 infinite length line. The lines at the left‐hand and right‐hand sides of the voltage source can be replaced by the equivalent impedances Z −and Z +, respectively. It is shown in the equivalent circuit, Fig (2.12b). Again, the voltage waves on both lines, excited by a series voltage source, could be determined.
The voltages across loads Z −(Z 1) and Z +(Z 2), shown in Fig (2.12b), are obtained as follows:
(2.2.18) 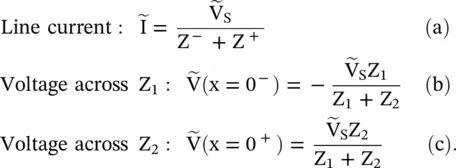
Line #1 is open‐circuited and line #2 is of infinite extent. Therefore, their input impedances at x = 0 −and x = 0 +are
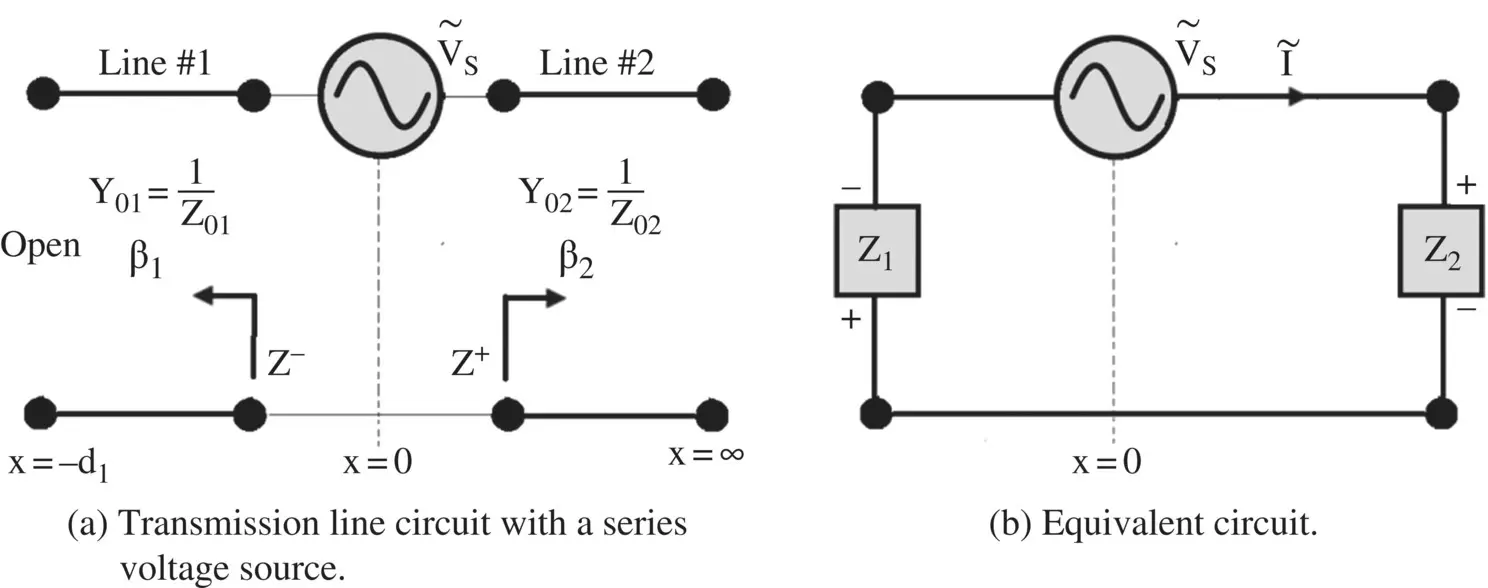
Figure 2.12 A series voltage source at the junction of two‐line sections.
(2 2 19) 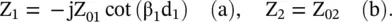
The voltage at x = 0 +from equations (2.2.18c)and (2.2.19)is
(2.2.20) 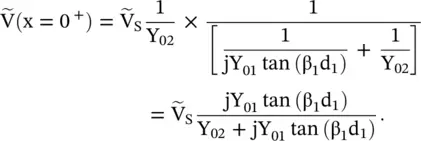
For a lossy transmission line, the above equation could be written as follows:
(2.1.21) 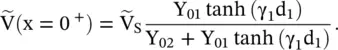
The voltage wave on the infinite extent lossy line #2 is
(2.2.22) 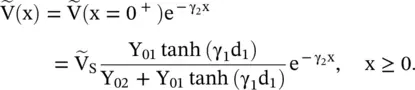
The voltage at x = 0 −on the lossless line #1 is
(2.2.23) 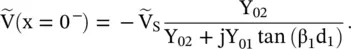
However, the voltage at x = 0 −on a lossy line #1 is
(2.2.24) 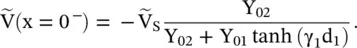
The voltage wave on the open‐circuited lossless line #1 is obtained from equations (2.2.16)and (2.2.23):
(2.2.25) 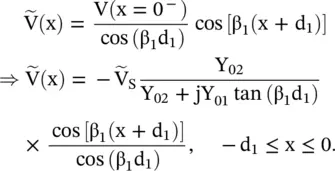
2.3 Nonuniform Transmission Lines
The previous sections have presented the voltage and current waves on the uniform transmission line that has no change in the geometry along the direction of propagation. For a uniform line, the relative permittivity and relative permeability also do not change along the line. For such a uniform lossless or low‐loss transmission line, the voltage and current waves travel at a definite velocity from low frequency to high frequency. The uniform transmission line behaves as a low‐pass filter (LPF) section. The propagation constant for such a uniform transmission line is the same at any section of the line. The line also has a unique characteristic impedance that is independent of the location on a line. However, if the geometry of a transmission line or an electrical property of the medium of a line changes in the direction of propagation, such a line is no longer a uniform transmission line. It is a nonuniform transmission line . Its electrical properties, such as the RLCG primary constants, propagation constant, phase velocity, and characteristic impedance, become a function of the space coordinate along the direction of propagation. The characteristic impedance of a nonuniform transmission line changes from one end to another end; therefore, it finds application in the broadband impedance matching [B.9, B.10, B.12]. It is also used for the design of delay equalizers, filters, wave‐shaping circuits, etc. [J.6–J.9]. It is an essential section of the on‐chip measurement system [J.10]. Unlike a uniform transmission line, it shows a cut‐off phenomenon, i.e. the wave propagates on the line only above the cut‐off frequency . Below the cut‐off frequency, the wave only attenuates with distance. Thus, the nonuniform transmission line behaves like a high‐pass filter (HPF) section [J.11–J.13, B.17].
The present section obtains the wave equations for a nonuniform transmission line. However, like the uniform transmission lines, the nonuniform transmission lines do not have closed‐form solutions for the voltage and current waves. The numerical methods have been used to determine the response of an arbitrarily shaped nonuniform transmission line [J.10, J.11]. However, this section discusses only the exponential nonuniform transmission line to understand its characteristics.
2.3.1 Wave Equation for Nonuniform Transmission Line
Figure (2.13)shows a nonuniform transmission line. The line parameters (primary line constants) R(x), L(x), C(x), G(x) are distance‐dependent. It results in the distance‐dependent characteristic impedance, Z 0(x), and propagation constant, γ(x). Using equation (2.1.20), the voltage and current equations for a nonuniform transmission line are written as follows:
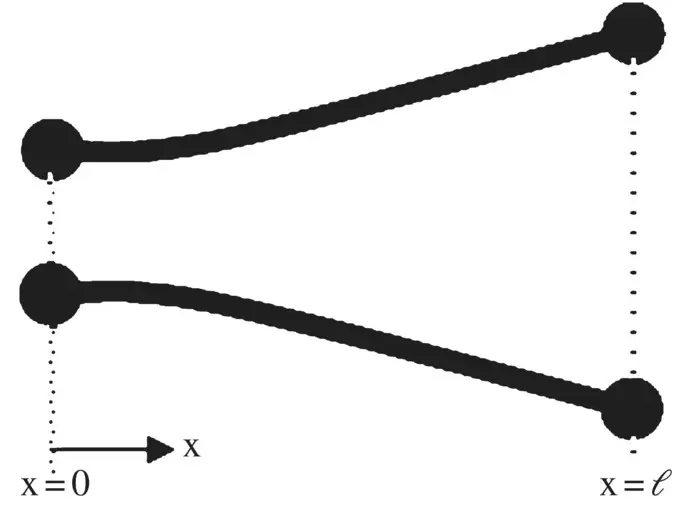
Figure 2.13 Nonuniform transmission line.
(2.3.1) 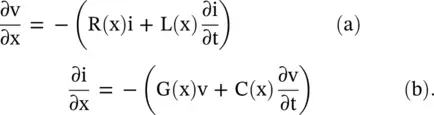
The following expressions are obtained on differentiating equation (2.3.1a)with x and equation (2.3.1b)with t:
Читать дальше