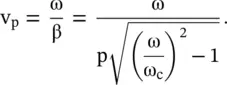The parameter p, defined below, could be determined from the characteristic impedance at the input and output ends of the line:
(2.3.18) 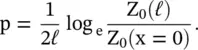
If the impedances at both ends of a line are fixed, changing the line length, ℓ, can change the parameter p. The parameter p also determines the propagation characteristics of a nonuniform transmission line. The series impedance and shunt admittance p.u.l . of the exponential line can be written as follows:
(2.3.19) 
In case of an exponential line, the voltage and current wave equations (2.3.9)and (2.3.10)reduce to
(2.3.20) 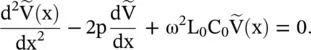
(2.3.21) 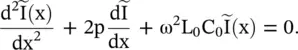
Let us assume the following exponential form of the solution for the above wave equations with separate propagation constants for the voltage and current waves:
(2.3.22) 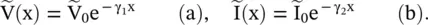
The above differential equations provide the following characteristic equations:
(2.3.23) 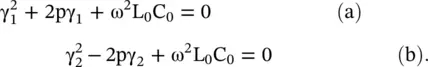
On solving the above equations, the following expressions are obtained for the complex propagation constants:
(2.3.24) 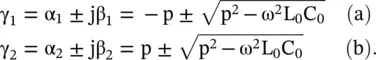
In the case of a uniform transmission line (p = 0), the propagation constants for the voltage and current waves are identical. The parameter p determines the attenuation constant, i.e. α of a nonuniform line. It is positive for the condition Z 0(x = ℓ) > Z 0(x = 0). Thus, there is an attenuation factor even for a lossless nonuniform line. The factor under the radical sign provides the propagation constant, i.e. the phase‐shift constant β. At the cut‐off frequency, ω = ω c, β is zero. The cut‐off frequency is given by
(2.3.25) 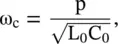
where phase velocity of the voltage and current waves on the line at x = 0 is
(2.3.26) 
The complex propagation constants can be rewritten as follows:
(2.3.27) 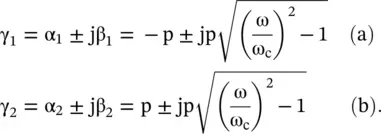
The propagation constants β 1and β 2are imaginary quantities for the signal below the cut‐off frequency ω < ω c. Under such conditions, no wave propagates on the nonuniform line. The initial signal only gets attenuated. It is called the evanescent mode . The wave propagation takes place only for ω > ω c. Therefore, a nonuniform transmission line behaves like a high‐pass filter (HPF). However, real parts of the complex propagation constants γ 1and γ 2are nonzero. For p > 0, the voltage wave gets attenuated while the current wave is increased in the positive direction of wave propagation. In the backward direction, the reflected voltage and current waves have opposite behavior. The attenuation in the signal is not due to any ohmic loss of a line. It is due to the continuous reflection of the wave as it progresses on the line. The opposite behavior of the voltage and current waves maintains the constant flow of power (P) at any location on a line:
(2.3.28) 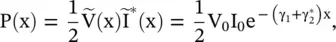
where 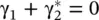 . Unlike a lossless uniform transmission line, the phase velocity of the voltage and current waves on a lossless nonuniform transmission line is dispersive as given below:
. Unlike a lossless uniform transmission line, the phase velocity of the voltage and current waves on a lossless nonuniform transmission line is dispersive as given below:
(2.3.29) 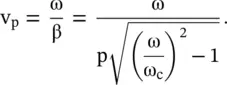
The phase velocity shows singularity at the cut‐off frequency. After the cut‐off frequency, i.e. for ω > > ω c, it decreases, with an increase in frequency, to a value given by expression (2.3.26).
1 B.1 Nahin Paul, J.: Oliver Heaviside, Sage in Solitude: The Life, Work, and Times of an Electrical Genius of the Victorian Age, IEEE Press, New York, 1988.
2 B.2 MacCluer, C.R.: Boundary Value Problems and Fourier Expansions, Dover Publications, Mineola, NY, 2004.
3 B.3 Sears, F.W.; Zemansky, M.W.: University Physics, Addition‐Wesley, Boston, MA, 1973.
4 B.4 Huygens, C.: Treatise on Light, Macmillan, London, 1912.
5 B.5 Karakash, J.J.: Transmission Lines and Filter Networks, Macmillan, New York, 1950.
6 B.6 Johnson, W.C. Transmission Lines and Networks, McGraw‐Hill, Inc., New York, 1950.
7 B.7 Mattick, R.E.: Transmission Lines for Digital and Communication Networks, IEEE Press, New York, 1995.
8 B.8 Weeks, W.L.: Electromagnetic Theory for Engineering Applications, John Wiley & Sons, New York, 1964.
9 B.9 Rizzi, P.A.: Microwave Engineering‐ Passive Circuits, Prentice‐Hall International Edition, Englewood Cliff, NJ, 1988.
10 B.10 Pozar, D.M.: Microwave Engineering, 2nd Edition, John Wiley & Sons, Singapore, 1999.
11 B.11 Ramo, S.; Whinnery, J.R.; Van Duzer, T.: Fields, and Waves in Communication Electronics, 3rd Edition, John Wiley & Sons, Singapore, 1994.
12 B.12 Collin, R.E.: Foundations for Microwave Engineering, 2nd Edition, McGraw‐Hill, Inc., New York, 1992.
13 B.13 Rao, N.N.: Elements of Engineering Electromagnetics, 3rd Edition, Prentice‐Hall, Englewood Cliff, NJ, 1991.
14 B.14 Sadiku, M.N.O.: Elements of Electromagnetics, 3rd Edition, Oxford University Press, New York, 2001.
15 B.15 Cheng, D.K.: Fields and Wave Electromagnetics, 2nd Edition, Pearson Education, Singapore, 1089.
16 B.16 Bhattacharyya, A.K.: Electromagnetic Fields in Multilayered Structures, Artech House, Norwood, MA, 1994.
17 B.17 Lewis, I.A.D.; Wells, F.H.: Millimicrosecond Pulse Techniques, 2nd Edition, Pergamon Press, London, 1939.
1 J.1 Searle, G.F.C., et al. The Heaviside Centenary Volume, The Institution of Electrical Engineers, London, 1950.
Читать дальше


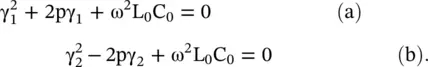
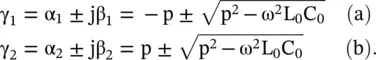
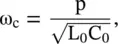

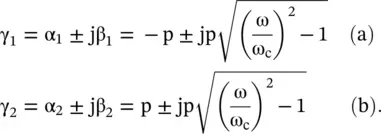
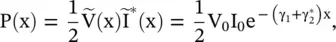
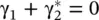 . Unlike a lossless uniform transmission line, the phase velocity of the voltage and current waves on a lossless nonuniform transmission line is dispersive as given below:
. Unlike a lossless uniform transmission line, the phase velocity of the voltage and current waves on a lossless nonuniform transmission line is dispersive as given below: