The input impedance of an infinite line at any location x is Z in(x) = Z 0. Thus, a finite line terminated in its characteristic impedance, i.e. Z L = Z 0 behaves as an infinite extent transmission line without any reflection . The characteristic impedance shows a specific feature of a line that is determined by the geometry and physical medium of the line. Once a finite extent line is terminated in any other load impedance, i.e. Z L≠ Z 0, the voltage and current waves are reflected from the load. The wave reflection is expressed by the reflection coefficient , Γ(x). The reflection coefficient is a complex quantity and its phase changes over the length of a line. However, its magnitude remains constant over the length of a lossless line. The interference of the forward‐moving and backward‐moving reflected waves produces the standing wave with maxima and minima of the voltage and current on a line. Figure (2.8c)shows the voltage standing wave. The position and magnitude of the voltage maxima V maxand voltage minima V minare measurable quantities. Their positions are measured from the load end. The reflection coefficient , and also the voltage standing wave ratio , VSWR, i.e. S, is defined using the V maxand V min. The VSWR could be measured with a VSWR meter. Therefore, the reflection on a transmission line is expressed by both the reflection coefficient and the VSWR. The reflection at the input terminal of a line is also expressed as the return‐loss , RL = − 20 log 10|Γ in|. The wave behavior in terms of the reflection parameter is an important quantity in the design of circuits and components in the microwave and RF engineering.
At the load end, the total line voltage is a sum of the forward and reflected waves, and it is equal to the voltage drop V Racross the load impedance Z L. It is shown in Fig (2.8a). To simplify expressions for the line voltage and current, the origin is shifted from the source end to the load end. In that case, expressions for both the line voltage and line current, given by equation (2.1.79), have to be modified for the new distance variable x < 0. Now the source and load are located at x = − ℓ and at x = 0, respectively. For the origin at the load end, the reflected wave V −e (ωt + γx)appears as the “forward‐traveling wave” from load to the source, whereas the wave incident at the load V +e (ωt − γx)appears as the “backward‐traveling” wave. The voltage drop across the load is
(2.1.83) 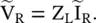
Keeping in view that the origin of the distance (x = 0) is at the load, the line voltage and current at the load end are written, from equation (2.1.79), as follows:
(2.1.84) 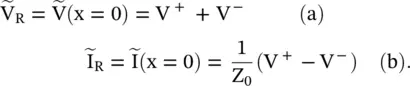
The voltage reflection coefficient at the load end is defined as follows:
(2.1.85) 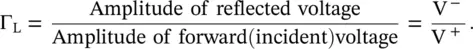
The expression to compute the reflection coefficient at the load end is obtained from the above equations (2.1.83) – (2.1.85): equations:
(2.1.86) 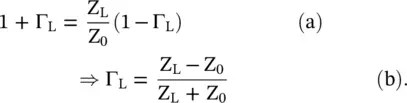
The mismatch of a load impedance Z Lwith the characteristic impedance Z 0of a line is the cause of the reflection at the load end. For the condition Z L= Z 0, the matched load terminated line avoids the reflection on a line, as Γ L= 0. At any distance x, the reflection coefficient is a complex quantity with both the magnitude and phase expressed as follows:
(2.1.87) 
A lossless line has |Γ(x)| = |Γ L|, i.e. on a lossless line magnitude of the reflection is the same at all locations on a line. However, the lagging phase ϕ changes with distance. It has 180° periodicity, i.e. for an inductive load, the range of phase is 0 < ϕ < π, and a capacitive load has the phase in the range −π < ϕ < 0. Using equation (2.1.79), the line voltage and line current are written in term of the load reflection coefficient:
(2.1.88) 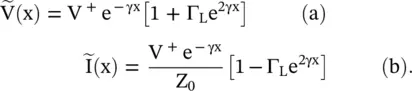
For a lossless transmission line, the above equations are written as follows:
(2.1.89) 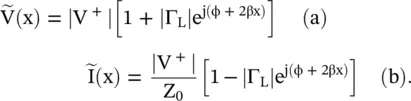
In the above equations, the origin is at the load end, i.e. x < 0. The maxima and minima of the voltage and current waves along the line occur due to the phase variation along the line. The voltage maximum occurs at e j(ϕ + 2βx)= + 1. In this case, both the forward and reflected waves are in‐phase. The voltage minimum occurs at e j(ϕ + 2βx)= − 1. In this case, both the forward and reflected waves are out of phase. Finally, the maxima and minima of the voltage on a line are given as follows:
(2.1.90) 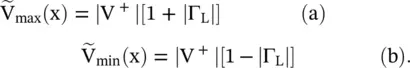
The reflection coefficient Γ(x) at any location x from the load end is related to the reflection coefficient at the load Γ Lby
(2.1.91) 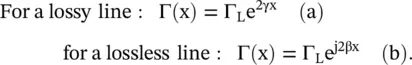
The measurable quantity voltage standing wave ratio (VSWR) is defined as follows:
(2.1.92) 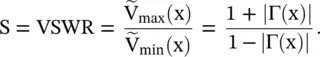
For a lossless line, the VSWR is constant along the length of a line . Likewise, the current standing wave ratio is also defined.
The wave reflection also takes place at the sending end when the source impedance Z gis not matched to the characteristic impedance of a line. The reflection coefficient at x = − ℓ, i.e. at the generator (source) end is defined as Γ(x = − ℓ) = Γ g. The voltage and current at the generator end are obtained from equation (2.1.88),
(2.1.93) 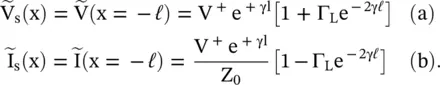
The amplitude factor V +is determined by the reflections at both the source and load ends.
Figure (2.8b)shows that the port voltage 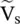 and the line current
and the line current 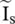 , at the input port – aa, are related to the source voltage
, at the input port – aa, are related to the source voltage 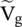 and its internal impedance Z gby
and its internal impedance Z gby
Читать дальше

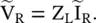
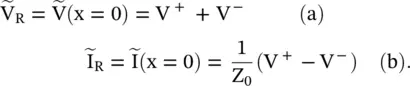
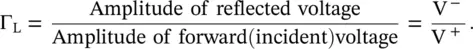
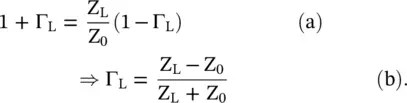

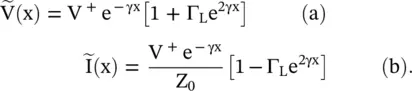
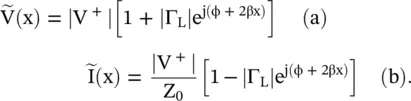
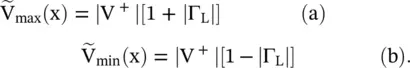
 and the line current
and the line current 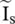 , at the input port – aa, are related to the source voltage
, at the input port – aa, are related to the source voltage 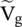 and its internal impedance Z gby
and its internal impedance Z gby










