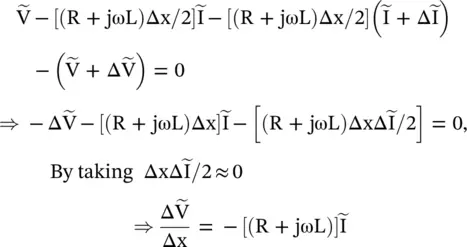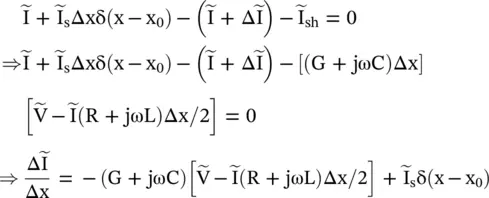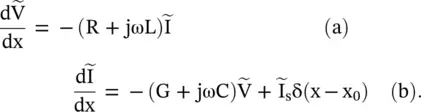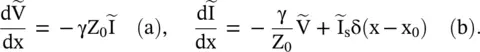(2.1.45) 
(2.1.46) 
(2.1.47) 
In the above expression, ω 3and ω 4terms are neglected. If we neglect ω 2terms and also take G = 0 or R = 0, equation (2.1.47)reduces to either equation (2.1.43)or equation (2.1.44), respectively. It is also possible that with the change of frequency, the imaginary part of characteristic impedance changes from a positive to a negative value indicating that the dominant loss can change from the dielectric loss to the conductor loss. For such cases, R and G are usually frequency‐dependent [J.4]. Over a band of frequencies, the imaginary part of the characteristic impedance could be zero leading to
(2.1.48) 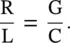
It is well known as Heaviside's condition . On meeting it, a lossy line becomes dispersion‐less and the propagation constant β becomes a linear function of frequency, while the attenuation constant becomes frequency‐independent. Following the above equation ( 2.1.48), a lossy line could be made dispersionless by the inductive loading [B.5, B.6].
The propagation constant γ of a uniform lossy transmission line is given by equation (2.1.34). It could be approximated under the low‐loss condition. Its real and imaginary parts are separated to get the frequently used approximate expressions for the attenuation and phase constants of a line:
(2.1.49) 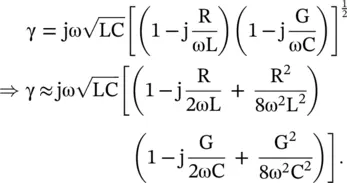
On neglecting ω 2, ω 3, and ω 4terms, the real part of the propagation constant γ provides the attenuation constant, whereas the imaginary part gives the propagation constant:
(2.1.50) 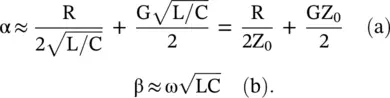
The first term of the above equation (2.1.50a) shows the conductor loss of a line, while the second term shows its dielectric loss. If R and G are frequency‐independent, the attenuation in a line would be frequency‐independent under ωL >> R and ωC >> G conditions. However, usually, R is frequency‐dependent due to the skin effect. In some cases, G could also be frequency‐dependent [B.7].
The dispersive phase constant β is obtained from the imaginary part of equation (2.1.49):
(2.1.51) 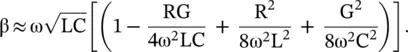
On neglecting the second‐order term, β becomes a linear function of frequency and the line is dispersionless. In that case, its phase velocity is also independent of frequency. A lossy line is dispersive. However, it also becomes dispersionless under the Heaviside's condition – (2.1.48 ). A transmission line, such as a microstrip in the inhomogeneous medium, can have dispersion even without losses.
2.1.6 Wave Equation with Source
In the above discussion, the development of the voltage and current wave equations has ignored the voltage or current source. However, a voltage or current source is always required to launch the voltage and current waves on a line. Therefore, it is appropriate to develop the transmission line equation with a source [B.8]. The consideration of a voltage/current source is important to solve the electromagnetic field problems of the layered medium planar lines, discussed in chapters 14and 16.
Figure (2.7)shows the lumped element model of a transmission line section of length Δx with a shunt current source 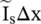 located at x = x 0. It is expressed through Dirac's delta function as
located at x = x 0. It is expressed through Dirac's delta function as 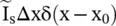 . The lumped line constants R, L, C, G are given for p.u.l .
. The lumped line constants R, L, C, G are given for p.u.l .
The loop and node equations are written below to develop the Kelvin–Heaviside transmission line equations with a current source:
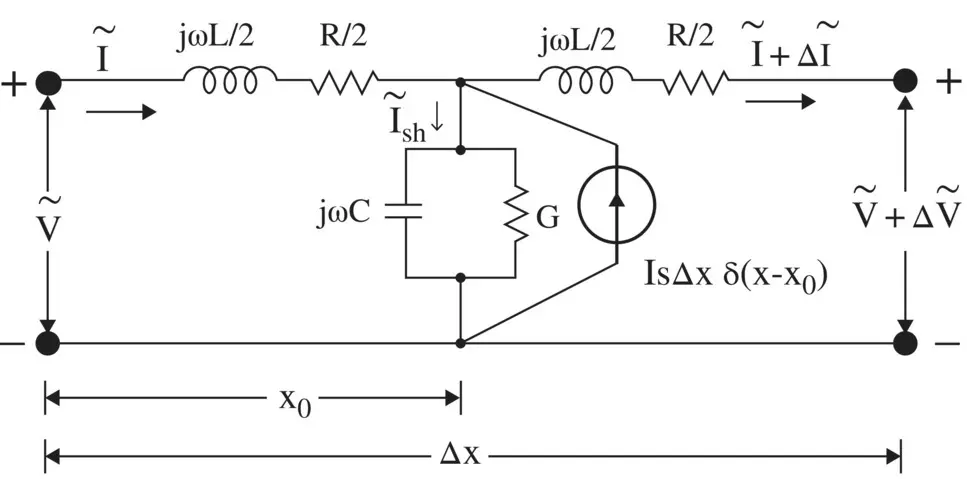
Figure 2.7 Equivalent lumped circuit of a transmission line with a shunt current source.
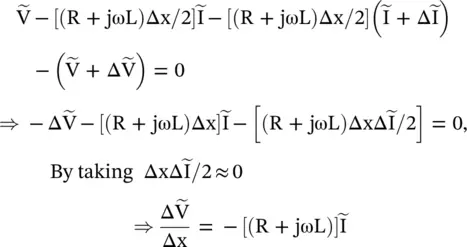
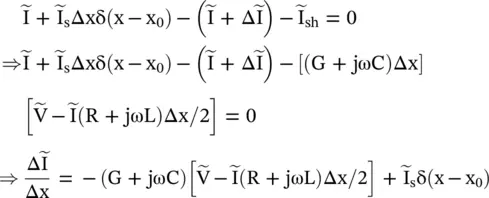
For Δx → 0, the above equations are reduced to
(2.1.52) 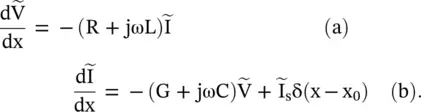
The above equations are rewritten below in term of the characteristic impedance (Z 0) and propagation constant (γ) of a transmission line:
(2.1.53) 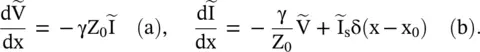
On solving the above equations for the voltage, the following inhomogeneous voltage wave equation, with a current source, is obtained:
(2.1.54) 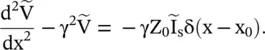
Away from the location of the current source, i.e. for x ≠ x 0, equation (2.1.54)reduces to the homogeneous equation (2.1.37a). The wave equation for the current wave, with a shunt current source, could also be rewritten.
2.1.7 Solution of Voltage and Current‐Wave Equation
The voltage and current wave equations in the phasor form are given in equation (2.1.37). The solution of a wave equation is written either in terms of the hyperbolic functions or in terms of the exponential functions. The first form is suitable for a line terminated in an arbitrary load. A section of the line transforms the load impedance into the input impedance at any location on the line. The impedance transformation takes place due to the standing wave formation. The hyperbolic form of the solution also provides the voltage and current distributions along the line. The exponential form of the solution demonstrates the traveling waves on a line, both in the forward and in the backward directions. A combination of the forward‐moving and the backward‐moving waves produces the standing wave on a transmission line.
Читать дальше

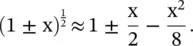
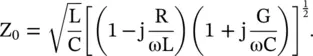
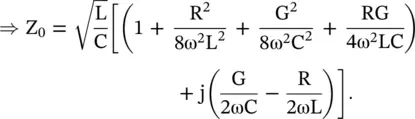
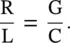
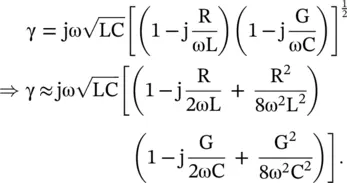
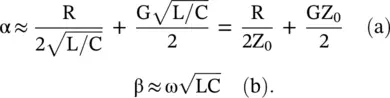
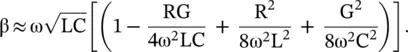
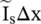 located at x = x 0. It is expressed through Dirac's delta function as
located at x = x 0. It is expressed through Dirac's delta function as 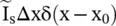 . The lumped line constants R, L, C, G are given for p.u.l .
. The lumped line constants R, L, C, G are given for p.u.l .