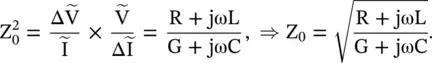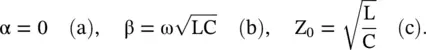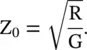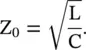(2.1.37) 
The above homogeneous wave equations on a transmission line could be treated as a boundary value problem to get the voltage and current at any location on the line. If a transmission line is infinitely long and excited from one end, then the voltage and current waves on the line always move in the forward direction without any reflection. At any location on the line, the voltage and current are related by another secondary parameter called “ the characteristic impedance ” of a transmission line:
(2.1.38) 
The characteristic impedance of a transmission line could be viewed as a mechanism that explains the wave propagation on a line. It recasts the Huygens' Principle of the secondary wave formation in terms of the characteristic impedance. The characteristic impedance could be called the Huygens' load . It is an unusual load impedance with a special property. It absorbs power from the source and itself becomes a secondary source for the further transmission of power in the form of wave motion. In this manner, the wave on a transmission line moves; as the characteristic impedance, i.e. Huygens' load, acts both as a load and also as a source of the wave motion. The process is similar to the Huygens' secondary source for the wavefront propagation. The concept of the Huygens' load is further extended to engineer the Huygens' metasurface with unique characteristics to control the reflected and transmitted (refracted) EM‐waves. It is discussed in subsection (22.5.2) of chapter 22.
The characteristic impedance, i.e. Huygens' load of a lossy line is a complex quantity. Its real part does not dissipate energy like the real part of a normal complex load. The imaginary part of Huygens's load indicates the presence of losses in a transmission line, whereas in the case of a normal complex load its imaginary part shows the storage of the reactive energy. For a lossless transmission line, Huygens' load is a real quantity 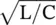 that is nondissipative. Huygens adopted the secondary source model to explain the propagation of the light wave in the space [B.3, B.4]. The expression for the characteristic impedance of a line is obtained from equation (2.1.32).
that is nondissipative. Huygens adopted the secondary source model to explain the propagation of the light wave in the space [B.3, B.4]. The expression for the characteristic impedance of a line is obtained from equation (2.1.32).
(2.1.39) 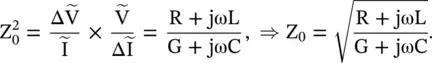
In general, the characteristic impedance of a lossy transmission line is a complex quantity. However, for a lossless line, the lossy elements are zero, i.e. R = G = 0. It leads to the following expressions:
(2.1.40) 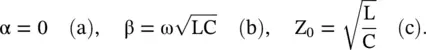
There is no attenuation in the propagating wave on a lossless line. If the line inductance L and the line capacitance C are frequency‐independent, the transmission line is nondispersive. The characteristic impedance is a real quantity. The line parameters such as the attenuation constant (α), propagation constant (β), and characteristic impedance (Z 0) are known as the secondary parameters of a transmission line. These secondary parameters are finally expressed in terms of the physical geometry and the electrical characteristics of material medium of a line. A microwave circuit designer is more interested in these secondary parameters as compared to the primary line constants, RLCG, of a transmission line. The secondary parameters are more conveniently measured and numerically computed for a large class of the transmission line structures. For any practical transmission line, the losses are always present on a line.
2.1.5 Characteristic of Lossy Transmission Line
A transmission line, such as a coaxial cable, a flat cable, used in the computer, or a feeder to TV receiver, is embedded in a lossy dielectric medium. The loss in a dielectric medium is known as the dielectric loss of a transmission line. Of course, when the line is in the air medium, the dielectric loss could be neglected. Likewise, there is another kind of loss, known as the conductor loss, on a transmission line. It is due to the finite conductivity of the conducting wires or the strip conductors forming a line. All open transmission lines tend to radiate some power, leading to radiation loss . In the case of a planar transmission line, there are also other mechanisms of losses. However, this section considers only the conductor and the dielectric losses of a line and their effect on the propagation characteristics of the line.
The characteristic impedance Z 0of a uniform lossy transmission line is given by equation (2.1.39). In the limiting case, ω → 0, i.e. at a lower frequency, it is reduced to a real quantity that is dominated by the lossy elements of a line:
(2.1.41) 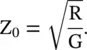
The characteristic impedance Z 0at very high frequency, i.e. for ω → ∞, is also reduced to a real quantity. However, now it is dominated by the lossless reactive elements:
(2.1.42) 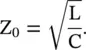
At higher frequency, we have ωL >> R and ωC >> G. Therefore, the R and G are normally ignored for the computation of characteristic impedance of a low‐loss microwave transmission line. In the intermediate frequency range, the characteristic impedance of a line is a complex quantity. Its imaginary part indicates the presence of the loss in a line. Equation (2.1.42)is also applicable to a lossless line.
The characteristic impedance of transmission line in the lossless dielectric medium, or a moderately lossy medium where G could be neglected, is obtained in equation (2.1.43). However, the conductor loss is present on the line:
(2.1.43) 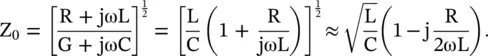
The measured or computed complex characteristic impedance of a line, over a certain frequency range, with a negative imaginary part, indicates that the loss in the line is mainly due to the conductor loss [J.4].
The alternative case of a lossy line, with G ≠ 0, R = 0, could be also considered. In this case, the conductor loss is ignored; however, the dielectric loss is dominant. The characteristic impedance of such line is approximated as follows:
(2.1.44) 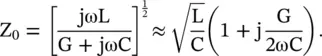
If the imaginary part of the characteristic impedance of a line is positive over some frequency range, then the dielectric loss dominates the loss in the line. However, if both R and G are moderately present, with ωL >> R and ωC >> G, the real and imaginary parts of the characteristic impedance could be approximated by using the binomial expansion as follows:
Читать дальше

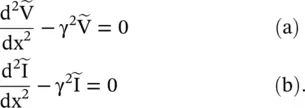
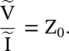
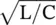 that is nondissipative. Huygens adopted the secondary source model to explain the propagation of the light wave in the space [B.3, B.4]. The expression for the characteristic impedance of a line is obtained from equation (2.1.32).
that is nondissipative. Huygens adopted the secondary source model to explain the propagation of the light wave in the space [B.3, B.4]. The expression for the characteristic impedance of a line is obtained from equation (2.1.32).