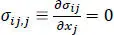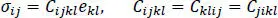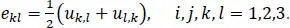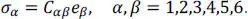Modern Trends in Structural and Solid Mechanics 1

Composites are being increasingly used in transportation, aviation and defense industries because of their high specific strength and our ability to tailor their elastic moduli and ultimate strengths in desired directions and at critical locations in the structure. They are usually in the form of a laminate composed of numerous plies, with each ply having unidirectional fibers. The volume fraction of fibers in different plies can be varied to suit the intended application. Recognizing that design is an iterative process, it is imperative that we can easily and accurately analyze a structure’s response to external stimuli.

Closed-form solutions for three-dimensional linear elasticity equations for composite laminates are scarce. Assuming that the Euler–Bernoulli beam theory applies to a composite laminated beam and the Kirchhoff–Love theory is relevant for a composite laminated plate, enables us to analytically solve some boundary value problems (see, for example, Jones (1998) and Hyer (2009)). Elishakoff has reviewed various theories for plates and laminates and has provided their historical perspective (Elishakoff 2018). However, for general structures, we resort to numerical methods for solving the governing equations.

A challenge in solving problems for laminates is accurately finding transverse stresses that can cause delamination between adjacent plies. For simply supported edges, the linear elasticity equations have been solved by expressing the three displacements as double Fourier series in the in-plane coordinates and deducing ordinary differential equations for them in the thickness direction (Vlasov 1957; Pagano 1969; Srinivas and Rao 1970). For other boundary conditions at the edges, Vel and Batra employed the Eshelby–Stroh formalism and satisfied boundary conditions at the edges in the sense of Fourier series (Vel and Batra 1999; Vel and Batra 2000) that rely on St. Venant’s principle. This principle states that the solution at points away from the edges is unaffected by the boundary conditions, provided that they are equipollent to the same resultant force and moment (Toupin 1965). The distance from the edges, usually called the decay length, where the solution is unaffected, depends on the lowest frequency of free vibrations of a slice of the structure of characteristic length l and the maximum eigenvalue of the elasticity matrix. For composite laminates, the decay length has been estimated in Horgan and Baxter (1998).

A common approach, called the state space method, is to take the three transverse stresses and the three displacements as variables, cast governing equations for them as first-order partial differential equations (PDEs) in the thickness coordinate, z, and find their values simultaneously. The boundary value problem is thus reduced to one that looks like an initial value problem. One way to solve these PDEs is to find a propagation matrix that relates variables for two different values of z (see, for example, Bahar (1975)). Kant and Ramesh have presented Goldberg and Bogdanoff’s method of numerically solving these six first-order equations (Goldberg and Bogdanoff 1957; Kant and Ramesh 1981) that satisfy the prescribed boundary conditions at the top and the bottom surfaces of a plate. Here, we also solve for the three in-plane strains, along with the aforementioned six unknowns, use the least-squares method, polynomial basis functions of possibly different orders in each one of the three directions defined on the entire structure’s domain, include in the functional to be minimized boundary conditions at the six edges of a laminate and derive a set of simultaneous algebraic equations; see, for example, Moleiro et al . (2011) who have analyzed numerous problems. The contribution of this work is in demonstrating that polynomial basis functions defined on the entire domain enable us to find a reasonably accurate solution of the linear elasticity equations, for rectangular composite laminates of side length equal to twice the thickness and sandwich structures with the ratio of the axial elastic modulus of a facesheet to that of the core less than 1000.

The rest of the chapter is organized as follows. The problem formulation is described in section 1.2. In section 1.3, the developed algorithm is verified by comparing predictions from it with the analytical solutions for a simply supported four-layer laminate and a sandwich structure, which also has results for a three-layer laminate with two opposite edges simply supported and the other two edges either free or clamped. Significant outcomes of the work are briefly summarized as conclusions.

We formulate the problem for a rectangular a x b x h lamina that can be easily extended to a laminate made of p layers. We employ rectangular Cartesian coordinates (x 1, x 2, x 3), shown in Figure 1.1, to describe the position of a material particle in the unstressed reference configuration. In the absence of body forces, infinitesimal deformations of the lamina are governed by the following equilibrium equations [1.1], stress–strain relations [1.2]and strain–displacement relations [1.3]:

[1.1]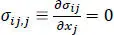

[1.2]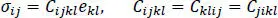

[1.3]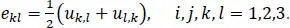

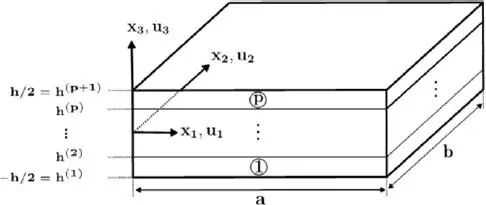
Figure 1.1. Geometry and coordinate-axes of a laminated plate

In equations [1.1]– [1.3], σis the stress tensor, eis the infinitesimal strain tensor, uis the displacement vector and Cis the matrix of elasticities. Here, a layer is modeled as a transversely isotropic material with the axis of transverse isotropy along the fiber. A repeated index implies summation over the range of the index. The substitution from equation [1.3]into [1.2], and the result into equation [1.1]gives three second-order partial differential equations for the three displacement components that are to be solved under the prescribed boundary conditions of surface tractions on one part of the boundary and displacements on the other part. Of course, linearly independent components of uand the surface traction vector, f i= σ ijn j, can alternatively be prescribed at a point of the boundary. Here, n jis the jth component of the outward unit normal to the boundary.

As is often done, we use the Voigt notation to express σand eas six-dimensional vectors and write equation [1.2]as

[1.4]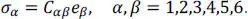

In equation [1.4], Cis a 6 x 6 symmetric matrix of elasticities of the layer material, and (σ 1,σ 2,σ 3,σ 4,σ 5,σ 6) = (σ 11,σ 22,σ 12,σ 13,σ 23,σ 33). A similar notation is used for e.

We use a mixed formulation and take s k= (u 1 k, u 2 k, u 3 k, σ 4 k, σ 5 k, σ 6 k, e 1 k, e 1 k, e 3 k) as unknowns at a point in each plate layer. In order to solve for sk, we define the following residuals on the k thlayer that only involve first-order derivatives for the elements of sk: