We used geoid coefficients from the GRACE geoid model GGM05 (Ries et al., 2016) and the hydrostatic correction from Chambat et al. (2010). We use a transdimensional, hierarchical, Bayesian approach to the inverse problem (e.g., Sambridge et al., 2013), based on the methodology described in (Rudolph et al., 2015). We carry out forward models of the geoid using the propagator matrix code HC (Hager and O’Connell, 1981; Becker et al., 2014). Relative to our previous related work (Rudolph et al., 2015), the inversions presented here differ in their treatment of uncertainty, scaling of velocity to density variations, and parameterization of radial viscosity variations.
Table 1.1 Summary of parameters used in geodynamic models. z lmdenotes the depth of the viscosity increase between the upper and lower mantle and Δ η lmis the magnitude of the viscosity increase at this depth. LVC indicates whether the model includes a low‐viscosity channel below 660 km. Spinup time is the duration for which the initial plate motions are imposed prior to the start of the time‐dependent plate model. We indicate whether the model includes the endothermic phase transition, which always occurs at a depth of 660 km and with Clapeyron slope –2 MPa/K.
| Case |
z lm |
Δ η lm |
LVC? |
Spinup time |
Phase transition? |
Start time |
| Case 8 |
660 km |
100 |
No |
150 Myr |
No |
400 Ma |
| Case 9 |
660 km |
30 |
No |
150 Myr |
No |
400 Ma |
| Case 18 |
1000 km |
100 |
No |
150 Myr |
Yes |
400 Ma |
| Case 32 |
660 km |
100 |
No |
150 Myr |
Yes |
400 Ma |
| Case 40 |
660 km |
100 |
Yes |
0 Myr |
Yes |
250 Ma |
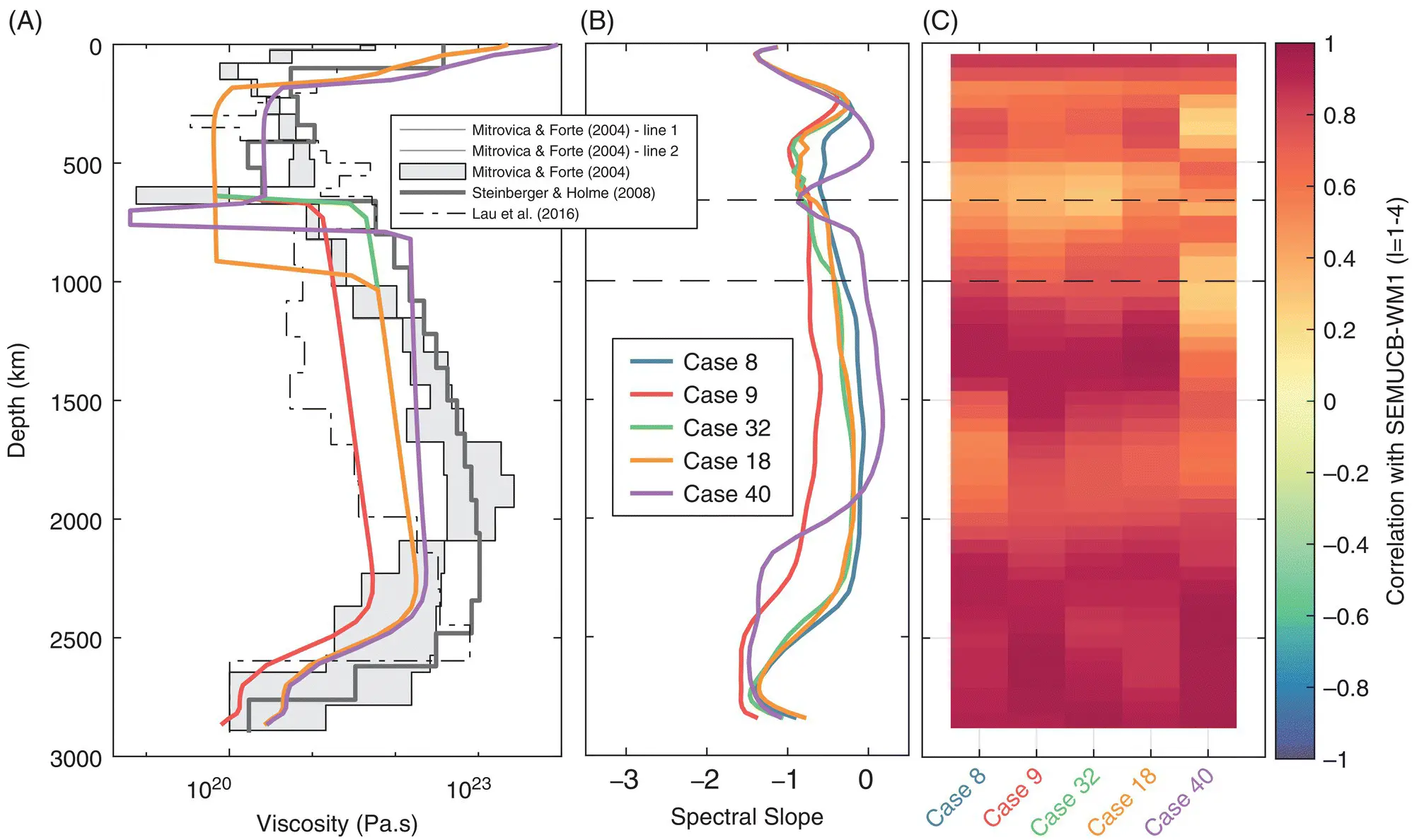
Figure 1.4 (A) Viscosity profiles used in our geodynamic models. For comparison, we also show viscosity profiles obtained in a joint inversion constrained by glacial isostatic adjustment (GIA) and convection‐related observables (Mitrovica and Forte (2004) Figure 1.4B), a combination of geoid, GIA, geodynamic constraints (Case C from Steinberger and Holme (2008)) and a joint inversion of GIA data including the Fennoscandian relaxation spectrum (Fig. 12 from Lau et al. (2016)). (B) Spectral slope vs. depth computed from the dimensionless temperature field of the geodynamic models. (C) Correlation at spherical harmonic degrees 1–4 between each of the geodynamic models and SEMUCB‐WM1.
We inferred density anomalies from two different tomographic models. First, we used SEMUCB‐WM1 and scaled Voigt V Sanomalies to density using a depth‐dependent scaling factor for a pyrolitic mantle composition along a 1600 K mantle adiabat, calculated from thermodynamic principles using HeFESTo Stixrude and Lithgow‐Bertelloni, 2011). Second, we used a whole‐mantle model of density variations constrained by full‐spectrum tomography (Moulik and Ekström, 2016). This model, hereafter referred to as ME16‐160, imposes a best data‐fitting scaling factor between density and V Svariations of d ln ρ / d ln V S= 0.3 throughout the mantle. We note that Moulik and Ekström (2016) present a suite of models with different choices for data weighting and preferred correlation between density variations and V Svariations in the lowermost mantle. The specific model used here ignores sensitivity to the density‐sensitive normal modes (data weight 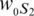 = 0) and imposes strong V S− ρ correlation in the lowermost mantle (
= 0) and imposes strong V S− ρ correlation in the lowermost mantle ( 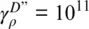 ). While this model is not preferred by seismic data, these choices produce a density model that closely resembles a scaled V Smodel in the lowermost mantle. We note that the assumption of purely thermal contributions to density is unlikely to be correct in the lowermost mantle, where temperature and compositional variations both contribute to density variations. However, this assumption should not affect our inferences of viscosity, for two reasons. First, previous viscosity inversions found that removing all buoyancy structure from the bottom 1,000 km of the mantle did not significantly influence the retrieved viscosity profile (Rudolph et al., 2015). This is confirmed by inversions for a four‐layer viscosity structure constrained by thermal vs. thermochemical mantle buoyancy Liu and Zhong (2016). Second, geodynamic models of thermochemical convection suggest that the thermal buoyancy above the LLSVPs counteracts the thermal and chemical buoyancy of the compositionally distinct LLSVPs, resulting in only a very small net contribution to the long‐wavelength geoid from the bottom 1,000 km of the mantle (Liu and Zhong, 2015).
). While this model is not preferred by seismic data, these choices produce a density model that closely resembles a scaled V Smodel in the lowermost mantle. We note that the assumption of purely thermal contributions to density is unlikely to be correct in the lowermost mantle, where temperature and compositional variations both contribute to density variations. However, this assumption should not affect our inferences of viscosity, for two reasons. First, previous viscosity inversions found that removing all buoyancy structure from the bottom 1,000 km of the mantle did not significantly influence the retrieved viscosity profile (Rudolph et al., 2015). This is confirmed by inversions for a four‐layer viscosity structure constrained by thermal vs. thermochemical mantle buoyancy Liu and Zhong (2016). Second, geodynamic models of thermochemical convection suggest that the thermal buoyancy above the LLSVPs counteracts the thermal and chemical buoyancy of the compositionally distinct LLSVPs, resulting in only a very small net contribution to the long‐wavelength geoid from the bottom 1,000 km of the mantle (Liu and Zhong, 2015).
In the inversions using SEMUCB‐WM1, we assume a diagonal covariance matrix to describe the data and forward modeling uncertainty on geoid coefficients, i.e., uncorrelated errors and uniform error variance at all spherical harmonic degrees (because the corresponding posterior covariance matrix is not available). For the inversions using ME16‐160, we first sample the a posteriori covariance matrix of the tomographic model, generating a collection of 10 5whole‐mantle models of density and wavespeed variations. For each of these models, we calculate a synthetic geoid assuming a reference viscosity profile (Model C from Steinberger and Holme (2008)). This procedure yields a sample of synthetic geoids from which we calculate a sample covariance matrix that is used to compute the Mahalanobis distance as a measure of viscosity model misfit.
In all of the inversions shown in this chapter, we include a hierarchical hyperparameter that scales the covariance matrix. This parameter has the effect of smoothing the misfit function in model space, and the value of the hyperparameter is retrieved during the inversion, along with the other model parameters. The inversion methodology, described completely in Rudolph et al. (2015), uses a reversible‐jump Markov‐Chain Monte Carlo (rjMCMC) method (Green, 1995) to determine the model parameters (the depths and viscosity values of control points describing the piecewise‐linear viscosity profile) and the noise hyperparameter (Malinverno, 2002; Malinverno and Briggs, 2004). The rjMCMC method inherently includes an Occam factor, which penalizes overparameterization. Adding model parameters must be justified by a significant reduction in misfit. The result is a parsimonious parameterization of viscosity that balances data fit against model complexity. In general, incorporating additional data constraints or a priori information about mantle properties could lead to more complex solutions.
The power spectra of four recent global tomographic models are shown in Figure 1.5. While S362ANI+M contains little power above spherical harmonic degree 20 due to its long‐wavelength lateral parameterization with 362 evenly spaced spline knots, the other models contain significant power at shorter wavelengths that are beyond the scope of this study. In general, the models are dominated by longer wavelengths at all depths. The spectral slope for each model (up to degree 20) is shown in the rightmost panel of Figure 1.5. Increasingly negative spectral slopes indicate that heterogeneity is dominated by long‐wavelength features. All of the models generally show a more negative spectral slope in the transition zone than in the upper mantle or the shallow lower mantle, indicating the presence of more long‐wavelength V Sheterogeneity within the transition zone and just below the 650 km discontinuity, which we attribute to the lateral deflection of slabs.
Читать дальше


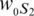 = 0) and imposes strong V S− ρ correlation in the lowermost mantle (
= 0) and imposes strong V S− ρ correlation in the lowermost mantle ( 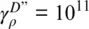 ). While this model is not preferred by seismic data, these choices produce a density model that closely resembles a scaled V Smodel in the lowermost mantle. We note that the assumption of purely thermal contributions to density is unlikely to be correct in the lowermost mantle, where temperature and compositional variations both contribute to density variations. However, this assumption should not affect our inferences of viscosity, for two reasons. First, previous viscosity inversions found that removing all buoyancy structure from the bottom 1,000 km of the mantle did not significantly influence the retrieved viscosity profile (Rudolph et al., 2015). This is confirmed by inversions for a four‐layer viscosity structure constrained by thermal vs. thermochemical mantle buoyancy Liu and Zhong (2016). Second, geodynamic models of thermochemical convection suggest that the thermal buoyancy above the LLSVPs counteracts the thermal and chemical buoyancy of the compositionally distinct LLSVPs, resulting in only a very small net contribution to the long‐wavelength geoid from the bottom 1,000 km of the mantle (Liu and Zhong, 2015).
). While this model is not preferred by seismic data, these choices produce a density model that closely resembles a scaled V Smodel in the lowermost mantle. We note that the assumption of purely thermal contributions to density is unlikely to be correct in the lowermost mantle, where temperature and compositional variations both contribute to density variations. However, this assumption should not affect our inferences of viscosity, for two reasons. First, previous viscosity inversions found that removing all buoyancy structure from the bottom 1,000 km of the mantle did not significantly influence the retrieved viscosity profile (Rudolph et al., 2015). This is confirmed by inversions for a four‐layer viscosity structure constrained by thermal vs. thermochemical mantle buoyancy Liu and Zhong (2016). Second, geodynamic models of thermochemical convection suggest that the thermal buoyancy above the LLSVPs counteracts the thermal and chemical buoyancy of the compositionally distinct LLSVPs, resulting in only a very small net contribution to the long‐wavelength geoid from the bottom 1,000 km of the mantle (Liu and Zhong, 2015).










