Hartmut Kuthan - Zufall im Leben der Zelle

ABBILDUNG 2: E. coli -Bakterien (elektronenmikroskopische Aufnahme).

Freilich dauerte es noch mehr als ein Jahrzehnt, bis fundierte Ergebnisse zunehmend an die Stelle von Vermutungen traten. Inzwischen ist unbestritten, dass nicht nur eukaryotische Zellen, sondern auch Bakterien eine komplexe, dynamische Organisation aufweisen. Darüber hinaus unterscheiden sich die Reaktionsbedingungen in Bakterienzellen fundamental von denen im Reagenzglas.

Im Folgenden werden wir auf einige grundlegende physikochemische Begriffe und Theorien eingehen, die für das Verständnis der molekularen Zellprozesse unentbehrlich sind, und die uns zum Leitthema des Buches – Stochastizität von Zellprozessen – zurückführen werden. Da ist zunächst der Begriff der Konzentration. Konzentrationen der Reaktionspartner erscheinen als unabhängige Variable in den kinetischen Gleichungen chemischer Reaktionen. Gleiches gilt für die Beschreibung des chemischen Gleichgewichts – auch hier gehen die Konzentrationen der Reaktionspartner ein, die üblicherweise in Mol pro Einheitsvolumen ausgedrückt werden. Ein Mol eines Stoffes enthält die gigantische Zahl von circa 6,022·10 23Atomen oder Molekülen, als Avogadro-Konstante bekannt, weshalb hier das Gesetz der großen Zahlen beziehungsweise Schrödingers „statistischer Mechanismus“ der Ordnung greift. Der gesetzmäßige Zusammenhang für das chemische Gleichgewicht wird als Massenwirkungsgesetz (MWG) bezeichnet; er wurde erstmals in den Jahren 1864 bis 1867 auf der Grundlage von kinetischen Überlegungen (Betrachtung der Hin- und Rückreaktionen) von dem Mathematiker Cato M. Guldberg (1836 - 1902) und seinem Schwager, dem Chemiker Peter Waage (1833 - 1900), formuliert, später von Josiah W. Gibbs (1839 - 1903) aus den thermodynamischen Potentialen für das chemische Gleichgewicht abgeleitet.31

Die klassischen Theorien der chemischen Kinetik und der phenomenologischen Thermodynamik, speziell das MWG, verkörpern den makroskopischen Determinismus; sie repräsentieren (nahezu) exakte Gesetze und ermöglichen genaue Voraussagen. So sind beispielsweise die das dynamische chemische Gleichgewicht charakterisierenden Konstanten durch den Quotienten der molaren Konzentrationen der Ausgangs- und Endprodukte gesetzmäßig festgelegt. Max Planck, der einen Großteil seiner aktiven wissenschaftlichen Laufbahn thermodynamischen Untersuchungen widmete, benutzte hierfür den Ausdruck Determinismus in der Molarwelt . Weiterhin konstatierte er, dass

Größenordnungsgebiete niemals durch scharfe Grenzlinien getrennt sind, sondern stets allmählich ineinander übergehen. Wir wissen aus der Kolloidchemie und aus der Biochemie, daß es unmöglich ist, molare und molekulare Vorgänge prinzipiell voneinander zu unterscheiden.32

Diese Feststellung wurde durch spätere biophysikalische Untersuchungen bestätigt: Zwischen die makroskopischen und mikroskopischen Systeme schiebt sich die, speziell für intrazelluläre Prozesse, äußerst bedeutsame „Mittelwelt“ der kleinen Systeme . Prozesse auf der physiologischen (interzellulären) Ebene, aber auch eine Reihe von intrazellulären Prozessen, sind im Rahmen des deterministischen Paradigmas beschreibbar. Doch sind es gerade die intrazellulären Kernprozesse, die als stochastisch erkannt wurden.

Den Gegenpol zu makroskopischen physikalischen oder chemischen Systemen, die durch deterministische Gesetze beschrieben werden, bilden mikroskopische Systeme. Mikroskopische Systeme sind Gegenstand der Quantenmechanik und der statistischen Physik. Und: Ereignisse in der Quantenwelt sind unbestimmt . Dagegen treten – wie durch Zauberei – infolge des Zusammenwirkens einer sehr großen Zahl von Atomen oder Molekülen Gesetzmäßigkeiten und Muster auf, gleichsam „Ordnung aus dem Chaos“. Die sich nach 1900 entwickelnde Theorie stochastischer Prozesse eröffnete noch eine weitere Möglichkeit, nämlich Systeme von „mittlerer Größe“ quantitativ zu beschreiben; hier liegt die Zahl der Moleküle weit unterhalb der Avogadro-Konstante, aber hoch genug, damit die Beschreibung durch Mittelwerte charakteristischer Systemeigenschaften möglich wird. Solche Systeme werden als klein oder mesoskopisch bezeichnet. In mesoskopischen Systemen treten Fluktuationen (Schwankungen) um die Mittelwerte in Erscheinung, die in makroskopischen Systemen wegen ihrer geringen Größe vernachlässigbar sind.33

Viele Prozesse der Zelle gehören zur „Mittelwelt“ mesoskopischer Größenordnung; sie laufen in Zellkompartimenten ab. Zu den Zellkompartimenten zählen unter anderem der Zellkern, die Mitochondrien, die umgrenzenden Membranen und das Zytoplasma. Zur „Mittelwelt“ gehören insbesondere auch die oben angeführten „molekularen Motoren“, die wesentlich für die Durchführung der vitalen Kernprozesse der Zelle sind.

Einen wegweisenden, wenngleich fast 20 Jahre unbeachtet gebliebenen, Beitrag zur stochastischen Kinetik veröffentlichte Max Delbrück im Jahre 1940; als Erster behandelte er die Fluktuationen einer biochemischen Reaktion – die autokatalytische Bildung von proteinspaltenden Enzymen (Proteasen) aus deren inaktiven Vorstufen, den Proenzymen. Diese Reaktion ist zugleich geeignet, Schrödingers „statistischen Mechanismus“, die Abnahme der relativen Fluktuationen mit der Quadratwurzel der Molekülzahl, zu veranschaulichen ( Abbildung 3 ).34

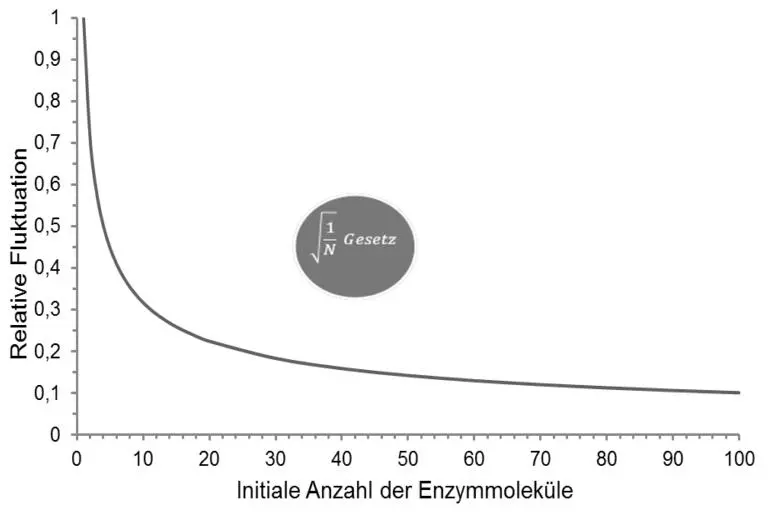
ABBILDUNG 3:Autokatalytische Umwandlung inaktiver Proenzymmoleküle in aktive Enzymmoleküle. Der Kurvenverlauf beschreibt das bekannte Quadratwurzel-Gesetz: die Abnahme der relativen Streuung (Variationskoeffizient) der Zahl gebildeter Enzymmoleküle mit zunehmender Anzahl der initial vorhandenen aktiven Moleküle – minimal ein Molekül. Hierbei wird angenommen, dass die Proenzymmoleküle in großem Überschuss vorliegen (Delbrück, 1940).

Die wahre Logik dieser Welt ist die Wahrscheinlichkeitsrechnung.

James Clerk Maxwell 1

Der stochastischen Behandlung biochemischer Reaktionen zeitlich weit voraus ging die theoretische Beschreibung und experimentelle Bestätigung einer der bedeutendsten molekularen Fluktuationserscheinungen – der Brown’schen Molekularbewegung.

Die Wärmebewegungen der Atome und Moleküle sind ein fundamentales physikalisches Phänomen. In Wasser suspendierte Partikel oder gelöste Moleküle erfahren in jeder Sekunde die unvorstellbar große Anzahl von 10 21Stößen durch die sie umgebenden Flüssigkeitsmoleküle. Sichtbaren Ausdruck finden diese Kollisionen in den andauernden, unregelmäßigen Bewegungen, welche die suspendierten Partikel ausführen. Die erratischen Partikelbewegungen werden nach dem Botaniker Robert Brown (1773 - 1858) als Brown’sche Bewegung bezeichnet.2 Auch die (Makro-)Moleküle und makromolekularen Komplexe der Zelle unterliegen diesem Schwankungsphänomen. Dies mag paradox erscheinen , stehen doch die Wärmebewegung und die aus ihr resultierende Brown’sche Molekularbewegung für Unordnung – Chaos und Zufall – schlechthin. Doch wir werden sehen, dass keine Zelle, kein Organismus ohne Brown’sche Bewegung existieren könnte, zumindest keine der derzeit bekannten, terrestrischen Lebensformen.