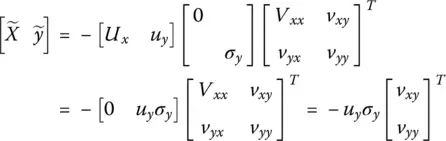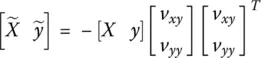Magdalena Salazar-Palma - Modern Characterization of Electromagnetic Systems and its Associated Metrology

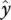The best approximation according to total least squares is that minimizes the norm of the difference between the approximated data and the model ( x ; a ) as well as the independent variables X . Considering the errors of the measured data vector, y , and the independent variables, X , (1.25)can be re‐written as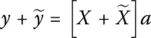

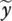(1.28)

where and 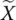are the errors in both the dependent variable measurements and independent variable measurements, respectively. We then want to approximate in a way that minimizes these errors in the dependent and independent variables. This can be expressed by,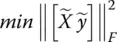

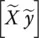(1.29)

where is an augmented matrix with the columns of error matrix 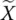concatenated with the error vector 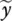. The operator ‖•‖ Frepresents the Frobenius norm of the augmented matrix. The Frobenius norm is defined as the square root of the sum of the absolute squares of all of the elements in a matrix. This can be expressed in equation form as the following, where A is any matrix,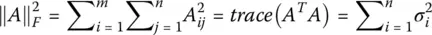

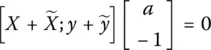
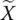(1.30)

and where σ iis the i ‐th singular value of matrix A .

We will now bring the right‐hand side of (1.28)over to the left side of the equation and equate it to zero as such

(1.31)

If the concatenated matrix [ X y ] has a rank of n + 1, the n + 1 columns of the matrix are linearly independent and the n + 1, m ‐dimensional columns of the matrix span the same n ‐dimensional space as X . In order to have a unique solution for the coefficients, a , the matrix [ X + ; y + 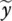] must have n linearly independent columns. However, this matrix has n + 1 columns in total and therefore is rank is deficient by 1. We then must find the smallest matrix [ 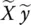] that changes matrix [ X y ] with a rank of n + 1, to a matrix {[ X y ] + [ 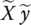]} with a rank n . According to the Eckart‐Young‐Mirsky theorem we can achieve this by defining {[ X y ] + [ 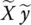]} as the best rank‐ n approximation to [ X y ] and by eliminating the last singular value of [ X y ] which contains the least amount of system information and provides a unique solution. The Eckart–Young–Mirsky theorem ( https://en.wikipedia.org/wiki/Low‐rank_approximation) states a low‐rank approximation is a minimizationproblem, in which the cost functionmeasures the fit between a given matrix (the data) and an approximating matrix (the optimization variable), subject to a constraint that the approximating matrix has reduced rank. To illustrate how this is accomplished, we take the SVD of [ X y ] as follows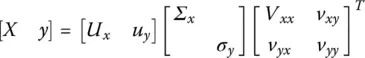

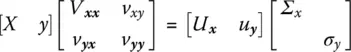
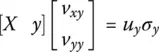
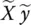(1.32)

where U xhas n columns, u yis a column vector, ∑ xcontains the n largest singular values diagonally, σ yis the smallest singular value, V xxis a n × n matrix, and v yyis scalar. Let us multiple both sides by matrix V .

(1.33)

Next, we will equate just the last columns of the matrix multiplication occurring in (1.32).

(1.34)

From the Eckart‐Young theorem, we know that {[ X y ] + [ ]} is the closest rank‐ n approximation to [ X y ]. Matrix {[ X y ] + [ 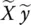]} has the same singular vectors contained in ∑ xabove with σ yequal to zero. We can then write the SVD of {[ X y ] + [ 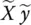]} as such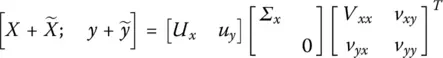

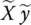(1.35)

To obtain [ ] we must solve the following

(1.36)

(1.36)can be solved by first using (1.32)and (1.35)which results in

(1.37)

Then, from (1.34)we can rewrite (1.37)as

(1.38)