Magdalena Salazar-Palma - Modern Characterization of Electromagnetic Systems and its Associated Metrology

(1.16)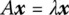

[ A] is assumed to be a square matrix, xis the eigenvector, and λ is a value called the eigenvalue. Normally when any vector xis multiplied by any matrix [ A] a new vector results with components pointing in different directions than the original x. However, eigenvectors are special vectors that come out in the same direction even after they are multiplied by the matrix [ A]. From (1.16)we can see that when one multiplies an eigenvector by [ A], the new vector Ax is just the eigenvalue λ times the original x. This eigenvalue determines whether the vector xis shrunk, stretched, reversed, or unchanged. Eigenvectors and eigenvalues play crucial roles in linear algebra ranging from simplifying matrix algebra such as taking the 500 thpower of [ A] to solving differential equations. To take the 500 thpower of [ A], one only needs to find the eigenvalues and eigenvectors of [ A] and take the 500 thpower of the eigenvalues. The eigenvectors will not change direction and the multiplication of the 500 thpower of the eigenvalues and the eigenvectors will result in [ A] 500. As we will see in later sections, the eigenvalues can also provide important parameters of a system transfer function such as the poles.

One way to characterize and extract the eigenvalues of a matrix [ A] is to diagonalize it. Diagonalizing a matrix not only provides a quick way to extract eigenvalues but important parameters such as the rank and dimension of a matrix can be found easily once a matrix is diagonalized. To diagonalize matrix [ A], the eigenvalues of [ A] must first be placed in a diagonal matrix, [ Λ]. This is completed by forming an eigenvector matrix [ S] with the eigenvectors of [ A] put into the columns of [ S] and multiplying as such

(1.17)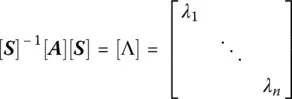

(1.17)can now be rearranged and [ A] can also be written as

(1.18)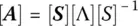

We start to encounter problems when matrices are not only square but also rectangular. Previously we assumed that [ A] was an n by n square matrix. Now we will assume [ A] is any m by n rectangular matrix. We would still like to simplify the matrix or “diagonalize” it but using [ S] ─1[ A][ S] is no longer ideal for a few reasons; the eigenvectors of [ S] are not always orthogonal, there are sometimes not enough eigenvectors, and using A x = λ x requires [ A] to be a square matrix. However, this problem can be solved with the singular value decomposition but of course at a cost. The SVD of [ A] results in the following

(1.19)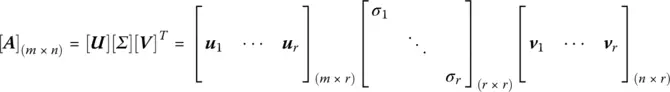

where m is the number of rows of [ A], n is the number of columns of [ A], and r is the rank of [ A]. The SVD of [ A], which can now be rectangular or square, will have two sets of singular vectors, u’s and v’s. The u’s are the eigenvectors of [ A][ A]* and the v’s are the eigenvectors of [ A] T[ A]. [ U] and [ V] are also unitary matrices which means that [ U]*[ U] =[ I] and [ V]*[ V] = [ I]. In other words, they are orthogonal where * denoted complex conjugate transpose. The σ ’s are the singular values which also so happen to be the square roots of the eigenvalues of both [ A][ A] *and [ A] *[ A]. We are not totally finished however because [ U] and [ V] are not square matrices. While (1.19)is the diagonalization of [ A], the matrix equation is technically not valid since we cannot multiply these rectangular matrices of different sizes. To make them square we will need n – r more v’s and m – r more u’s. We can get these required u’s and v’s from the nullspace N( A) and the left nullspace N( A*). Once the new u’s and v’s are added, the matrices are square and [ A] will still equal [ U][ ∑][ V] T. The true SVD of [ A] will now be

(1.20)

The new singular value matrix [∑] is the same matrix as the old r × r matrix but with m – r new rows of zero and n – r columns of new zero added. The theory of total least squares (TLS) heavily utilizes the SVD as will be seen in the next section.

As an example consider the letter X. We now discretize the image on a 20×20 grid as seen in Figure 1.1. We place a 1 where there is no portion of the letter Xand a zero where there is some portion of the letter. This results in the following matrix (1.21)representing the letter Xdigitally on a 20×20 grid of the matrix A. Now if we ask the question “What is the information content in the matrix Xconsisting of 1’s and 0’s ?Clearly one would not require 20×20 = 400 pieces of information to represent Xin (1.21)as there is a lot of redundancy in the system. This is where the SVD comes in and addresses this issue in quite a satisfactory way. If one performs a SVD of the matrix A given by (1.21), one will find that diagonal ∑ matrix in (1.20)has a lot of zero entries. In fact only seven of the singular values are not close to zero as presented in Table 1.1. This implies that the information content of the picture in Figure 1.1is small. The SVD can also be used to reconstruct the original data matrix with reduced information without sacrificing any accuracy.

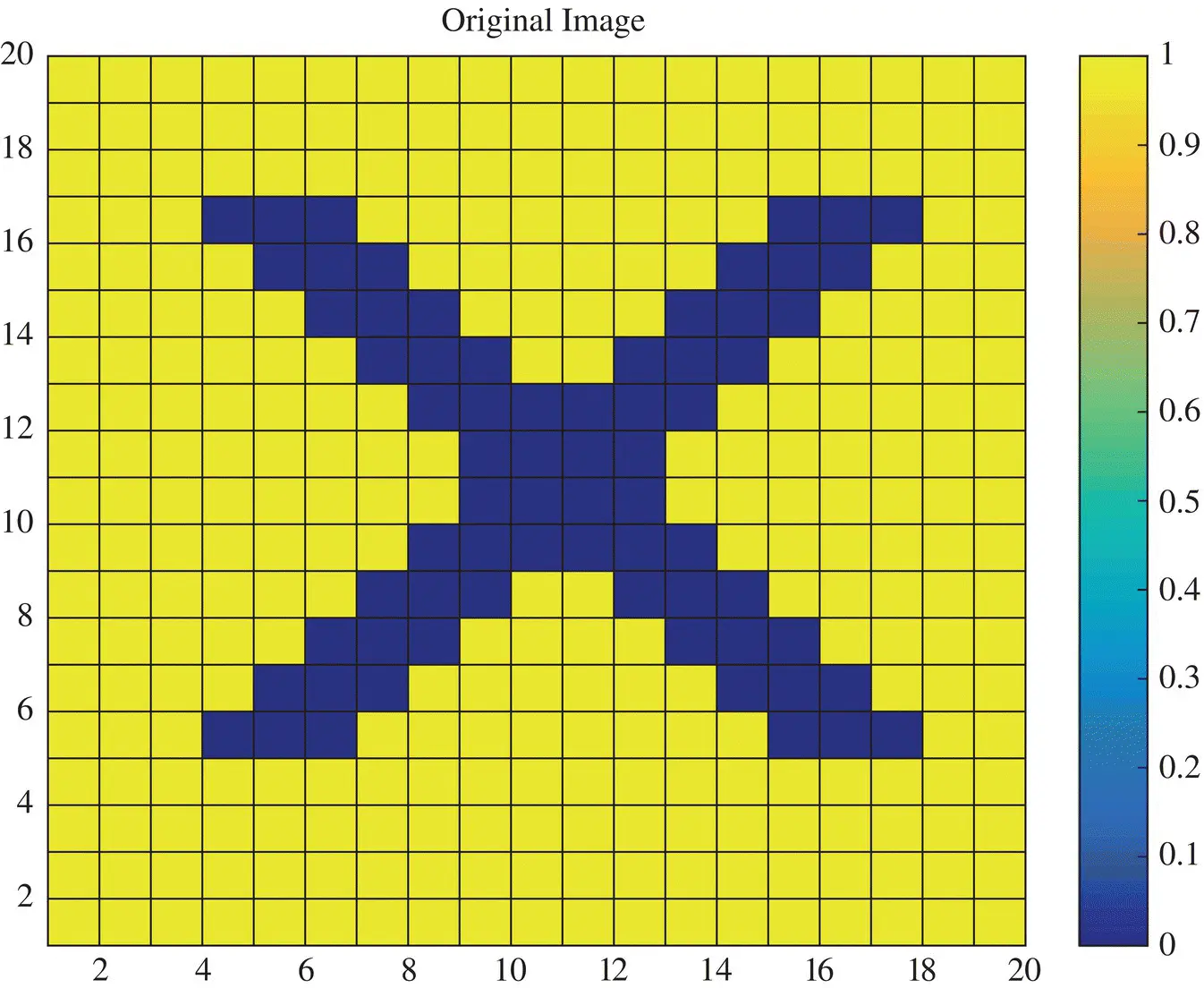
Figure 1.1 Discretization of the letter X on a 20×20 grid.

Table 1.1 List of all the singular values of the matrix A.

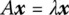
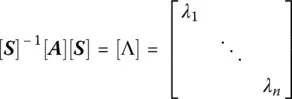
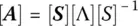
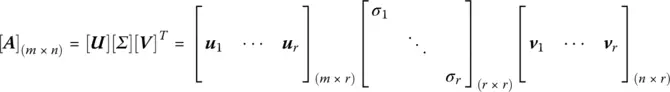
(1.21) (1.21)