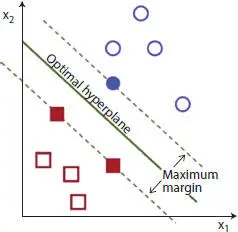
Figure 1.5 Hyperplane in SVM.
Although SVMs look more computationally intensive, this model can be used to predict classes once data training is completed, even when we come across new unlabelled data. In KNN, however, each time we come across a collection of new unlabelled data, the distance metric is determined. In KNN, therefore, we still need to specify the distance metric. There are two major cases of SVMs in which groups can be linearly or non-linearly separable. We use kernel functions such as the Gaussian basis function or polynomials when the classes are non-linearly separable [11].
Therefore, we only have to set the K parameter and select the distance metric appropriate for KNN classification, while in SVMs, if the classes are not linearly separable, we only have to select the R parameter (regularisation term) and also the kernel parameters. Table 1.1gives the comparison between 2 classifiers to check accuracy.
When we check about accuracy of both of the classifiers, SVMs usually have higher accuracy than KNN as shown [6–8].
When performing the visual studio tests after integrating OpenCV libraries, the accuracy percentage for SVM [7] was found to be 94 percent and 93 percent for KNN [6].
Table 1.1 Accuracy of classifiers.
| Classifier |
Training set |
Test set |
Accuracy rate (in %) |
| SVM |
10,000 |
10,000 |
98.9 |
| KNN |
10,000 |
10,000 |
96.47 |
1.3 Mathematical Models and Covid-19
The compartmental models are divided into different groups depending on the essence of the disease and its pattern of spread:
1 Susceptible-Infected-Recovered (SIR): This model divides the N-size population into three epidemiological overview subpopulations; Susceptible, Contaminated and Recovered, represented respectively by variables S, I and R. It is also possible to add birth, mortality and vaccination rates to this model. Individuals in the susceptible class are born. Infected individuals transmit the disease to susceptible individuals and stay in the infected class (the infected period) and individuals are believed to be resistant to life in the recovered class.
2 Susceptible-Exposed-Infected-Recovered (SEIR): This model divides the N-size population into four epidemiological overview subpopulations; Prone, Exposed, Contaminated, and Recovered, represented respectively by variables S, E, I, and R. In this model, birth rate, death rate, and vaccination rate, if known/applicable, can also be considered. For a disease where there is a substantial post-infection incubation period in which an infected person is not yet infectious, this is an acceptable model.
3 Susceptible-Infected-Susceptible (SIS): Some diseases, such as those caused by the common cold, do not have long-lasting immunity. Upon recovery from infection, certain infections do not have immunisation and individuals become susceptible again.
4 Susceptible-Exposed-Infected-Susceptible (SEIS): When there is no immunity to the pathogen, this model can be used (implying that the R class would be zero). Tuberculosis can be an instance of this model [12].
1.3.1 SEIR Model (Susceptible-Exposed-Infectious-Removed)
To estimate the infected numbers, the traditional Susceptible-Exposed-Infected-Recovered (SEIR) model is used. Viruses or bacteria are the cause of infectious diseases such as rubella, mumps, measles and pertussis. The transmission of these diseases requires a time of incubation. The incubation period is a period in which clinical signs are displayed by people who have started being attacked by viruses or bacteria but have not been able to spread the disease. The Susceptible-Exposed-Infected-Recovery (SEIR) model can reflect the spread of illness by observing the incubation time. Immigration has an effect on the spread of illness. This is caused by refugees who may bring the disease from their regions to other countries. For this reason, the immigration SEIR model should be considered. We will define the SEIR model with immigration here, decide an equilibrium point and state the stability of the equilibrium. The model is then extended to the illness of herpes [13].
In analysing the spread and control of infectious diseases, mathematical models have become valuable tools. Most research on outbreak models also involves the disease’s persistence and extinction. In mathematical epidemiology, the majority of models are compartments. For diseases with a longer incubation period, a population is divided into prone, exposed, infectious, and recovered compartments in some traditional research studies; the model is then called the SEIR model. Figure 1.6shows data representation at different point of contact.
Figure 1.7is about SIR model. The model consists of three comparments:
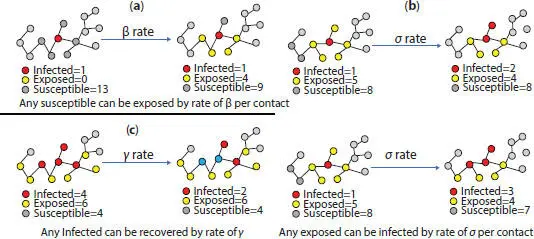
Figure 1.6 Exposed, infection and recovery transmission in SEIR model. (a) Any susceptible can be exposed by rate of per contact point. (b) Infection occurs at rate per contact and (c) recovery occurs at rate for infected population.
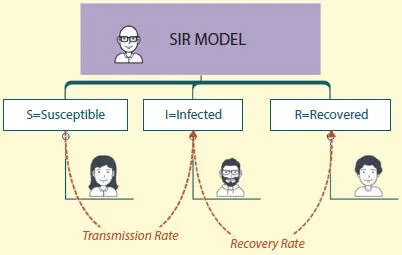
Figure 1.7 SIR model.
S: The number of susceptible individuals. When a susceptible and an infectious individual come into “infectious contact”, the susceptible individual contracts the disease and transitions to the infectious compartment.
I: The number of infectious individuals. These are individuals who have been infected and are capable of infecting susceptible individuals.
R: The number of removed (and immune) or deceased individuals. These are individuals who have been infected and have either recovered from the disease and entered the removed compartment, or died. It is assumed that the number of deaths is negligible with respect to the total population. This compartment may also be called “recovered” or “resistant”.
1.3.2 SIR Model (Susceptible-Infected-Recovered)
The outbreak prediction has become highly complicated for emerging scientific science due to the pandemic scenario of COVID-19 disease cases around the world. To accurately forecast the forecasts, many epidemiological mathematical models of spread are growing daily. In this analysis, to analysis the various parameters of this model for India, the classical susceptible-infected-recovered (SIR) modelling method was used. By considering various governmental lockdown initiatives in India, this method was studied [14].
Estimation of parameters of SIR model of India using an actual data set:
Fundamental models based on compartments, as seen in the following, were used for the epidemic mathematical model:
1 (Susceptible->Infectible) SI model,
2 (Susceptible->Infectible-> Susceptible) SIS model, and
3 (Susceptible->Infectible-> Recovery/Removed) SIR model.
The standard SIR model is basically a series of differential equations that can be classified as susceptible (if previously unexposed to pandemic disease), infected (if presently conquered by pandemic disease), and removed (either by death or recovery) [15].
The goal of this chapter was to present some of the machine learning and AI principles and methodologies and explore some of their possible applications in different aspects of computational mechanics. The methodologies outlined herein are maturing rapidly, and many new applications are likely to be found in computational mechanics. Undoubtedly, AI methodologies would inevitably become, to the same degree as today’s “traditional” algorithmic devices, a natural and indispensable part of the set of computer-based engineering resources. These instruments would then greatly elevate the role of computers in engineering from the current focus on calculation to the much wider field of reasoning.
Читать дальше















