Generalized Ordinary Differential Equations in Abstract Spaces and Applications
Здесь есть возможность читать онлайн «Generalized Ordinary Differential Equations in Abstract Spaces and Applications» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Generalized Ordinary Differential Equations in Abstract Spaces and Applications
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:4 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Generalized Ordinary Differential Equations in Abstract Spaces and Applications: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Generalized Ordinary Differential Equations in Abstract Spaces and Applications»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
Explore a unified view of differential equations through the use of the generalized ODE from leading academics in mathematics Generalized Ordinary Differential Equations in Abstract Spaces and Applications
Generalized Ordinary Differential Equations in Abstract Spaces and Applications
Generalized Ordinary Differential Equations in Abstract Spaces and Applications — читать онлайн ознакомительный отрывок
Ниже представлен текст книги, разбитый по страницам. Система сохранения места последней прочитанной страницы, позволяет с удобством читать онлайн бесплатно книгу «Generalized Ordinary Differential Equations in Abstract Spaces and Applications», без необходимости каждый раз заново искать на чём Вы остановились. Поставьте закладку, и сможете в любой момент перейти на страницу, на которой закончили чтение.
Интервал:
Закладка:
Then, 
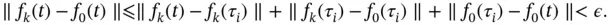
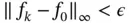and, therefore, 
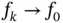uniformly on 
.
Lemma 1.14: Let be a sequence in . The following assertions hold:
1 if the sequence of functions converges uniformly to as on , then , for , and , for ;
2 if the sequence of functions converges pointwisely to as on and , for , and , for , where , then the sequence converges uniformly to as .
Proof. We start by proving 
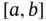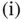. By hypothesis, the sequence 
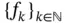converges uniformly to 
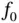. Then, Moore–Osgood theorem (see, e.g., [19]) implies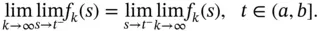
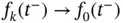Therefore, 
, for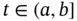 
. In a similar way, one can show that 
, for every 
.
Now, we prove 
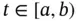. It suffices to show that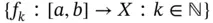 
is an equiregulated set. Indeed, by Lemma 1.13, 
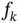converges uniformly to 
.
Since the function 
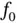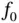is regulated, its lateral limits exist. Then, for every 
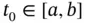and every 
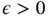, there is 
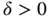such that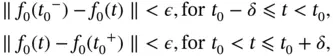
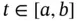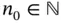for every 
.
But the hypotheses say that we can find 
such that, for 
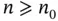, we have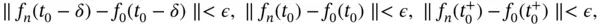
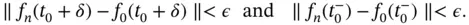
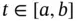When 
satisfies 
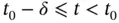, we have, for every 
,
On the other hand, when 
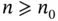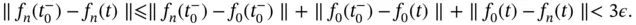
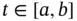satisfies 
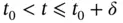, we get, for 
,
But this yields the fact that 
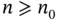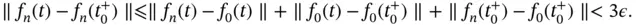
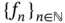is an equiregulated sequence, and the proof is complete.
The next lemma guarantees that, if a sequence of functions 
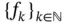is bounded by an equiregulated sequence of functions, then 
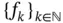is also equiregulated.
Интервал:
Закладка:
Похожие книги на «Generalized Ordinary Differential Equations in Abstract Spaces and Applications»
Представляем Вашему вниманию похожие книги на «Generalized Ordinary Differential Equations in Abstract Spaces and Applications» списком для выбора. Мы отобрали схожую по названию и смыслу литературу в надежде предоставить читателям больше вариантов отыскать новые, интересные, ещё непрочитанные произведения.
Обсуждение, отзывы о книге «Generalized Ordinary Differential Equations in Abstract Spaces and Applications» и просто собственные мнения читателей. Оставьте ваши комментарии, напишите, что Вы думаете о произведении, его смысле или главных героях. Укажите что конкретно понравилось, а что нет, и почему Вы так считаете.