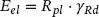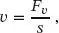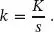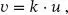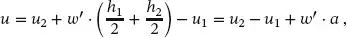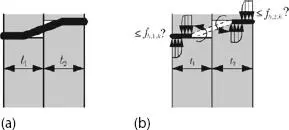
Abb. 1.8 Einschnittige Holz-Holz-Verbindung (a) Versagensmechanismus mit zwei Fließgelenken (b) Lochleibungsspannungen.
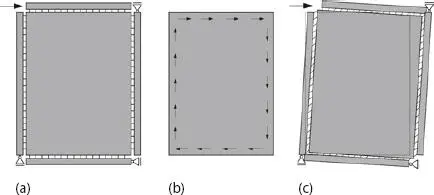
Abb. 1.9 Schubfeldmodell: (a) statisches System, (b) Annahme Schubfluss und (c) Verformungen.
1.3.4 Kapazitätsbemessung
Die Übertragung von Rechenmodellen, welche auf der Grundlage der Plastizitätstheorie hergeleitet wurden, auf reale Tragwerke erfolgt im Rahmen einer Kapazitätsbemessung. Das Ziel dieser Bemessung ist es sicherzustellen, dass der in der Theorie vorausgesetzte plastische Mechanismus erreicht wird und das Tragwerk nicht an anderer Stelle vorzeitig versagt. Bei der Bemessung von Anschlüssen mit stiftförmigen Verbindungen werden in diesem Zusammenhang Mindestabstände für die einzelnen Verbindungsmittel definiert, um ein sprödes Versagen des Holzes im Anschlussbereich auszuschließen. Bei Wandtafeln gibt es mehrere am Lastabtrag beteiligte Tragelemente, deren Versagen durch die Kapazitätsbemessung ausgeschlossen werden soll. Dazu zählen die knickgefährdete Randrippe, die Holzwerkstoffplatte als Schubfeld und die Zugverankerung. Für diese Tragelemente wird im Rahmen der Kapazitätsbemessung eine erhöhte Einwirkung E elangesetzt, die sich aus dem charakteristischen Wert des Tragwiderstandes des plastisch verformten Tragelementes Rpl und einem Überfestigkeitswert γ Rdzusammensetzt.
(1.38) 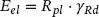
Konkrete Regelungen zur Überfestigkeit finden sich in Abschn. 4.3mit Bezug zur Auslegung von Tragwerken gegenüber Erdbebeneinwirkungen.
1.4 Berechnungsverfahren für zusammengesetzte Querschnitte – γ -Verfahren
Die Wirkungsweise von zusammengesetzten Querschnitten wird in Abb. 1.10für unterschiedliche Verbindungen der beiden Teilquerschnitte veranschaulicht; von der Tragwirkung der Einzelquerschnitte über den nachgiebigen zum starren Verbund. Es ist zu erkennen, dass das Ebenbleiben des Gesamtquerschnitts nur bei Bauteilen mit starrem Verbund gewährleistet ist. Bei Querschnitten mit nachgiebigem Verbund gilt die Bernoulli-Hypothese nicht, welche das Ebenbleiben der Querschnitte voraussetzt, und somit sind die Regeln der technischen Biegelehre auf diese Querschnitte nicht direkt anwendbar. Die Biegesteifigkeit von aufeinander gelegten Balken entspricht der Summe der Biegesteifigkeiten der Einzelquerschnitte, solange in der Kontaktfuge keine Schubkräfte übertragen werden.
Die Schnittgrößen nachgiebig miteinander verbundener Querschnitte können mit dem γ -Verfahren ermittelt werden. Dieses für die Handrechnung geeignete Verfahren wurde von Fritz Stüssi (1943) und Karl Möhler (1956) entwickelt. Es wurde für Einfeldträger mit gleichmäßigem Schubfluss und einer sinusförmigen Belastung hergeleitet, liefert aber auch für Einfeldträger unter Gleichstreckenlast eine ausreichend genaue Näherung. Von einem gleichmäßigen Schubfluss kann ausgegangen werden, wenn die Verbindungsmittel in einem vergleichsweise geringen Abstand angeordnet werden.
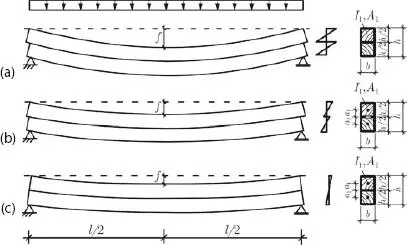
Abb. 1.10 Zusammenwirken von Querschnitten: (a) zwei Einzelquerschnitte ohne Verbund, (b) nachgiebiger Verbund und (c) starrer Verbund.
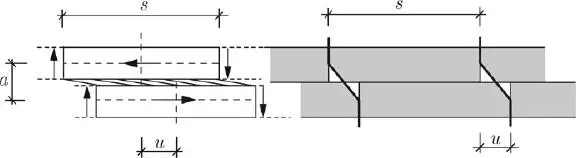
Abb. 1.11 Definition von Kräften und Verschiebungen im Bereich der Verbundfuge.
Vereinfacht werden die im Abstand s angeordneten Verbindungsmittel zu einer kontinuierlichen Schubübertragung und der zugehörigen Steifigkeit der Verbundfuge umgerechnet (siehe Abb. 1.11):
(1.39) 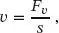
(1.40) 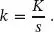
Der Zusammenhang zwischen der Relativverschiebung u der Querschnittsteile und der zugehörigen Kraft wird dann mit folgender Gleichung beschrieben:
(1.41) 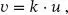
mit
| F ν |
Scherkraft pro Verbindungsmittel, |
| s |
Abstand der Verbindungsmittel, |
| ν |
Schubkraft pro Längeneinheit, |
| K |
Steifigkeit pro Verbindungsmittel bei Scherbeanspruchung, |
| k |
Steifigkeit der Verbundfuge pro Längeneinheit, |
| u |
Relativverschiebung der Querschnitte in der Verbundfuge. |
Diese Angaben beziehen sich auf eine einreihige Anordnung der Verbindungsmittel. Werden mehrere Verbindungsmittel nebeneinander angeordnet, dann erhöht sich die Steifigkeit entsprechend.
Im Folgenden sollen anhand der Gleichgewichtsbedingungen für die Schnittgrößen mit den zugehörigen Spannungs-Dehnungs-Beziehungen die Differenzialgleichungen für einen aus zwei Teilen bestehenden zusammengesetzten Querschnitt aufgestellt werden. Dabei wird angenommen, dass für jeden Teilquerschnitt die Bernoulli-Hypothese gilt. Die Abmessungen der einzelnen Querschnitte sind über die Länge der Stabachse konstant.
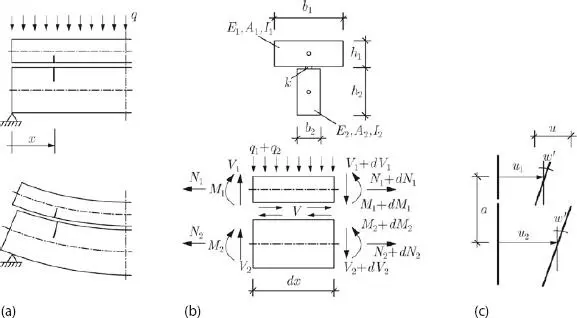
Abb. 1.12 Verbundträger: (a) Seitenansicht im Auflagerbereich, (b) geometrische Größen und Schnittgrößen und (c) Definition der Relativverschiebung.
Die Relativverschiebung u der Querschnittsteile in der Höhe der Verbundfuge, wie sie in Abb. 1.12definiert ist, ergibt sich zu
(1.42) 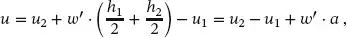
mit
| u 1, u 2 |
Längsverschiebungen der Querschnitte 1 und 2, |
| w |
Durchbiegung des Verbundträgers und der Teilquerschnitte, |
| s |
Abstand der Schwerpunkte der Teilquerschnitte, |
| h 1, h 2, b 1, b 2 |
Abmessungen der Teilquerschnitte, |
| A 1, A 2, I 1, I 2 |
Querschnittsfiächen und Flächenträgheitsmoment der Teilquerschnitte, |
| E 1, E 2 |
Elastizitätsmodul der Teilquerschnitte. |
Die Relativverschiebung u der einzelnen Querschnitte ist unabhängig von der Lage der Verbundfuge und wird nur durch den Abstand a der Schwerachsen der beiden Querschnitte beEinflusst. Die Schnittgrößen lassen sich auf Grundlage der Elastizitätsgesetze nach der Balkentheorie bestimmen.
Читать дальше