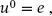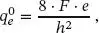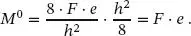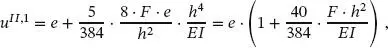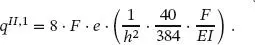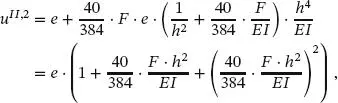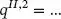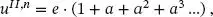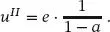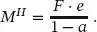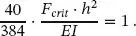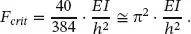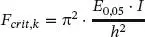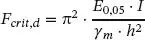Werner Seim - Ingenieurholzbau

Zum Einstieg in die Berechnung von Schnittgrößen am verformten System muss eine Vorverformung definiert werden. Ohne Vorverformung sind die Schnittgrößen nach Theorie I. und II. Ordnung identisch. Reale Tragelemente sind normalerweise nicht perfekt und weisen deshalb – herstellungs- oder auch transportbedingt – Abweichungen von den vorgegebenen Systemlinien auf. Diese Abweichungen werden als Imperfektionen bezeichnet und sind in den Konstruktionsnormen festgelegt (siehe Abb. 1.20). Diese Imperfektionen könnten beim geometrischen Modell des Tragwerks direkt durch gekrümmte und schräg stehende Stäbe berücksichtigt werden. Einfacher und vom Ergebnis her gleichwertig ist es, wenn anstelle der Imperfektionen Ersatzkräfte in die Berechnung eingeführt werden. Abbildung 1.19zeigt dieses Vorgehen am Beispiel eines beidseitig gelenkig gelagerten Druckstabs und schematisch für den kippgefährdeten Einfeldträger.

Mit der Vorgabe der Imperfektion bzw. der entsprechenden Ersatzlast liegt der Startwert für die iterative Berechnung der Schnittgrößen nach Theorie II. Ordnung fest. Für einfache System können die Schnittgrößen nach Theorie II. Ordnung ohne Weiteres von Hand ermittelt werden. Für den beidseitig gelenkig gelagerten Druckstab aus Abb. 1.19lassen sich die Durchbiegungen schrittweise berechnen, indem der Verformung in Stabmitte immer wieder der zusätzliche Anteil aus dem Biegemoment des vorhergehenden Iterationsschrittes zugeschlagen wird.

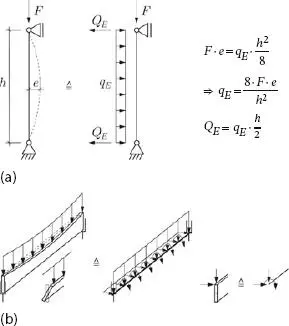
Abb. 1.19 Ersatzkräfte für Imperfektionen: (a) Druckstab und (b) kippgefährdeter Träger.

Ausgangswerte

(1.84)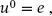

(1.85)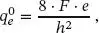

(1.86)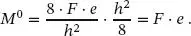

1. Iteration

(1.87)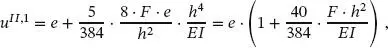

(1.88)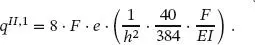

2. Iteration

(1.89)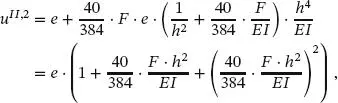

(1.90)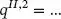

n. Iteration

(1.91)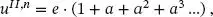

mit

Für n →∞ ist dies eine geometrische Reihe und die Verformung in Stabmitte nach Theorie II. Ordnung liegt fest mit

(1.92)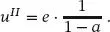

Das zugehörige Biegemoment beträgt

(1.93)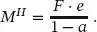

Die kritische Last Fcrit wird erreicht, wenn M → ∞. Das ist der Fall, wenn a → 1:

(1.94)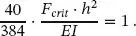

Die kritische Last, also die Knicklast, lässt sich somit angeben zu:

(1.95)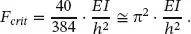

Der Unterschied zur genauen Knicklast nach Euler beträgt weniger als 3 % und ist darauf zurückzuführen, dass anstelle einer sinusförmigen eine parabelförmige Verformungsfigur angenommen wurde.

Für die praktische Anwendung der Berechnungsverfahren nach Theorie II. Ordnung sind konkrete Werte für Imperfektionen in Abb. 1.20angegeben. Bei Systemen mit mehreren Stäben sind Imperfektionen – in Analogie zu den äußeren Einwirkungen – immer in die Richtung anzusetzen, in der sie die Schnittgrößen vergrößern. Daraus kann schnell eine große Anzahl unübersichtlicher Imperfektionskombinationen werden, welche von einem kommerziellen Rechenprogramm zuverlässig beherrscht werden sollten.

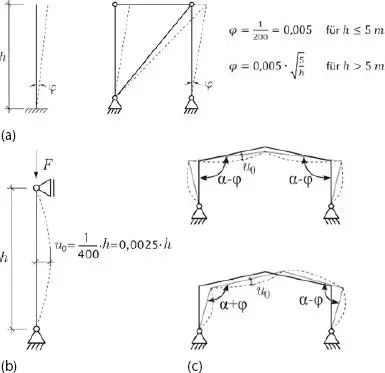
Abb. 1.20 Imperfektionen: (a) Schiefstellung, (b) Vorkrümmung und (c) Überlagerung von Schiefstellung und Vorkrümmung.

Tab. 1.1.Verformungsmoduln für die Schnittgrößenermittlung nach Theorie II. Ordnung.

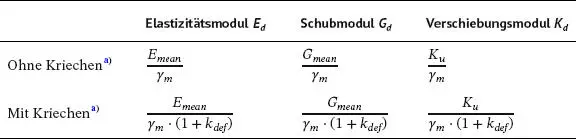
a) Zu berücksichtigen ist der KriechEinfluss bei druckbeanspruchten Bauteilen in der Nutzungsklasse 2 und wenn der Bemessungswert des quasiständigen Lastanteils größer als 70 % des Bemessungswertes der Gesamtlast ist.

Der Übergang von charakteristischen Werten zu Bemessungswerten der Tragfähigkeit könnte bei großen Schlankheiten umgesetzt werden, indem ein charakteristischer Wert der Knicklast

(1.96)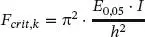

mit dem gewohnten Teilsicherheitsbeiwert γ mzu einem Bemessungswert des Tragwiderstandes

(1.97)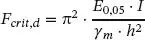

wird.

Die Auswirkung von Kriechverformung auf die Schnittgrößen könnten berücksichtigt werden, indem man – wie bei der Verformungsberechnung – die Steifigkeit für den entsprechenden Lastanteil mit kdef abmindert.

Tabelle 1.1 fasst die aktuellen normativen Regelungen zusammen. Bei den Steifigkeiten dürfen demnach die durch γ mabgeminderten Mittelwerte angesetzt werden, bei Verbindungen die mit γ mabgeminderten Verschiebungsmoduln K u .

Für den Spannungsnachweis kann die im Band 1, Abschn. 2.5.4 vorgestellte Interaktionsbedingung mit quadratischem Normalspannungsanteil verwendet werden.

Blaß, H.J., Ehlbeck, J., Kreuzinger, H. und Steck, G. (2005). Erläuterungen zu DIN 1052: 2004–2008 , 2. Aufi. DGfH, München/Karlsruhe: Bruderverlag.

Colling, F. (1990). Tragfähigkeit von Biegeträgern aus Brettschichtholz in Abhängigkeit von den festigkeitsrelevanten Einflussgrößen. Dissertation, TH Karlsruhe.

Foschi, R.O. und Barrett, J.D. (1980). Gluedlaminated beam strength: A model. J. Struct. Div. Am. Soc. Civil Eng . 106 (ST8): 1735–1754.

Gustafsson, P.J. (1988). A study of strength of notched beams. Proceedings of 21st Meeting of CIB-W18, Parksville, Canada, 1988.