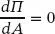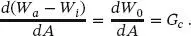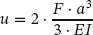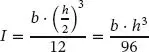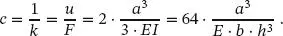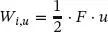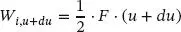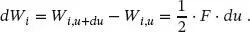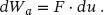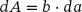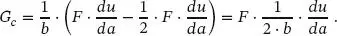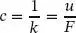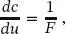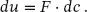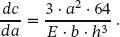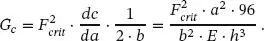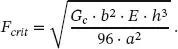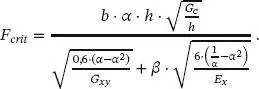Das Risswachstum erreicht den kritischen Wert ac und geht in einen instabilen Bereich über, wenn das Maximum der Gesamtenergie erreicht ist (siehe Abb. 1.6a):
(1.17) 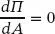
(1.18) 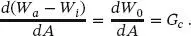
Die in diesem Zusammenhang definierte Griffith-Konstante Gc ist als Verhältnis der freigewordenen Energie zur Änderung der Bruchfläche definiert. Für das Beispiel aus Abb. 1.5können die gespeicherte Energie Wi und die Arbeit der äußeren Lasten Wa mit der Biegesteifigkeit der Einzelquerschnitte ermittelt werden. Die Formänderungsenergie Wi wird über die Verformung der Einzelquerschnitte für u und u + du in Abb. 1.6bdargestellt. Dabei wird vorausgesetzt, dass der Riss bereits instabil ist, d. h., er wächst, ohne dass die Kraft zunimmt. Damit ist die kritische Bruchlast Fcrit erreicht.
Mit
(1.19) 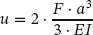
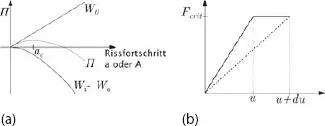
Abb. 1.6 (a) Energiebilanz und (b) Last-Verformungs-Beziehung beim Rissfortschritt.
und
(1.20) 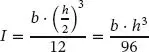
lässt sich eine Ersatzfedersteifigkeit für die beiden Kragarme in Abb. 1.5beschreiben:
(1.21) 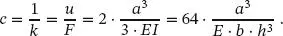
Der Zuwachs der inneren Arbeit (Formänderungsenergie) ergibt sich aus der Differenz von
(1.22) 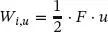
und
(1.23) 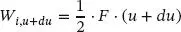
(1.24) 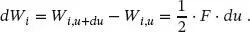
Der Zuwachs der äußeren Arbeit lässt sich angeben als:
(1.25) 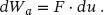
Durch Einsetzen von Gln. ( 1.23) und ( 1.24) in Gl. ( 1.18) folgt mit
(1.26) 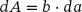
(1.27) 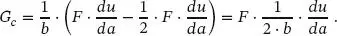
Mit der Definition der Ersatzfedersteifigkeit
(1.28) 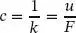
und deren Ableitung nach u
(1.29) 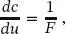
erhält man
(1.30) 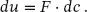
Die Ableitung von Gl. ( 1.21) nach a ergibt
(1.31) 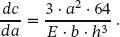
Mit Gln. ( 1.30) und ( 1.31) in Gl. ( 1.27) eingesetzt, lässt sich eine Bezeichnung zwischen der kritischen Bruchlast und der Griffith-Konstanten angeben:
(1.32) 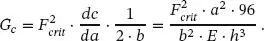
Die zugehörige kritische Bruchlast beträgt:
(1.33) 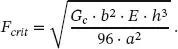
Folgende Bezeichnungen wurden für diese Herleitung verwendet:
| u |
Größe der Verformung zwischen den Kragträgern, |
| b |
Breite der Rissfiäche bzw. des Bauteils, |
| a |
Abstand der Lasteinleitung zum Ende des Einschnitts, |
| F |
aufgebrachte Last, |
| E |
E-Modul des Werkstoffs, |
| I |
Flächenträgheitsmoment des Einzelquerschnitts, |
| k |
Federkennwert des Biegeträgers, |
| c = 1/ k |
Federsteifigkeit, |
| d u |
Änderung der Rissöffnung, |
| d a |
Änderung der Risslänge, |
| d c |
Änderung der Ersatz-Federsteifigkeit, |
| G c |
Bruchenergie [J/m 2] oder [N/mm]. |
Die auf eine infinitesimale Fläche bezogene Energiefreisetzung kann als spezifische Bruchenergie aufgefasst werden. Die Größe der Griffith-Konstanten lässt sich über die Fläche unter dem Last-Verformungs-Diagramm nach Abb. 1.4bveranschaulichen. Hier wurde eine bilinear vereinfachte Spannungs-Dehnungs-Beziehung verwendet, deren Flächeninhalt der spezifischen Bruchenergie entspricht. Die Bruchenergie des Holzes ist maßgeblich von der Rohdichte abhängig und liegt für Nadel- und Brettschichtholz etwa bei G c= 0,3 N/mm 2für Zugbeanspruchung senkrecht zur Faserrichtung. Die Bruchenergie wird aus Versuchen ermittelt.
Die Gleichung für die kritische Kraft Fcrit zeigt, dass die maximal aufzubringende Kraft nicht direkt von der Querzugfestigkeit des Materials abhängig ist. Die bestimmenden Werkstoffparameter sind die spezifische Bruchenergie und der E-Modul. Eine zweite Erkenntnis aus Gl. ( 1.33) ist die starke Abhängigkeit der Bruchlast von der Querschnitthöhe. Dies zeigt, dass ein reiner Spannungs-Festigkeits-Nachweis der Bauteilgeometrie am Riss nicht ausreicht, da sich ein Maßstabseffekt ergibt, der bei der Bemessung zu berücksichtigen ist.
1.2.3 Anwendung der Bruchmechanik
Die im vorgehenden Abschnitt ausführlich beschriebene Vorgehensweise kann nun auf konkrete statisch-konstruktive Randbedingungen angewandt werden. Gustafsson (1988) leitet für das in Abb. 1.7dargestellte Auflager eines symmetrischen Trägers mit der Breite b die kritische Last her:
(1.34) 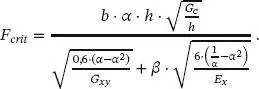
Dabei berücksichtigt er die elastischen Anteile aus der Biege- und Schubverformung des Trägers mit dem Elastizitätsmodul Ex und dem Schubmodul Gxy sowie die zusätzliche elastische Verformung im Bereich der Ausklinkung als Kragarm bis zur Rissspitze. Die Beiwerte α und β beschreiben die Geometrie der Ausklinkung (siehe Band 1, Abschn. 2.8.3).
Читать дальше