Saeid Sanei - EEG Signal Processing and Machine Learning

Lewis electronic membrane models are based on the Hodgkin–Huxley equations. All the components are parallel circuits connected between nodes representing the inside and outside of the membrane. He realized the sodium and potassium conductances using electronic hardware in the form of active filters. Since the model output is the transmembrane voltage V m, the potassium current can be evaluated by multiplying the voltage corresponding to G Kby ( V m− V K). Figure 3.14is consequently an accurate physical analogue to the Hodgkin–Huxley expressions, and the behaviour of the output voltage V mcorresponds to that predicted by the Hodgkin–Huxley equations. The electronic circuits in the Lewis neuromime had provision for inserting (and varying) not only such constants as G K max, G Na max, V K, V Na, V Cl, which enter the Hodgkin–Huxley formulation, but also τ h , τ m , τ n, which allow modifications from the Hodgkin–Huxley equations. In this realization the voltages of the biological membrane are multiplied by 100 to fit the electronic circuit. In other quantities, the original values of the biological membrane have been used.

As in Figure 3.15, Roy also introduced a model based on the Hodgkin–Huxley model [58]. He used field‐effect transistors (FETs) to simulate the sodium and potassium conductances in the membrane model [58].

In the Roy model the conductance is controlled by a circuit including an operational amplifier, capacitors, and resistors. This circuit is designed to make the conductance behave according to the Hodgkin–Huxley model. Roy's main goal was to achieve a very simple model rather than to simulate accurately the Hodgkin–Huxley model.

The Lewis model is based on the Hodgkin–Huxley membrane model and the theories of Eccles on synaptic transmission [59]. The model circuit is illustrated in Figure 3.16. This neuron model is divided into two sections: the synaptic section and the section generating the action pulse. Both sections consist of parallel circuits connected to the nodes representing the intracellular and extracellular sites of the membrane.

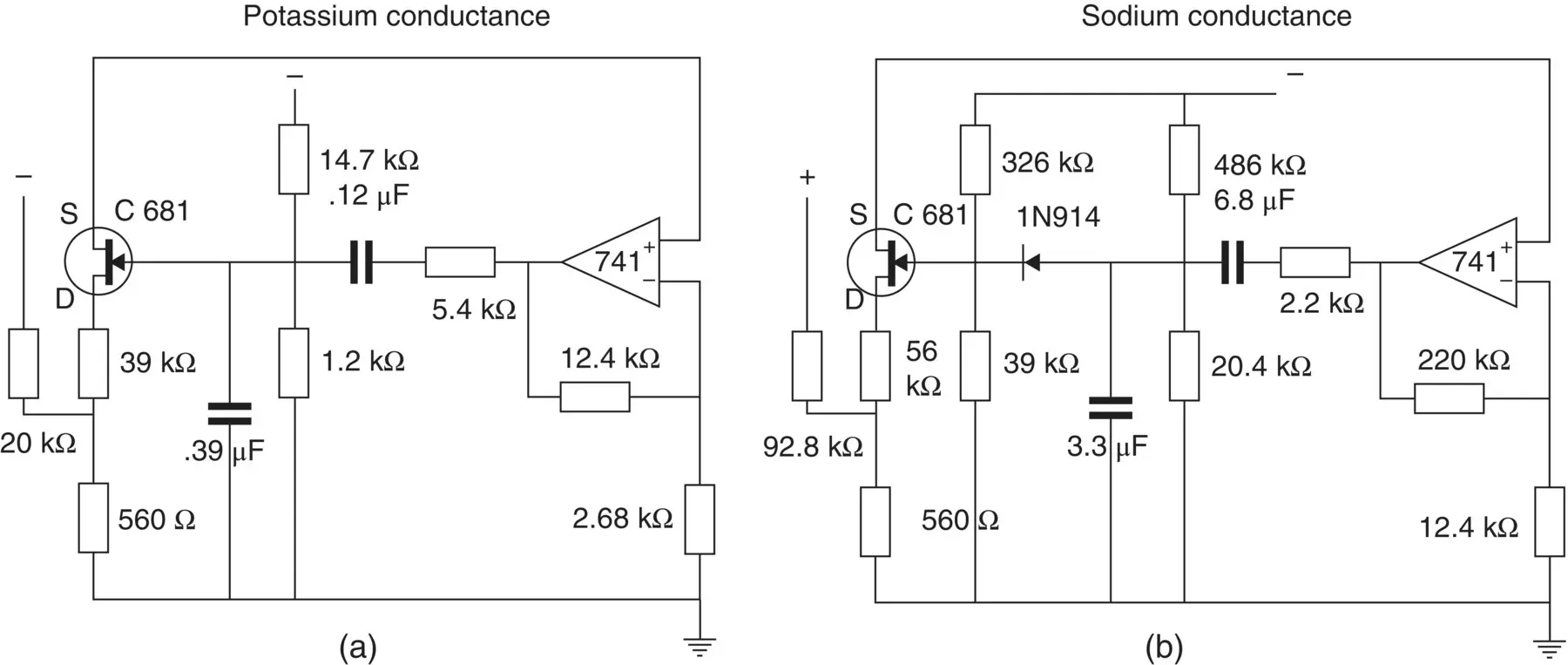
Figure 3.15 Circuits simulating (a) potassium and (b) sodium conductances in the Roy membrane model [58].

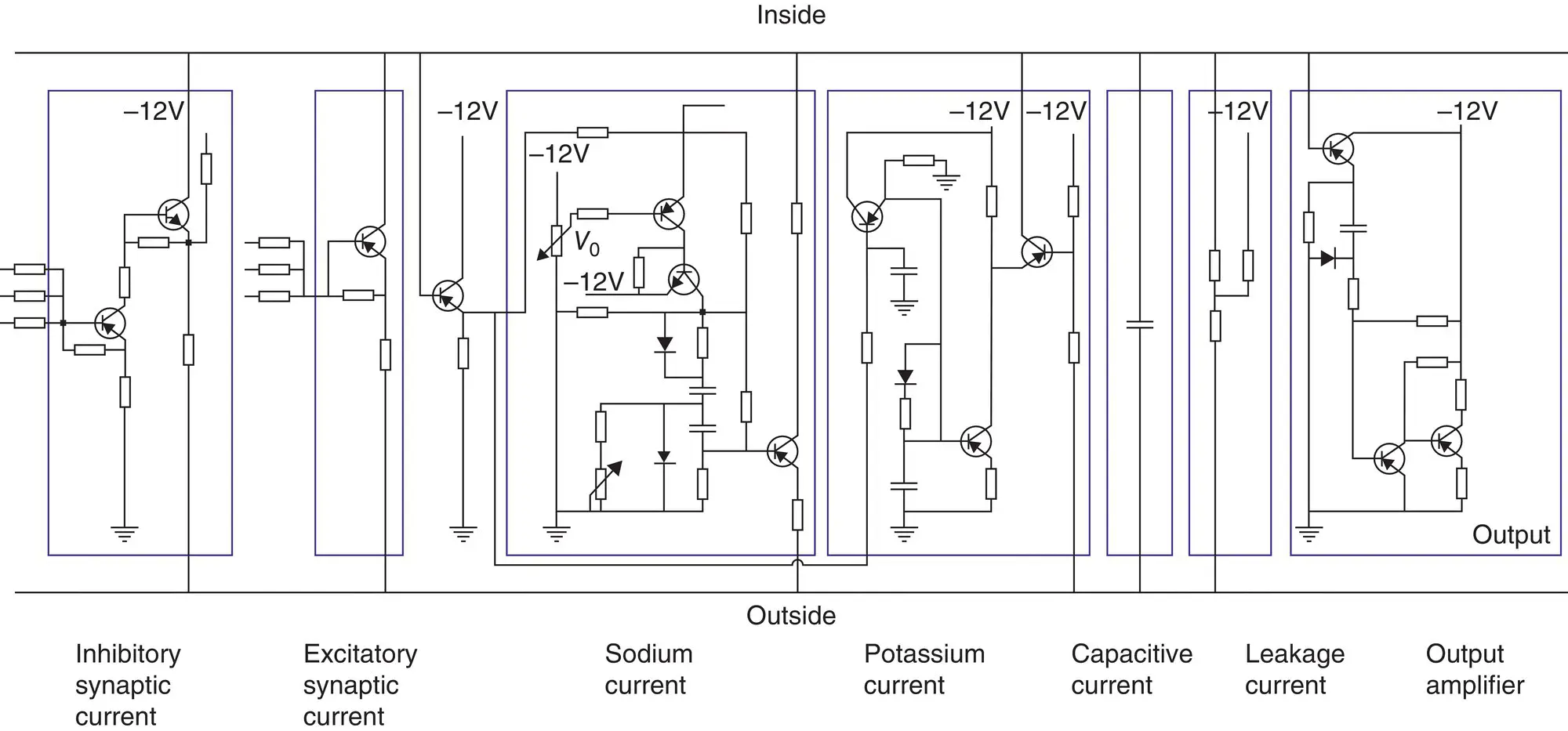
Figure 3.16 The Lewis neuron model from 1968 [57].

The section representing the synaptic junction is divided into two components: the inhibitory junction and the excitatory junction. The sensitivity of the section generating the action pulse to a stimulus introduced at the excitatory synaptic junction is reduced by the voltage introduced at the inhibitory junction. The section generating the action pulse is based on the Hodgkin–Huxley model which consists of the normal circuits simulating the sodium and potassium conductances, the leakage conductance, and the membrane capacitance. The circuit also includes an amplifier for the output signal. This model may be used in research on neural networks. However, it is actually a simplified version of Lewis's 46‐transistor network having the same form. The purpose of this simplified Lewis model is to simulate the form of the action pulse with moderate accuracy following simple models.

The electronic realizations of the Hodgkin–Huxley model are very accurate in simulating the function of a single neuron. However, these circuits are often very complicated. Leon D. Harmon managed to develop a neuron model having a very simple circuit [60]. A circuit of the Harmon neuron model is given in Figure 3.17. The model is equipped with five excitatory inputs which can be adjusted. These include diode circuits representing various synaptic functions. The signal introduced at excitatory inputs charges the 0.02 μF capacitor which, after reaching a voltage of approximately 1.5 V, allows the monostable multivibrator, formed by transistors T1 and T2, to generate the action pulse. This impulse is amplified by transistors T3 and T4. The output of one neuron model may drive the inputs of a large number of the neighbouring neuron models.

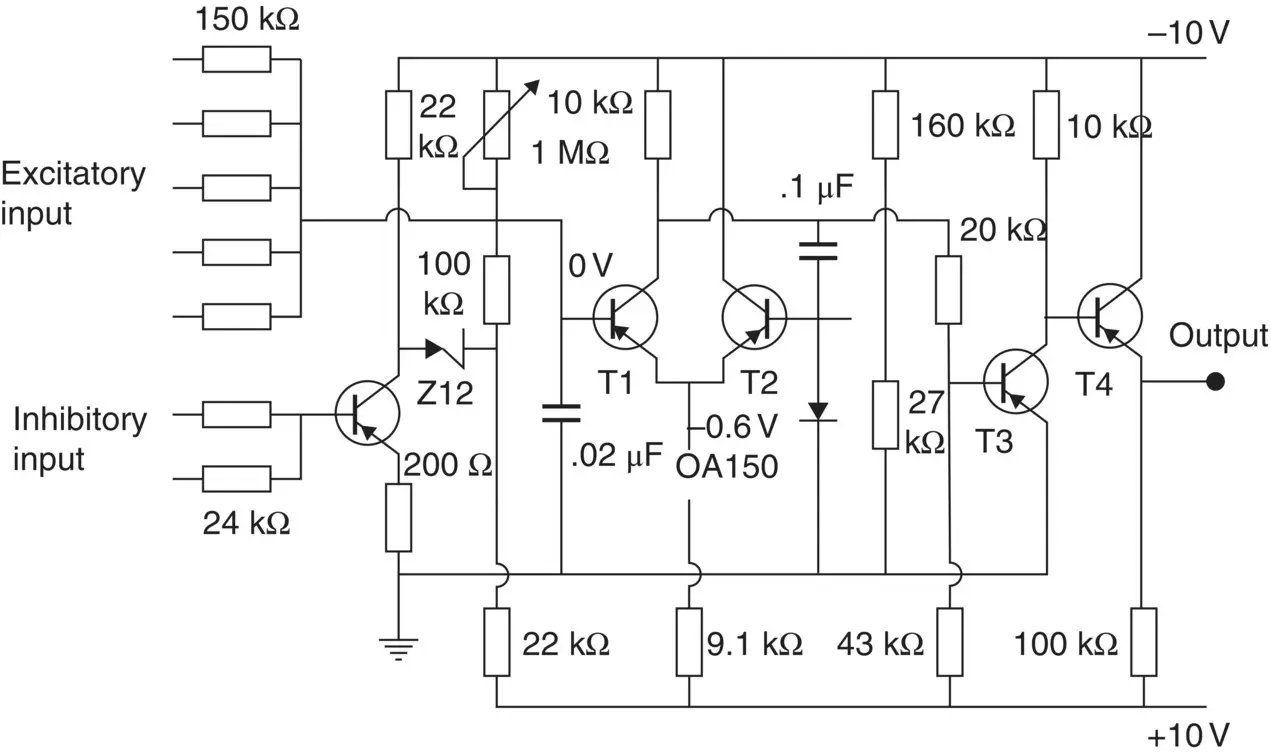
Figure 3.17 The Harmon neuron model [60].

Figure 3.18 The Lewis model for simulation of the propagation of the action pulse [57].

Lewis simulated the propagation of an action pulse in a uniform axon and obtained interesting results [57]. The model structure, illustrated in Figure 3.18, can be seen to include a network of membrane elements as well as axial resistors representing the intracellular resistance. A total of six membrane elements are depicted in the figure. The model is an electronic realization of the linear core‐conductor model with active membrane elements. An approximation of an AP is generated in the output of each membrane element.

Mahowald et al. [61] used electronic neuron models or neuron‐like circuits as processing elements for electronic computers, called neurocomputers. Two examples of these models are as follows. The electronic neuron model developed by [62] is realized with integrated circuit technology. The circuit includes one neuron with eight synapses. The chip area of the integrated circuit is 4.5 × 5 mm 2. The array contains about 200 NPN and 100 PNP transistors, and about 200 of them are used. In 1991, Mahowald and Douglas [63] published an integrated circuit realization of electronic neuron model. The model was realized with complementary metal oxide semiconductor (CMOS) circuits using very large‐scale integrated (VLSI) technology. Their model accurately simulates the spikes of a neocortical neuron. The power dissipation of the circuit is 60 μW, and it occupies less than 0.1 mm 2. It is estimated that 100–200 such neurons could be fabricated on a 1 cm × 1 cm die.

Neuron threshold is the transmembrane voltage level at which any further depolarization will activate a sufficient number of sodium channels to enter a self‐generative positive feedback phase [64]. This threshold is often considered constant. Any alteration to the threshold influences the neuron spike train temporal transformation. There are however evidences that the threshold is nonlinearly affected by the AP firing history [65–67]. In [64] a method for dynamically varying the threshold for intercellular activity has been proposed. The method is suitable for systems with spikes in both their inputs and outputs.

Most of the models generated mathematically are very primitive representations of EEG generators. More complicated models will be necessary to represent the brain EPs and the abnormal EEGs recorded under various brain diseases and disorders. The model based on phase coupling explained here introduces the WCOs which can be used to model the interactions between the neurons. Hodgkin and Huxley model conversely provides a detailed and accurate model for generation of active potentials. Linear and nonlinear prediction filers can be used in modelling the neuro generators. Gaussian mixtures are capable in modelling the EEG particularly event‐related, evoked, and movement‐related potentials. Finally, circuit models have been introduced to combine the excitatory and inhibitory post‐synaptic potentials for generation of an EEG signal. The synaptic currents have also been modelled using electronic circuits. These circuits can be expanded to have very accurate model of either a single neuron or a membrane. They can also be used to model a large number of neurons for generation of particular brain waveforms. The electronic models have potential to be used in brain morphing technology.