The amount of heat generated in the tissue depends on the current density and the tissue conductivity. However, the conductivity is in turn determined by the heat generated in the tissue; since the tissue ionic conductivity increases with the increasing temperature, a further intensification in current density and temperature occurs. Thus, the thermal injury is determined as the result of a feedback mechanism; however, the conductivity change is not considered in burn models due to the complexity of the resulting nonlinear equations.
w delivered by a current i during the time t to a homogeneous volume of biological tissue of length l , cross-sectional area and ionic conductivity σ ( Eq. 1.2), it is conservatively assumed an adiabatic process. Such a process calls for no heat removal into neighboring tissues by blood flow or by conduction and/or convection into the air, but it is presumed that all the heat stays within the tissue.
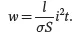 (1.2)
(1.2)
Vues of ionic conductivity of some biological tissues are listed in Table 1.3[12].
Table 1.3 Electrical conductivity σ of biological tissues
| Tissue |
σ (S/m) |
| Blood |
7.00E-1 |
| Bone |
8.07E-2 |
| Cartilage |
1.71E-1 |
| Fat |
4.04E-2 |
| Heart |
8.27E-2 |
| Kidney |
8.92E-2 |
| Muscle |
2.33E-1 |
| Nerve |
2.74E-2 |
| Skin (dry) |
2.00E-4 |
| Skin (wet) |
4.27E-4 |
The thermal injury will depend on the duration t of the contact and the temperature rise ΔT that the passing current will impose [19]. The thermal energy expressed in Eq. 1.2is related to the temperature rise ΔT to which the volume of tissue is subjected. We can write the thermal balance equation ( Eq. 1.3), which describes the exchange of heat between the heat delivered w and the heat accumulated in the volume of tissue, assuming σ independent of the temperature.
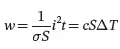 (1.3)
(1.3)
c is the volume-specific heat capacity, defined as the heat necessary to increase the temperature of a unit volume of a substance by 1˚C.
The temperature rise ΔT is given by Eq. 1.4
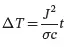 (1.4)
(1.4)
Equation 1.4shows that the temperature rise ΔT depends on the square of the current density J and on the duration t of the current circulation.
The skin has the lowest conductivity among the biological tissues, and the current density is higher at the point of contacts on the body (referred to as entry and exit sites); therefore, for a given current, the highest temperature rise is achieved on the skin, which therefore suffers the greatest level of damage.
Thermal injury of the human skin occurs when the temperature rise persists for a sufficient length of time: for instance, to cause cutaneous injury, a temperature of the skin of 45°C requires a contact duration of 2 h; 51°C requires a contact duration of 2 min; and 60°C requires a contact duration of 3 s 4Current densities of a few mA/mm 2for a duration of about 0.5 to 1 s can cause burns, whereas a current density of a few tens of mA/mm 2for a few seconds, will cause third-degree burns with destruction of deeper tissues and possible necrosis.
Thermal shock can also be caused by the heat released by electric arcs, which are accompanied by the vaporization of metal to form a superheated toxic gas.
1.5 Heated Surfaces of Electrical Equipment and Contact Burn Injuries
Burns can also be triggered by unintentional contact with hot surfaces of electrical equipment, which may be readily accessible during normal operations (e.g., the surface of a PV module) [20, 21].
According to Stevens’ Law, the perception of temperature is also superlinear with the stimulus, as varies as the 1.6 power of the temperature (i.e., experimentally analyzed by using a heated metal on a person’s arm).
Most apparatus and appliances in industrial, commercial, and residential environments are thermally insulated unless the insulation would prevent their functions (e.g., the bottom surface of a flatiron). However, superficial temperatures of insulated equipment may still be high enough to cause burns from contact with readily accessible parts. The severity of such burns will depend on the thermal resistivity of the material of the touchable surface, and the pressure and duration of the contact.
An effective protection against burns can be established based on the acceptable contact period and on the level of acceptable injury.
According to the CENELEC Guide 29 5for adults, a minimum contact period ranging between 0.5 s and 1 s should be used, based on the type of the equipment and where they are to be used (e.g., restrictive locations); however, extended reaction times may be considered based on the age of users that may possibly come into contact with the hot surface ( Table 1.4).
Table 1.4 Standard contact durations
| Age Group |
Exposure time (s) |
| Adults |
0.5–1 |
| age < 2 years |
15 |
| 2 years < age < 6 years |
4 |
| 6 years < age < 14 years |
2 |
| Elderly persons |
1–4 |
| Physical disabilities |
According to nature of disability |
Once the maximum operating temperature of readily accessible surfaces is determined, by direct measurement or calculation, the potential injury level may be established through the graph of Figure 1.7, which shows the relationship between surface temperature and exposure time.
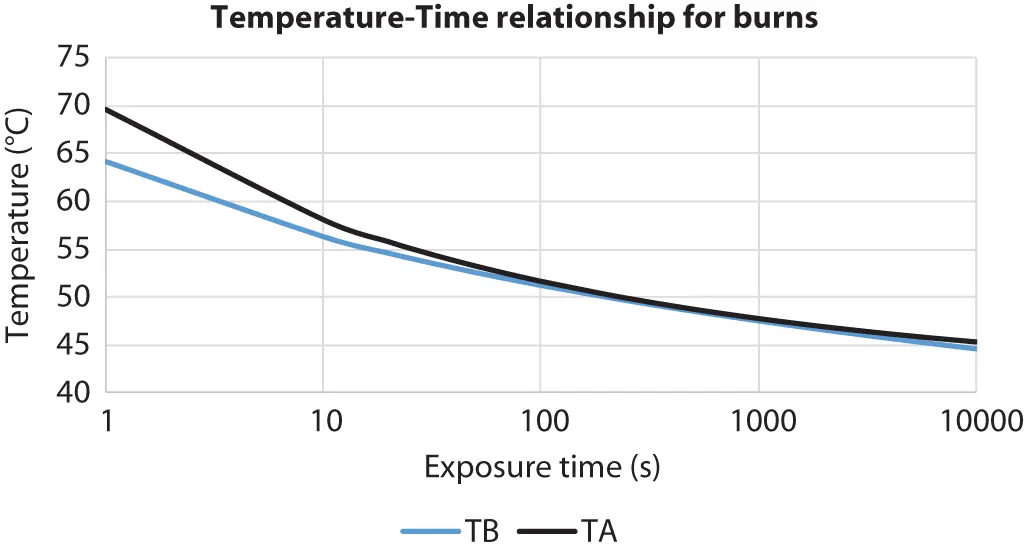
Figure 1.7 Temperature–Time Relationship for burns.
The bottom curve T Bis the locus of the pairs temperature and exposure time representing the limit of the reversible epidermal injury; T Bdescribes the acceptable injury level as a first degree burn, that is, a burn where the temperature and/or duration are not sufficient to cause necrosis of the epidermis but only reddening of the skin. T Ais the locus representing the complete trans-epidermal necrosis.
The surface of photovoltaic arrays in full sun can exceed the ambient temperature by 30°C or more, which may easily produce temperature greater than 60˚C. It is therefore apparent that PV modules’ surface with temperatures exceeding 64˚C can only be contacted for 1 s before skin injury occurs.
IEC 60364-4-42 6requires that accessible parts of electrical equipment within arm’s reach do not attain temperatures exceeding the limits given in Table 1.8, to prevent burns caused by contact with heated surfaces.
Table 1.8 Temperature limits in normal service for accessible parts of equipment
| Accessible parts |
Material of accessible surfaces |
Maximum temperatures(°C) |
| A hand-held part |
Metallic |
55 |
| Non-metallic |
65 |
| A part intended to be touched but not hand-held |
Metallic |
70 |
| Non-metallic |
80 |
| A part that does not need to be touched for normal operation |
Metallic |
80 |
| Non-metallic |
90 |
The above temperature limits vary according to whether the part is intended to be hand-held or touched during normal use, and are based on the nature of the material of the accessible surface; they do not apply to equipment for which a maximum temperature is specified in the relevant product standard.
Читать дальше

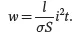 (1.2)
(1.2)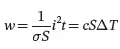 (1.3)
(1.3)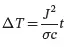 (1.4)
(1.4)











