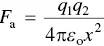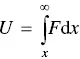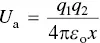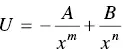For two atoms with discrete charges (that is, ions) of opposite sign such as the sodium ion (Na +) and the chlorine ion (Cl −) that form an ionic bond in the sodium chloride (NaCl) molecule, for example, this is simply an electrostatic or Coulombic attraction. The attractive force is given by
(2.1) 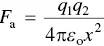
where, q 1and q 2are the electrical charges of the two ions and ε ois the permittivity of free space.
On the other hand, for atoms that are bound together by covalent bonds, F aresults from sharing of electrons. The simplest example of covalent bonding is between two hydrogen (H) atoms to form a hydrogen molecule (H 2) ( Figure 2.2). Proximity of the two atoms leads to the creation of a new electron orbital shared by the two atoms into which the two electrons go. This sharing of electrons leads to a reduction in energy and to the formation of a bond. The reduction of energy can be described in terms of an attractive force between the nuclei and shared electrons of the two atoms. In the metallic bond, the attractive force results from the attraction between the positive metal ions and a “sea” of freely moving valence electrons.
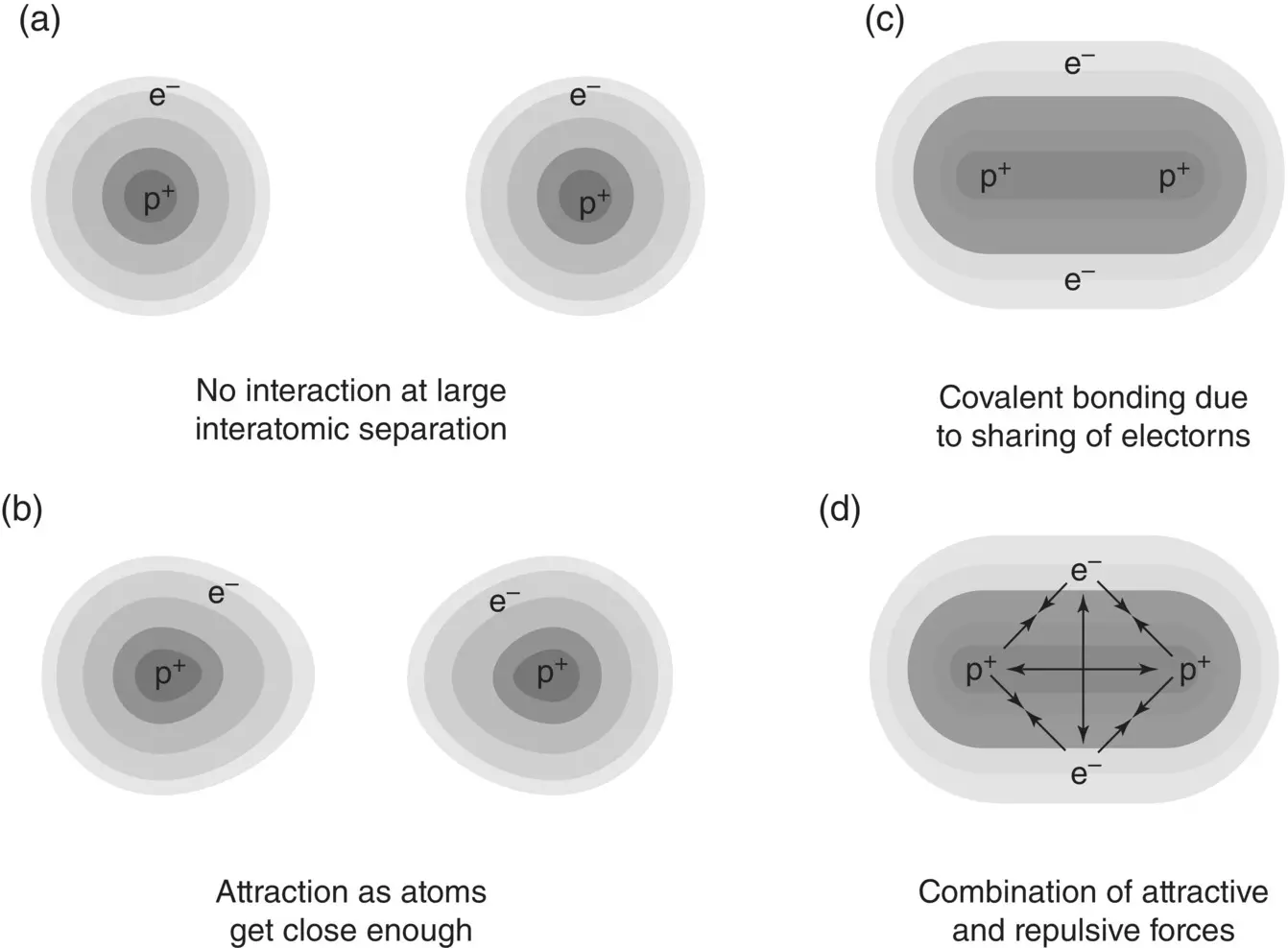
Figure 2.2 Schematic illustration of covalent bonding in the hydrogen molecule (H 2), showing the combination of attractive and repulsive forces.
For all types of bonding, F aincreases as x decreases ( Eq. (2.1)) but when x becomes sufficiently small and the electron cloud surrounding each atom starts to overlap, a repulsive force F rdevelops between the atoms. This repulsive force is more than just an electrostatic repulsion between the electron clouds of the two atoms. It has a quantum mechanical component that is rooted in the Pauli exclusion principle and another component that arises from repulsion between the atomic nuclei due to reduced screening of their charge by the overlapping electron cloud. These forces are illustrated in Figure 2.2for the hydrogen molecule.
Overall, then, the interatomic force consists of two types of forces, an attractive force F aand a repulsive force F r, both of which increase in magnitude with decreasing separation distance x between the two atoms. Analyses show that F rincreases more strongly with decreasing x than F a. The net or resultant interatomic force F is the sum of F aand F r. Figure 2.3a is a schematic of F a, F r, and F as a function of x . Conventionally, the attractive force and repulsive force are taken to be positive and negative in sign, respectively. Whereas their exact shape depends on the type of bonding (that is, ionic, covalent, or metallic bonding), the curves show the same trend qualitatively regardless of the bond type. As x decreases, F increases, reaches a maximum, and decreases rapidly thereafter.
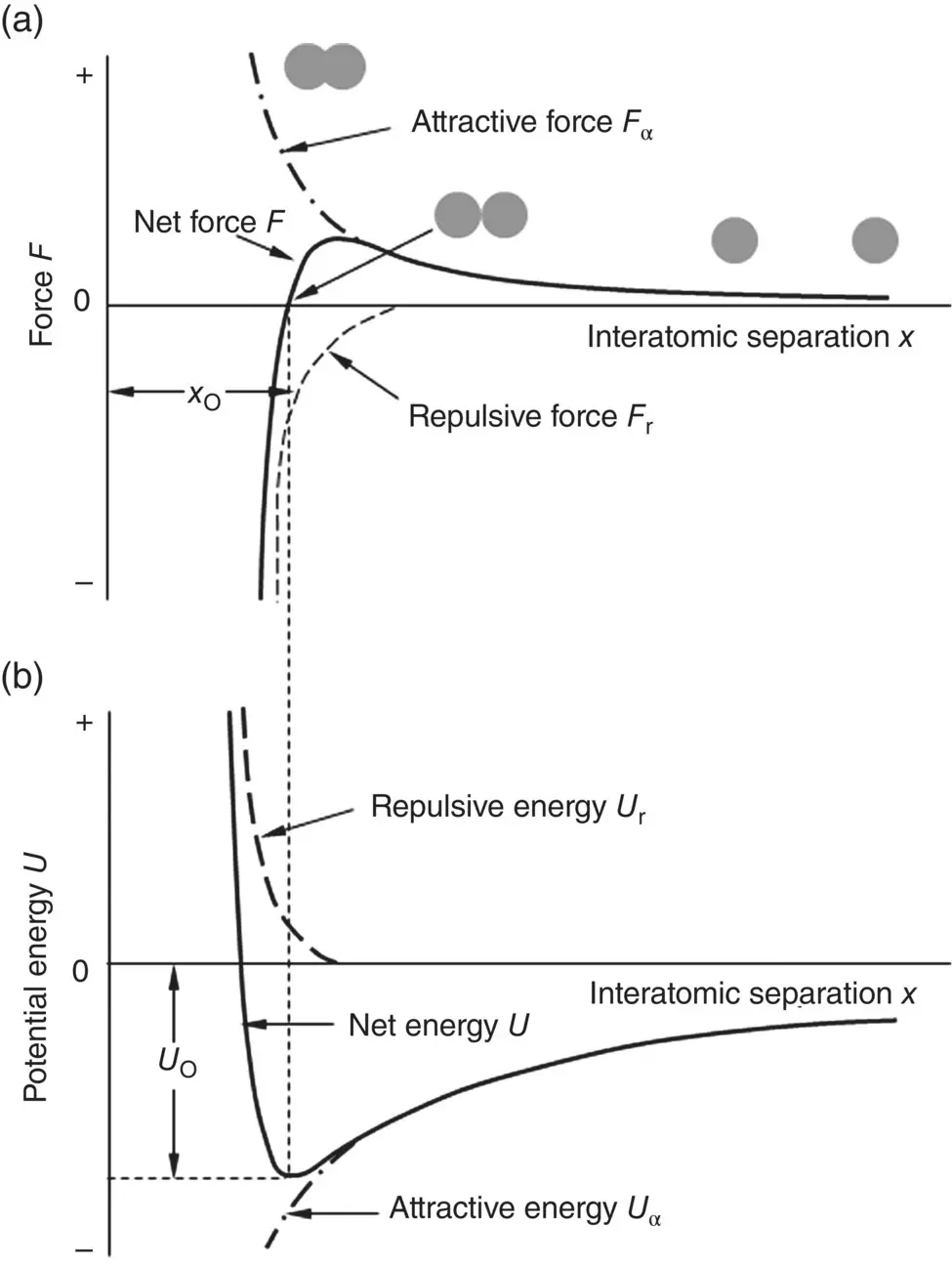
Figure 2.3 Formation of an interatomic bond viewed in terms of (a) interatomic force and (b) potential energy of interaction.
Instead of the interatomic force, it is often more convenient to describe bonding between two atoms in terms of their potential energy of interaction. This potential energy represents the work done in bringing the two atoms from infinity to a separation distance x . Representation of interatomic bonding in terms of potential energy U is equivalent to that of force F as they are related by the expression
(2.2) 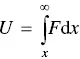
Substituting for F from Eq. (2.1), we find that for the ionic bond, the attractive potential energy is
(2.3) 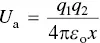
As shown in Figure 2.3b, U decreases as x decreases (that is, it becomes more negative), reaches a minimum, and increases rapidly as x continues to decrease. Analyses show that U can be described by an equation of the form
(2.4) 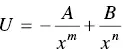
where, A and B are numerical constants and the exponent m is often far smaller than n . In ionic bonding, the first term on the right hand side of Eq. (2.4)is given by Eq. (2.3). For this type of bonding, a correction should be made to take into account the energy required to form the ions from the atoms in the first place, but this is neglected in Figure 2.3b. It is also noticed that the sign convention for potential energy is the opposite of that for the force, that is, the potential energy is taken to be negative and positive in sign, respectively, for attractive and repulsive interactions.
The parameter x o, the interatomic separation when the net force F = 0, is the equilibrium separation between the two atoms and represents the bond length ( Figure 2.3). The minimum energy U ois the bonding energy of the two atoms and is a measure of the bond strength. It gives the energy required to separate the atoms from their equilibrium spacing to an infinite distance apart. The deeper the well, the more stable the molecule and the larger the amount of energy required to separate the two atoms.
Relationship of Interatomic Force and Bonding Energy to Properties of Materials
As we go from two atoms to solid materials composed of a large number of atoms, the bond length, interatomic force, and bonding energy will be modified by the way the atoms arrange themselves and by their nearest atomic neighbors. Nevertheless, the representations of the interaction between two atoms in Figure 2.3in terms of interatomic force and bonding energy provide a useful way to understand how many of the intrinsic properties of a material arise. The shape and depth of the potential energy curve, in particular, define various properties.
Molecules with large bonding energy typically exist as solids. Furthermore, the melting point of these solids typically increase as the depth of the potential well increases. This is because a larger amount of energy, in the form of heat, is required to break the interatomic bonds and convert the material from a solid to a liquid ( Table 2.2). The elastic modulus is a measure of a material’s stiffness, that is, its ability to initially deform when subjected to a mechanical load. It is proportional to the slope of the F versus x curve at x = x o( Figure 2.4). A steep slope represents a strongly bonded material with high elastic modulus whereas a gradual slope represents a weakly bonded material with low elastic modulus ( Table 2.3).
Table 2.2 Bonding energy and melting temperature of various substances.
| Type of bond |
Substance |
Bonding energy |
Melting temperature (°C) |
| kJ/mol |
eV per atom, ion or molecule |
| Ionic |
NaCl |
640 |
3.3 |
801 |
| MgO |
1000 |
5.2 |
2800 |
| Covalent |
Si |
450 |
4.7 |
1410 |
| C (diamond) |
713 |
7.4 |
>3550 |
| Metallic |
Hg |
68 |
0.7 |
−39 |
| Al |
324 |
3.4 |
660 |
| Fe |
406 |
4.2 |
1538 |
| W |
849 |
8.8 |
3410 |
| Van der Waals |
Ar |
7.7 |
0.08 |
−189 |
| Cl 2 |
31 |
0.32 |
−101 |
| Hydrogen |
NH 3 |
35 |
0.36 |
−78 |
| H 2O |
51 |
0.52 |
0 |
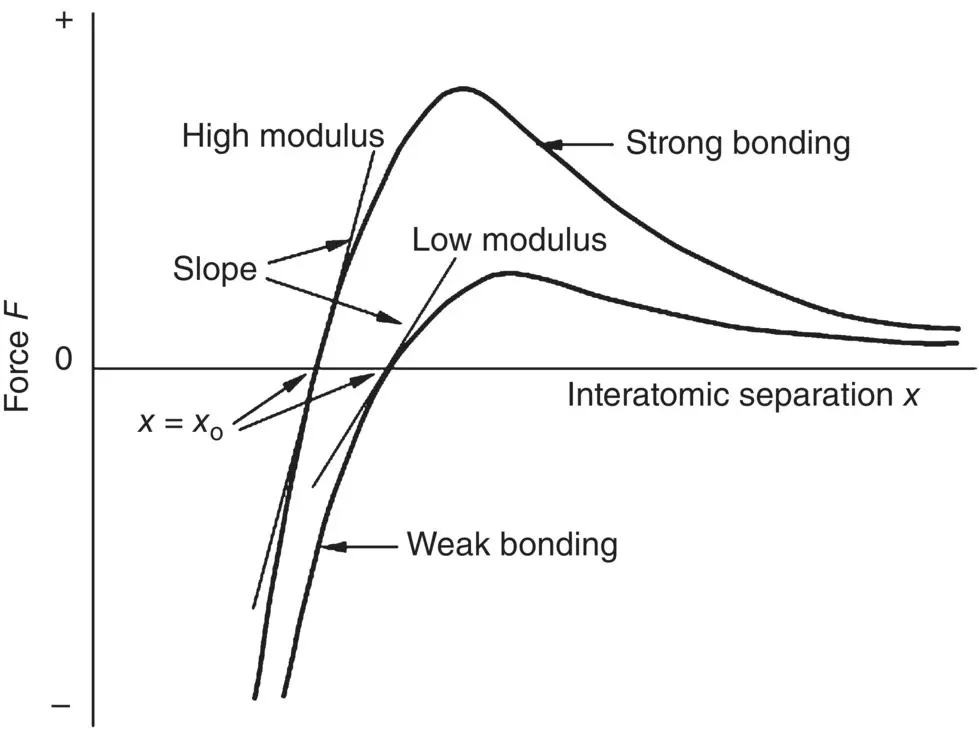
Figure 2.4 Relationship between interatomic force versus displacement curve and the Young’s modulus of a solid.
Читать дальше