Vahid Mirjalili - Python Machine Learning

El equilibrio entre el descenso de gradiente en lotes y el descenso de gradiente estocástico se denomina aprendizaje de minilote. El aprendizaje de minilote puede ser entendido como la aplicación de un descenso de gradiente en lote a subconjuntos más pequeños de datos de entrenamiento; por ejemplo, 32 muestras a la vez. La ventaja sobre el descenso de gradiente en lote es que la convergencia se consigue más rápido mediante minilotes gracias a que las actualizaciones de peso son más frecuentes. Además, el aprendizaje de minilote nos permite sustituir el bucle for en las muestras de entrenamiento en el descenso de gradiente estocástico con operaciones vectorizadas, que pueden mejorar aún más la eficiencia computacional de nuestro algoritmo de aprendizaje.

Como ya hemos implementado la regla de aprendizaje Adaline con un descenso de gradiente, solo necesitamos realizar algunos ajustes para modificar el algoritmo de aprendizaje y actualizar los pesos mediante el descenso de gradiente estocástico. Dentro del método fit, actualizaremos los pesos después de cada muestra de aprendizaje. Además, implementaremos un método partial_fit adicional, que no reiniciará los pesos, para el aprendizaje online. Con el fin de comprobar si nuestro algoritmo converge después del entrenamiento, vamos a calcular el coste como el coste medio de las muestras de entrenamiento en cada época. Además, añadiremos una opción para mezclar los datos de entrenamiento antes de cada época y evitar así ciclos repetitivos cuando estemos optimizando la función de coste. A través del parámetro random_state permitimos la especificación de una semilla aleatoria para la reproducibilidad:

class AdalineSGD(object):

"""ADAptive LInear NEuron classifier.

Parameters

------------

eta : float

Learning rate (between 0.0 and 1.0)

n_iter : int

Passes over the training dataset.

shuffle : bool (default: True)

Shuffles training data every epoch if True

to prevent cycles.

random_state : int

Random number generator seed for random weight

initialization.

Attributes

-----------

w_ : 1d-array

Weights after fitting.

cost_ : list

Sum-of-squares cost function value averaged over all

training samples in each epoch.

"""

def __init__(self, eta=0.01, n_iter=10,

shuffle=True, random_state=None):

self.eta = eta

self.n_iter = n_iter

self.w_initialized = False

self.shuffle = shuffle

self.random_state = random_state

def fit(self, X, y):

""" Fit training data.

Parameters

----------

X : {array-like}, shape = [n_samples, n_features]

Training vectors, where n_samples is the number

of samples and

n_features is the number of features.

y : array-like, shape = [n_samples]

Target values.

Returns

-------

self : object

"""

self._initialize_weights(X.shape[1])

self.cost_ = []

for i in range(self.n_iter):

if self.shuffle:

X, y = self._shuffle(X, y)

cost = []

for xi, target in zip(X, y):

cost.append(self._update_weights(xi, target))

avg_cost = sum(cost) / len(y)

self.cost_.append(avg_cost)

return self

def partial_fit(self, X, y):

"""Fit training data without reinitializing the weights"""

if not self.w_initialized:

self._initialize_weights(X.shape[1])

if y.ravel().shape[0] > 1:

for xi, target in zip(X, y):

self._update_weights(xi, target)

else:

self._update_weights(X, y)

return self

def _shuffle(self, X, y):

"""Shuffle training data"""

r = self.rgen.permutation(len(y))

return X[r], y[r]

def _initialize_weights(self, m):

"""Initialize weights to small random numbers"""

self.rgen = np.random.RandomState(self.random_state)

self.w_ = self.rgen.normal(loc=0.0, scale=0.01,

size=1 + m)

self.w_initialized = True

def _update_weights(self, xi, target):

"""Apply Adaline learning rule to update the weights"""

output = self.activation(self.net_input(xi))

error = (target - output)

self.w_[1:] += self.eta * xi.dot(error)

self.w_[0] += self.eta * error

cost = 0.5 * error**2

return cost

def net_input(self, X):

"""Calculate net input"""

return np.dot(X, self.w_[1:]) + self.w_[0]

def activation(self, X):

"""Compute linear activation"""

return X

def predict(self, X):

"""Return class label after unit step"""

return np.where(self.activation(self.net_input(X))

>= 0.0, 1, -1)

El método _shuffle que estamos utilizando ahora en el clasificador AdalineSGD funciona del siguiente modo: a través de la función permutation en np.random generamos una secuencia aleatoria de números únicos en el rango de 0 a 100. Estos números se pueden utilizar después como índice para mezclar nuestra matriz de características y el vector de etiqueta de clase.

Podemos utilizar el método fit para entrenar el clasificador AdalineSGD y el método plot_decision_regions para representar los resultados del entrenamiento:

>>> ada = AdalineSGD(n_iter=15, eta=0.01, random_state=1)

>>> ada.fit(X_std, y)

>>> plot_decision_regions(X_std, y, classifier=ada)

>>> plt.title('Adaline - Stochastic Gradient Descent')

>>> plt.xlabel('sepal length [standardized]')

>>> plt.ylabel('petal length [standardized]')

>>> plt.legend(loc='upper left')

>>> plt.show()

>>> plt.plot(range(1, len(ada.cost_) + 1), ada.cost_, marker='o')

>>> plt.xlabel('Epochs')

>>> plt.ylabel('Average Cost')

>>> plt.show()

Los dos diagramas que obtenemos de la ejecución del ejemplo de código anterior se muestran en la siguiente imagen:

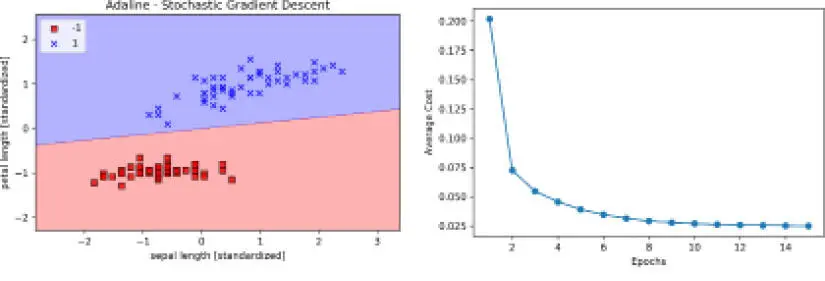
Como podemos ver, el coste medio disminuye con gran rapidez, y el límite de decisión final después de 15 épocas se asemeja al descenso de gradiente en lotes Adaline. Si queremos actualizar nuestro modelo –por ejemplo, en un caso de aprendizaje online con transmisión de datos– podríamos llamar simplemente el método partial_fit sobre muestras individuales: ada.partial_fit(X_std[0, :], y[0]).

Resumen

En este capítulo, hemos podido conocer los conceptos básicos de los clasificadores lineales para el aprendizaje supervisado. Después de haber implementado un perceptrón, hemos visto cómo podemos entrenar neuronas lineales adaptativas de manera eficiente mediante la implementación vectorizada del descenso de gradiente, y el aprendizaje online mediante el descenso de gradiente estocástico.

Ahora que hemos visto cómo implementar clasificadores simples en Python, ya estamos preparados para pasar al siguiente capítulo, donde utilizaremos la librería de aprendizaje automático de Python scikit-learn para tener acceso a clasificadores de aprendizaje automático más potentes y avanzados que se utilizan habitualmente tanto en formación como en industria. El enfoque orientado a objetos que hemos utilizado para implementar los algoritmos del perceptrón y Adaline nos ayudará a entender el API scikit-learn, cuya implementación se basa en los mismos conceptos principales que hemos utilizado en este capítulo: los métodos fit y predict. Basándonos en estos conceptos, aprenderemos sobre la regresión logística para modelar probabilidades de clase y máquinas de vectores de soporte para trabajar con límites de decisión no lineales. Además, presentaremos una clase distinta de algoritmos de aprendizaje supervisado: algoritmos basados en árboles, que habitualmente se combinan en clasificadores de conjuntos robustos.