xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
np.arange(x2_min, x2_max, resolution))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.3, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
# representar muestras de clase
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y == cl, 0],
y=X[y == cl, 1],
alpha=0.8,
c=colors[idx],
marker=markers[idx],
label=cl,
edgecolor='black')
En primer lugar, definimos un número de colors y markers y creamos un mapa de colores a partir de la lista de colores a través de ListedColormap. A continuación, determinamos los valores mínimos y máximos para las dos características y utilizamos los vectores de características para crear un par de matrices de cuadrícula xx1 y xx2 mediante la función meshgrid de NumPy. Como hemos entrenado nuestro clasificador de perceptrón en dos dimensiones de características, necesitamos acoplar las matrices y crear una matriz que tenga el mismo número de columnas que el subconjunto de entrenamiento Iris. Para ello, podemos utilizar el método predict para predecir las etiquetas de clase Z de los correspondientes puntos de la cuadrícula. Después de remodelar las etiquetas de clase Z predichas en una cuadrícula con las mismas dimensiones que xx1 y xx2, ya podemos dibujar un diagrama de contorno con la función contourf de Matplotlib, que mapea las diferentes regiones de decisión en distintos colores para cada clase predicha en la matriz de cuadrícula:
>>> plot_decision_regions(X, y, classifier=ppn)
>>> plt.xlabel('sepal length [cm]')
>>> plt.ylabel('petal length [cm]')
>>> plt.legend(loc='upper left')
>>> plt.show()
Después de ejecutar el ejemplo de código anterior, deberíamos ver un diagrama de las regiones de decisión, como se muestra en la siguiente figura:
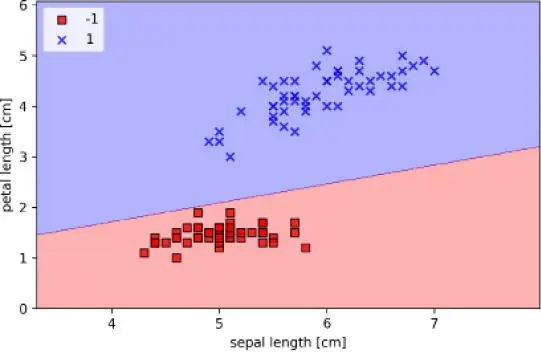
Como podemos ver en el diagrama, el perceptrón ha aprendido un límite de decisión capaz de clasificar perfectamente todas las muestras de flor en el subconjunto de entrenamiento Iris.
 |
 |
Aunque el perceptrón ha clasificado a la perfección las dos clases de flor Iris, la convergencia es uno de los mayores problemas del perceptrón. Frank Rosenblatt probó matemáticamente que la regla de aprendizaje del perceptrón converge si las dos clases pueden ser separadas por un hiperplano lineal. Sin embargo, si las clases no pueden ser separadas perfectamente por un límite de decisión lineal, los pesos no dejarán nunca de actualizarse a menos que indiquemos un número máximo de épocas. |
 |
Neuronas lineales adaptativas y la convergencia del aprendizaje
En esta sección, echaremos un vistazo a otro tipo de red neuronal de capa única: las neuronas lineales adaptativas, en inglés ADAptive LInear NEuron (Adaline). Adaline fue publicada por Bernard Widrow y su alumno Ted Hoff, pocos años después del algoritmo de perceptrón de Frank Rosenblatt, y puede considerarse como una mejora de este último. (Puedes consultar An Adaptive "Adaline" Neuron Using Chemical "Memistors", Technical Report Number 1553-2, B. Widrow and others, Stanford Electron Labs, Stanford, CA, October 1960).
El algoritmo Adaline es especialmente interesante porque ilustra los conceptos clave para definir y minimizar las funciones de coste continuas. Esto sienta las bases para la comprensión de algoritmos de aprendizaje automático más avanzados para la clasificación, como la regresión logística, máquinas de vectores de soporte y modelos de regresión, que trataremos en capítulos posteriores.
La diferencia clave entre la regla Adaline (también conocida como regla Widrow-Hoff) y el perceptrón de Rosenblatt es que los pesos se actualizan en base a una función de activación lineal en vez de en base a una función escalón unitario como sucede en el perceptrón. En Adaline, esta función de activación lineal 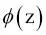 es simplemente la función de identificación de la entrada de red, por lo que:
es simplemente la función de identificación de la entrada de red, por lo que:
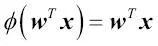
Mientras que la función de activación lineal se utiliza para aprender los pesos, seguimos utilizando una función de umbral que realiza la predicción final, que es parecida a la función escalón unitario que hemos visto anteriormente. Las diferencias principales entre el perceptrón y el algoritmo Adaline se encuentran destacadas en la siguiente imagen:
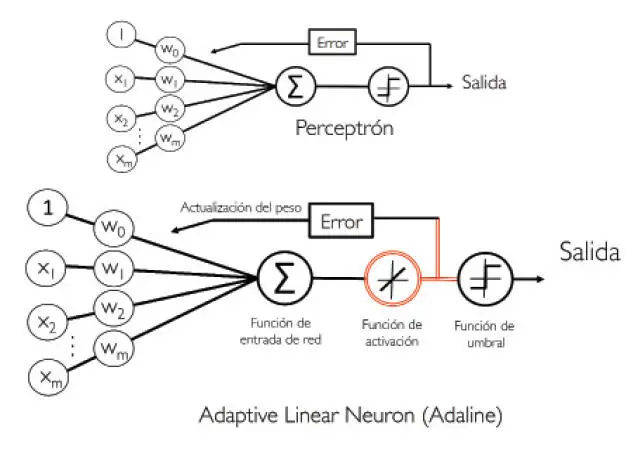
Esta ilustración muestra que el algoritmo Adaline compara las etiquetas de clase verdaderas con la salida de valores continuos de la función de activación lineal para calcular el error del modelo y actualizar los pesos. Por el contrario, el perceptrón compara las etiquetas de clase verdaderas con las etiquetas de clase predichas.
Minimizar funciones de coste con el descenso de gradiente
Uno de los ingredientes clave de los algoritmos de aprendizaje automático supervisado es una función objetivo definida que debe ser optimizada durante el proceso de aprendizaje. Esta función objetivo suele ser una función de coste que queremos minimizar. En el caso de Adaline, podemos definir la función de coste 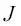 para aprender los pesos como la Suma de Errores Cuadráticos (SSE, del inglés Sum of Squared Errors) entre la salida calculada y la etiqueta de clase verdadera:
para aprender los pesos como la Suma de Errores Cuadráticos (SSE, del inglés Sum of Squared Errors) entre la salida calculada y la etiqueta de clase verdadera:
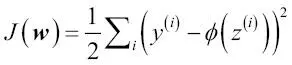
Hemos añadido el término 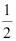 simplemente para facilidad nuestra, porque nos permitirá derivar el gradiente de un modo más fácil, como veremos en los siguientes párrafos. La principal ventaja de esta función de activación lineal continua, en comparación con la función escalón unitario, es que la función de coste pasa a ser diferenciable. Otra propiedad a tener en cuenta de esta función de coste es que es convexa; esto significa que podemos utilizar un simple pero potente algoritmo de optimización, denominado descenso de gradiente, para encontrar los pesos que minimicen nuestra función de coste y clasificar así las muestras del conjunto de datos Iris.
simplemente para facilidad nuestra, porque nos permitirá derivar el gradiente de un modo más fácil, como veremos en los siguientes párrafos. La principal ventaja de esta función de activación lineal continua, en comparación con la función escalón unitario, es que la función de coste pasa a ser diferenciable. Otra propiedad a tener en cuenta de esta función de coste es que es convexa; esto significa que podemos utilizar un simple pero potente algoritmo de optimización, denominado descenso de gradiente, para encontrar los pesos que minimicen nuestra función de coste y clasificar así las muestras del conjunto de datos Iris.
Читать дальше



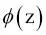 es simplemente la función de identificación de la entrada de red, por lo que:
es simplemente la función de identificación de la entrada de red, por lo que: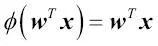

 para aprender los pesos como la Suma de Errores Cuadráticos (SSE, del inglés Sum of Squared Errors) entre la salida calculada y la etiqueta de clase verdadera:
para aprender los pesos como la Suma de Errores Cuadráticos (SSE, del inglés Sum of Squared Errors) entre la salida calculada y la etiqueta de clase verdadera: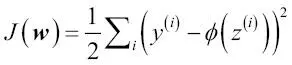
 simplemente para facilidad nuestra, porque nos permitirá derivar el gradiente de un modo más fácil, como veremos en los siguientes párrafos. La principal ventaja de esta función de activación lineal continua, en comparación con la función escalón unitario, es que la función de coste pasa a ser diferenciable. Otra propiedad a tener en cuenta de esta función de coste es que es convexa; esto significa que podemos utilizar un simple pero potente algoritmo de optimización, denominado descenso de gradiente, para encontrar los pesos que minimicen nuestra función de coste y clasificar así las muestras del conjunto de datos Iris.
simplemente para facilidad nuestra, porque nos permitirá derivar el gradiente de un modo más fácil, como veremos en los siguientes párrafos. La principal ventaja de esta función de activación lineal continua, en comparación con la función escalón unitario, es que la función de coste pasa a ser diferenciable. Otra propiedad a tener en cuenta de esta función de coste es que es convexa; esto significa que podemos utilizar un simple pero potente algoritmo de optimización, denominado descenso de gradiente, para encontrar los pesos que minimicen nuestra función de coste y clasificar así las muestras del conjunto de datos Iris.










