Vahid Mirjalili - Python Machine Learning

Para probar nuestra implementación del perceptrón, vamos a cargar dos clases de flor, Setosa y Versicolor, del conjunto de datos Iris. Aunque la regla del perceptrón no está restringida a dos dimensiones, por razones de visualización solo tendremos en cuenta las características de longitud de sépalo y longitud de pétalo. Además, por razones prácticas, elegimos solo las dos clases de flor: Setosa y Versicolor. Sin embargo, el algoritmo perceptrón se puede ampliar a una clasificación multidimensional –por ejemplo, la técnica One-versus-All (OvA)–.

OvA, a veces también llamada One-versus-Rest (OvR), es una técnica que nos permite ampliar un clasificador binario a problemas multiclase. Mediante OvA, podemos entrenar un clasificador por clase, donde cada clase individual se trata como una clase positiva y las muestras procedentes de otras clases se consideran clases negativas. Si tuviéramos que clasificar una nueva muestra de datos, utilizaríamos nuestros clasificadores n, donde n es el número de etiquetas de clase, y asignaríamos la etiqueta de clase con la fiabilidad más alta a cada muestra individual. En el caso del perceptrón, utilizaríamos OvA para elegir la etiqueta de clase asociada al mayor valor absoluto de entrada de red.

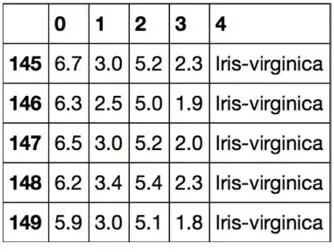
Primero, utilizaremos la librería pandas para cargar el conjunto de datos Iris directamente del UCI Machine Learning Repository dentro de un objeto DataFrame e imprimir las últimas cinco líneas mediante el método tail para comprobar que los datos se han cargado correctamente:

>>> import pandas as pd

>>> df = pd.read_csv('https://archive.ics.uci.edu/ml/'

... 'machine-learning-databases/iris/iris.data',

... header=None)

>>> df.tail()

Puedes encontrar una copia del conjunto de datos Iris (y de todos los otros conjuntos de datos utilizados en este libro) en el paquete de código de este libro, que puedes utilizar si estás trabajando offline o si el servidor UCI https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.dataestá temporalmente no disponible. Por ejemplo, para cargar el conjunto de datos Iris desde el directorio local, puedes sustituir esta línea:df = pd.read_csv('https://archive.ics.uci.edu/ml/' 'machine-learning-databases/iris/iris.data', header=None)por esta otra:df = pd.read_csv('your/local/path/to/iris.data', header=None)

A continuación, extraemos las 100 primeras etiquetas de clase que corresponden a las 50 flores Iris-setosa y a las 50 Iris-versicolor, y convertimos las etiquetas de clase en las dos etiquetas de clase enteras 1 (versicolor) y -1 (setosa) que asignamos a un vector y, donde el método de valores de un DataFrame pandas produce la correspondiente representación NumPy.

De forma similar, extraemos la primera columna de características (longitud del sépalo) y la tercera columna de características (longitud del pétalo) de las 100 muestras de entrenamiento y las asignamos a una matriz X de características, que podemos ver a través de un diagrama de dispersión bidimensional:

>>> import matplotlib.pyplot as plt

>>> import numpy as np

>>> # seleccionar setosa y versicolor

>>> y = df.iloc[0:100, 4].values

>>> y = np.where(y == 'Iris-setosa', -1, 1)

>>> # extraer longitud de sépalo y longitud de pétalo

>>> X = df.iloc[0:100, [0, 2]].values

>>> # representar los datos

>>> plt.scatter(X[:50, 0], X[:50, 1],

... color='red', marker='o', label='setosa')

>>> plt.scatter(X[50:100, 0], X[50:100, 1],

... color='blue', marker='x', label='versicolor')

>>> plt.xlabel('sepal length [cm]')

>>> plt.ylabel('petal length [cm]')

>>> plt.legend(loc='upper left')

>>> plt.show()

Después de ejecutar el ejemplo de código precedente, deberíamos ver el siguiente diagrama de dispersión:

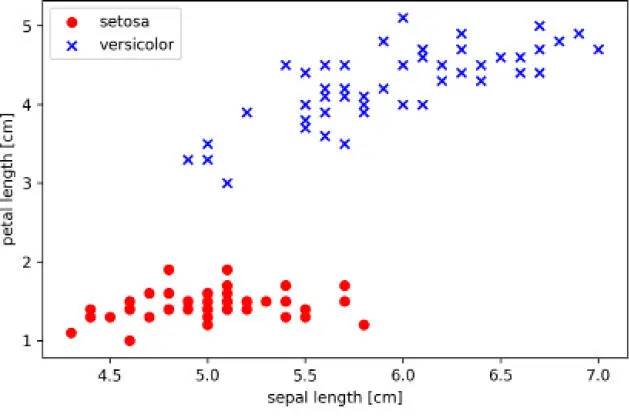
El diagrama de dispersión anterior muestra la distribución de las muestras de flor en el conjunto de datos Iris sobre los dos ejes de características, longitud del pétalo y longitud del sépalo. En este subespacio de características bidimensional, podemos ver que un límite de decisión lineal puede ser suficiente para separar flores Setosa de flores Versicolor. Por tanto, un clasificador lineal como el perceptrón podría ser capaz de clasificar las flores en este conjunto de datos perfectamente.

Ahora, ha llegado el momento de entrenar nuestro algoritmo de perceptrón en el subconjunto de datos Iris que acabamos de extraer. Además, reflejaremos en un gráfico el error de clasificación incorrecta para cada época para comprobar si el algoritmo ha convergido y encontrado un límite de decisión que separa las dos clases de flor Iris:

>>> ppn = Perceptron(eta=0.1, n_iter=10)

>>> ppn.fit(X, y)

>>> plt.plot(range(1, len(ppn.errors_) + 1),

... ppn.errors_, marker='o')

>>> plt.xlabel('Epochs')

>>> plt.ylabel('Number of updates')

>>> plt.show()

Después de ejecutar el código anterior, deberíamos ver el diagrama de los errores de clasificación incorrecta frente al número de épocas, como se muestra a continuación:

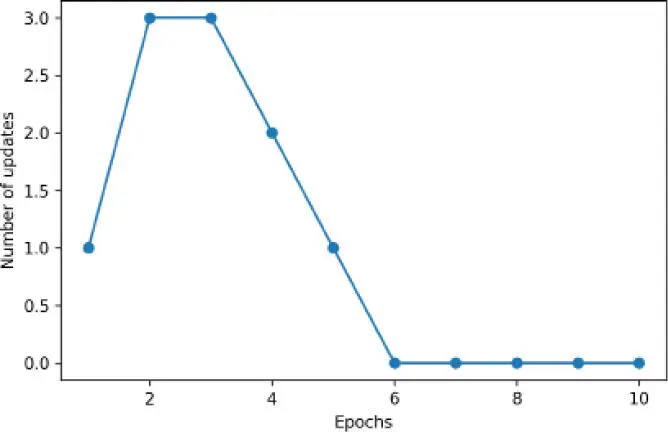
Como podemos ver en el diagrama anterior, nuestro perceptrón ha convergido después de seis épocas y debería ser capaz de clasificar perfectamente las muestras de entrenamiento. Vamos a implementar una pequeña función de conveniencia para visualizar los límites de decisión para dos conjuntos de datos bidimensionales:

from matplotlib.colors import ListedColormap

def plot_decision_regions(X, y, classifier, resolution=0.02):

# definir un generador de marcadores y un mapa de colores

markers = ('s', 'x', 'o', '^', 'v')

colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')

cmap = ListedColormap(colors[:len(np.unique(y))])

# representar la superficie de decisión

x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1

x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1