import numpy as np
class Perceptron(object):
"""Perceptron classifier.
Parameters
------------
eta : float
Learning rate (between 0.0 and 1.0)
n_iter : int
Passes over the training dataset.
random_state : int
Random number generator seed for random weight
initialization.
Attributes
-----------
w_ : 1d-array
Weights after fitting.
errors_ : list
Number of misclassifications (updates) in each epoch.
"""
def __init__(self, eta=0.01, n_iter=50, random_state=1):
self.eta = eta
self.n_iter = n_iter
self.random_state = random_state
def fit(self, X, y):
"""Fit training data.
Parameters
----------
X : {array-like}, shape = [n_samples, n_features]
Training vectors, where n_samples is the number of
samples and
n_features is the number of features.
y : array-like, shape = [n_samples]
Target values.
Returns
-------
self : object
"""
rgen = np.random.RandomState(self.random_state)
self.w_ = rgen.normal(loc=0.0, scale=0.01,
size=1 + X.shape[1])
self.errors_ = []
for _ in range(self.n_iter):
errors = 0
for xi, target in zip(X, y):
update = self.eta * (target - self.predict(xi))
self.w_[1:] += update * xi
self.w_[0] += update
errors += int(update != 0.0)
self.errors_.append(errors)
return self
def net_input(self, X):
"""Calculate net input"""
return np.dot(X, self.w_[1:]) + self.w_[0]
def predict(self, X):
"""Return class label after unit step"""
return np.where(self.net_input(X) >= 0.0, 1, -1)
Con esta implementación del perceptrón, ya podemos inicializar nuevos objetos Perceptron con un rango de aprendizaje proporcionado eta y n_iter, que es el número de épocas (pasos por el conjunto de entrenamiento). Mediante el método fit, inicializamos los pesos en self.w_ para un vector 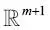 , donde m significa el número de dimensiones (características) en el conjunto de datos, al cual añadimos 1 para el primer elemento en este vector que representa el parámetro del sesgo. Recuerda que el primer elemento en este vector, self.w_[0], representa el denominado parámetro del sesgo del cual hemos hablado anteriormente.
, donde m significa el número de dimensiones (características) en el conjunto de datos, al cual añadimos 1 para el primer elemento en este vector que representa el parámetro del sesgo. Recuerda que el primer elemento en este vector, self.w_[0], representa el denominado parámetro del sesgo del cual hemos hablado anteriormente.
Observa también que este vector contiene pequeños números aleatorios extraídos de una distribución normal con desviación estándar 0.01 con rgen.normal(loc=0.0, scale=0.01, size=1 + X.shape[1]), donde rgen es un generador de números aleatorios NumPy que hemos sembrado con una semilla aleatoria especificada por el usuario, por lo que podemos reproducir, si lo deseamos, resultados previos.
La razón por la cual no ponemos los pesos a cero es que el rango de aprendizaje 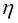 (eta) solo tiene efecto sobre el resultado de la clasificación si los pesos empiezan por valores distintos a cero. Si todos los pesos empiezan en cero, el parámetro eta del rango de aprendizaje afecta solo a la escala del vector peso, no a la dirección. Si estás familiarizado con la trigonometría, considera un vector
(eta) solo tiene efecto sobre el resultado de la clasificación si los pesos empiezan por valores distintos a cero. Si todos los pesos empiezan en cero, el parámetro eta del rango de aprendizaje afecta solo a la escala del vector peso, no a la dirección. Si estás familiarizado con la trigonometría, considera un vector 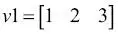 , donde el ángulo entre
, donde el ángulo entre 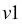 y un vector
y un vector 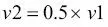 sería exactamente cero, como queda demostrado en el siguiente fragmento de código:
sería exactamente cero, como queda demostrado en el siguiente fragmento de código:
>>> v1 = np.array([1, 2, 3])
>>> v2 = 0.5 * v1
>>> np.arccos(v1.dot(v2) / (np.linalg.norm(v1) *
... np.linalg.norm(v2)))
0.0
En este caso, np.arccos es el coseno inverso trigonométrico y np.linalg.norm es una función que calcula la longitud de un vector. La razón por la cual hemos extraído los números aleatorios de una distribución normal aleatoria –en lugar de una distribución uniforme, por ejemplo– y por la que hemos utilizado una desviación estándar de 0.01 es arbitraria; recuerda que solo nos interesan valores pequeños aleatorios para evitar las propiedades de vectores todo cero, como hemos dicho anteriormente.
 |
 |
La indexación de NumPy para matrices unidimensionales funciona de forma similar a las listas de Python, utilizando la notación de corchetes ([]). Para matrices bidimensionales, el primer indexador se refiere al número de fila y el segundo al número de columna. Por ejemplo, utilizaríamos X[2, 3] para seleccionar la tercera fila y la cuarta columna de una matriz X bidimensional X. |
 |
Tras haber puesto a cero los pesos, el método fit recorre todas las muestras individuales del conjunto de entrenamiento y actualiza los pesos según la regla de aprendizaje del perceptrón tratada en la sección anterior. Las etiquetas de clase son predichas por el método predict, que es llamado en el método fit para predecir la etiqueta de clase para la actualización del peso, aunque también puede ser utilizado para predecir las etiquetas de clase de nuevos datos una vez ajustado nuestro modelo. Además, también recopilamos el número de errores de clasificación durante cada época en la lista self.errors_, de manera que posteriormente podemos analizar si nuestro perceptrón ha funcionado bien durante el entrenamiento. La función np.dot que se utiliza en el método net_input simplemente calcula el producto escalar de un vector 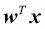 .
.
 |
 |
En lugar de utilizar NumPy para calcular el producto escalar entre dos matrices a y b mediante a.dot(b) o np.dot(a, b), también podemos realizar el cálculo con Python puro mediante sum([j * j for i, j in zip(a, b)]). Sin embargo, la ventaja de utilizar NumPy frente a las estructuras clásicas de Python for loop es que sus operaciones aritméticas son vectorizadas. La vectorización significa que una operación aritmética elemental se aplica automáticamente a todos los elementos de una matriz. Formulando nuestras operaciones aritméticas como una secuencia de instrucciones sobre una matriz, en lugar de llevar a cabo un conjunto de operaciones para cada elemento cada vez, se utilizan mejor las arquitecturas de CPU modernas con soporte SIMD (Single Instruction, Multiple Data o, en español, Una Instrucción, Múltiples Datos). Además, NumPy utiliza librerías de álgebra lineal altamente optimizadas como la Basic Linear Algebra Subprograms (BLAS) y la Linear Algebra Package (LAPACK), escritas en C o Fortran. Por último, NumPy también nos permite escribir nuestro código de un modo más compacto e intuitivo utilizando los conceptos básicos del álgebra lineal, como productos escalares de matrices y vectores. |
 |
Entrenar un modelo de perceptrón en el conjunto de datos Iris
Читать дальше

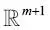 , donde m significa el número de dimensiones (características) en el conjunto de datos, al cual añadimos 1 para el primer elemento en este vector que representa el parámetro del sesgo. Recuerda que el primer elemento en este vector, self.w_[0], representa el denominado parámetro del sesgo del cual hemos hablado anteriormente.
, donde m significa el número de dimensiones (características) en el conjunto de datos, al cual añadimos 1 para el primer elemento en este vector que representa el parámetro del sesgo. Recuerda que el primer elemento en este vector, self.w_[0], representa el denominado parámetro del sesgo del cual hemos hablado anteriormente.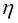 (eta) solo tiene efecto sobre el resultado de la clasificación si los pesos empiezan por valores distintos a cero. Si todos los pesos empiezan en cero, el parámetro eta del rango de aprendizaje afecta solo a la escala del vector peso, no a la dirección. Si estás familiarizado con la trigonometría, considera un vector
(eta) solo tiene efecto sobre el resultado de la clasificación si los pesos empiezan por valores distintos a cero. Si todos los pesos empiezan en cero, el parámetro eta del rango de aprendizaje afecta solo a la escala del vector peso, no a la dirección. Si estás familiarizado con la trigonometría, considera un vector 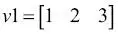 , donde el ángulo entre
, donde el ángulo entre 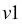 y un vector
y un vector 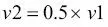 sería exactamente cero, como queda demostrado en el siguiente fragmento de código:
sería exactamente cero, como queda demostrado en el siguiente fragmento de código:


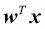 .
.