Paolo Aliverti - Electrónica para makers

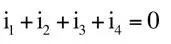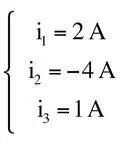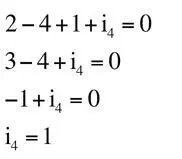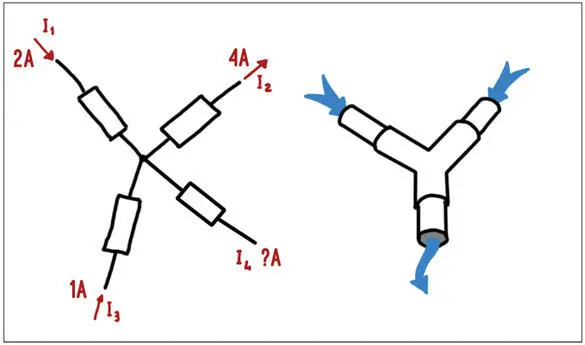
Figura 1.19 –La suma de las corrientes en un nodo siempre es igual a cero.

Podemos observar el mismo comportamiento en las corrientes: en un nodo pueden entrar o salir distintas corrientes, lo importante es que, si entra una cantidad determinada de corriente, la misma cantidad sea la que salga. En un nodo llegan cuatro cables o hilos por los cuales fluyen las corrientes: i 1, i 2, i 3, i 4. Una regla sería: la corriente que entra en el nodo es de signo positivo, mientras que si sale, el signo es negativo. La suma de todas las corrientes en el nodo siempre debe ser igual a cero.

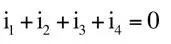
Esta fórmula se denomina Ley de corrientes de Kirchhoff. Si las corrientes de la figura 1.19 valen:

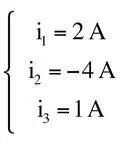
i 4se calculará del siguiente modo:

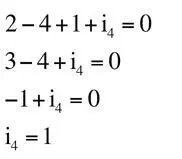
La corriente i 4es de signo positivo y, por tanto, según la regla que hemos establecido, será entrante en el nodo.

Un circuito es una red de componentes dónde podemos identificar mallas, es decir, anillos. Un anillo está formado por un camino cerrado que podemos recorrer caminando solo por los elementos del circuito: cables y componentes. Un circuito contiene varios anillos, los cuales tienen partes en común.

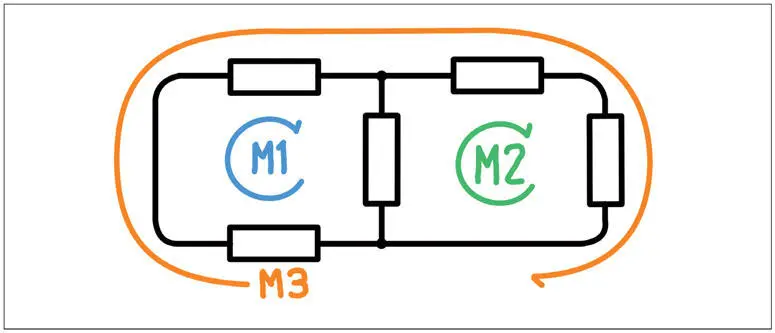
Figura 1.20 -El circuito de la figura tiene tres mallas.

La tensión en los extremos de un dipolo se puede indicar con una flecha que ayuda a identificar la polaridad, porque su punta señala el polo positivo. También podríamos medir esta tensión con un tester o un multímetro, aunque solo podremos leer algo si el componente se encuentra en un circuito y está alimentado. A menudo no se conoce el sentido de la tensión (es decir, por qué parte es positivo y por cuál, negativo), por lo que podemos sencillamente dibujar las flechas sobre los dipolos en el sentido que queramos. Si, tras haber efectuado los cálculos, resulta que la tensión tiene un valor negativo, será suficiente con girar el sentido de la flecha.

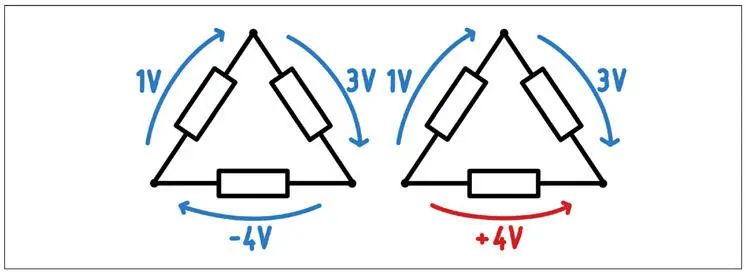
Figura 1.21 –En la primera figura, hemos dibujado primero las flechas de color azul y después hemos hecho los cálculos. De ellos se desprende que la tensión en el dipolo número tres es negativa. En la segunda figura hemos redibujado la flecha en el tercer dipolo orientada correctamente.

Existe una versión del Teorema de tensiones de Kirchhoff: si sumamos las diferencias de potencial de los lados de un anillo cualquiera, veremos que su suma es igual a cero. Esta regla vale para cualquier anillo del circuito y, de hecho, es más o menos como resolver un sudoku.

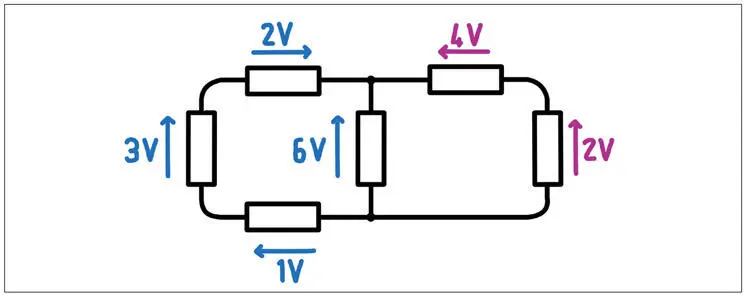
Figura 1.22 –En este circuito se han calculado las tensiones de cada dipolo. La suma de las tensiones de cada posible anillo es siempre igual a cero.

En el circuito dibujado en la figura 1.22 ya se han calculado las tensiones para cada dipolo. Así, podemos comprobar fácilmente que, en tres posibles anillos del circuito, la suma de las tensiones siempre es igual a cero.

Ahora que ya sabemos los conceptos fundamentales de corriente y tensión, vamos a intentar ponerlos en práctica estudiando un simple circuito compuesto por un resistor, un led y una batería de 9 voltios. Más adelante trataremos estos componentes. De momento, necesitamos saber que:

• el resistor es un componente que reduce la corriente que circula en un circuito;

• el resistor obstaculiza el paso de la corriente, así como un tubo con una constricción obstaculiza el paso del agua;

• un led es una especie de lámpara;

• el led tiene polaridad, por lo que, si lo conectamos al revés, no se encenderá;

• el led se alimenta con una tensión de unos 2 voltios y una corriente entre los 10 y los 20 mA;

• si no respetamos los valores de tensión y corriente para el led, corremos el riesgo de dañarlo.

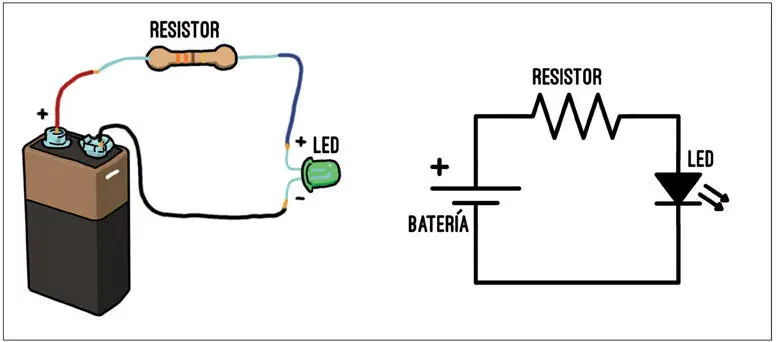
Figura 1.23 –El esquema del sencillo circuito que queremos calcular.

La pregunta que muchos se hacen cuando tienen un led entre las manos es: “¿Qué resistencia le pongo para no quemarlo?”.

Seguidamente, veamos cómo calcular la resistencia adecuada utilizando la ley de Ohm y algunas observaciones sencillas. Si conectáramos directamente el led a la batería de 9 voltios, este se encendería un instante y, después, se quemaría. El led necesita unos 2 voltios y nosotros lo hemos conectado a una batería de 9 voltios: ¡demasiados! Para encender correctamente el led, necesitamos una resistencia que hará que sobre el componente se produzca una caída de tensión de 2 voltios. Para nuestro experimento utilizaremos una batería de 9 voltios con un clip. La batería debe poder proporcionar al menos 10 miliamperios, si no el led no se encenderá, aunque esto no supone ningún problema porque una batería de 9 voltios puede proporcionar corrientes mucho mayores.

Ya hemos visto que el voltaje se puede comparar con la altura de una cascada por la que cae agua. Podemos imaginarnos la batería de 9 voltios como una cascada de 9 metros de altura y el led, como la rueda de un molino de dos metros de diámetro: se necesitará como máximo una cascada de dos metros de altura. Si situáramos el molino debajo de la cascada de 9 metros, lo destruiríamos. La resistencia sirve en este caso para romper la caída del agua de la cascada desde los 9 metros de altura. Por lo tanto, sobre la resistencia habrá una cascada de siete metros de altura.

Ahora, debemos sustituir las cascadas por las tensiones que podemos representar con flechas: por una parte, tenemos la flecha roja con los 9 voltios de la batería, juntamente con las flechas azules de los usuarios, es decir, de la resistencia y el led. Como hemos visto, la suma de las tensiones a lo largo del anillo siempre debe ser igual a cero (Kirchhoff).

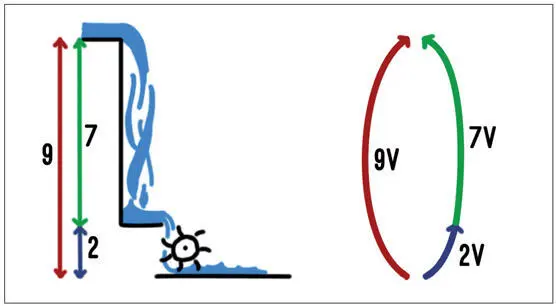
Figura 1.24 –Las tensiones están dibujadas como cascadas de agua: para no dañar el led, debemos romper la caída del agua.

En términos de voltaje, podemos observar que:

• la batería proporciona 9 voltios;

• el led necesita como máximo 2 voltios;