Reservoir Characterization

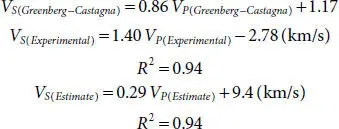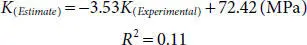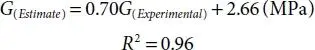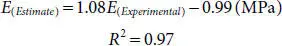
As it can be seen in Figure 2.12, the behavior of Vs-Experimental/estimated are almost independent of variability of effective pressure. While VP-Experimental/estimated increases with the rising effective pressure. The difference between rates of VP’s is because of some assumptions of Gassmann-Greenberg-Castagna equations, which they guess that media is ideal.

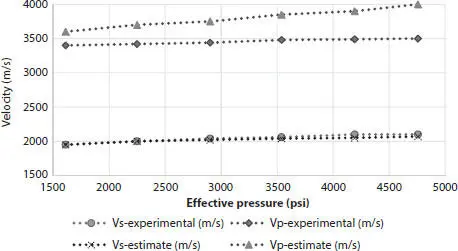
Figure 2.12 Rate of variability of experimental/estimated velocities with increasing effective pressure.

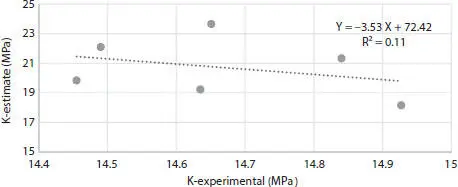
Figure 2.13 Plot of Laboratory vs. estimated Bulk modulus (K) of rock sample.

At this stage, we compared the elastic coefficients of rock samples obtained from experimental velocity values, and those estimated from Greenberg-Castagna model. According to Figure 2.13, the correlation between experimental and estimated values for volume or bulk modulus is very low and is about 0.1. This is because the compressibility of the pores media depends on the minerals type and texture of the rock. Also, it is a function of the amount and shape of media porosity. When the pores are filled with fluid, elastic modulus is affected by many parameters of fluid such as the compressibility, the kind of fluid, distribution, viscosity and also fluid incompressibility.

The fluid used in this study has a patchy saturation and has created anisotropic, heterogeneous environments. Besides that, different effective pressures that applied on a frame stone, impressed the results of Gassmann - Greenberg – Castagna equations.

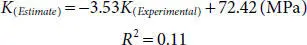
One of the assumptions of Gassmann equations is that the shear modulus in the dry and wet state is constant. It seems that this assumption is not applicable for most environments. The fact is that the changes to the texture of rock due to the reaction between rock and the fluid cause a change in the shear modulus of saturated rocks. Changes in the shear modulus is the main cause for the difference between the experimental velocity and the calculated velocity utilizing the Gassmann equations. Anyway, these differences in shear modulus cause a decrease in the use of Gassmann theory to estimate the velocity. These differences can be observed in Figure 2.14for both laboratory and estimated values. Although the correlation between experimental and estimated values are very high and close to 0.96, by replacing the common fluid and use of the estimated shear wave velocity, shear modulus values change a little as well. The reason behind this phenomenon is the defect in the Gassmann hypothesis that the shear modulus for rock is equal in both dry and saturated conditions. The reaction between the fluid and the texture of the rock is consequently causing a change in the shear modulus of saturated rocks.

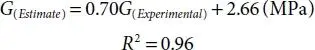
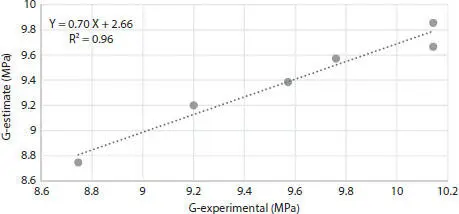
Figure 2.14 Plot of laboratory vs. estimated shear modulus.

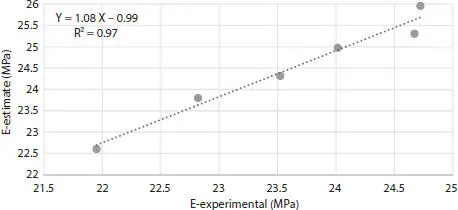
Figure 2.15 Plot of laboratory vs. estimated Young’s modulus.

But based on the values in Figure 2.15, the experimental and the estimated values of Young’s modulus are very close to one another and very comparable (%97).

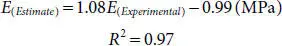
In this paper we evaluated the closeness of the estimated elastic wave velocities and elastic modulus of a rock sample via Gassmann - Greenberg - Castagna formula to those obtained from laboratory measurements at reservoir pressure.

Estimating the physical parameters of rock samples from Gassmann - Greenberg - Castagna equations at high pressures is farther from the real situation. At high pressure, velocity values are more differentiated from each other and the estimated values are observed to be very far from the experimental (laboratory) values. Although it appears that at higher pressures cracks or fractures get closed, in substituting the fluid, especially brine for supercritical carbon dioxide and water, elasticity values have very high variations, and this very strongly influences the estimated compression wave velocities. And finally, this effect can be seen on the shear wave derived from compression wave. But since the shear wave velocity in the fluid and gas behave similarly, the effect was observed less on this wave.

In the Gassmann assumptions it has been stated that pore fluid will not modify the elastic properties of the rocks. Thus, this theory predicts that shear modulus is not affected by the fluid saturation and will remain constant. In this study, the shear modulus didn’t remain constant during fluid saturation and during the transformation from gas-water saturation state to water saturation state; changes were detected to be around 2 percent. Because of this change in the shear modulus, it makes one hesitate to utilize the Gassmann theory to calculate the velocity. With the calculated and the experimental values of the shear modulus being variable, it can be concluded that Gassmann theory is not accurate for estimating the compressional wave velocity in a saturated state.

The research found that the bulk modulus values obtained from the laboratory experiments show a very weak compatibility with the values calculated using Gassmann formulas. One of the probable reasons for this could be an influence of the transformation of the rock skeleton by brine (salt water). The overall conclusion from these studies is that, for samples saturated in brine at low pressures, good agreement exists between bulk modulus values calculated from Gassmann formula and experimental values obtained in the laboratory. While at high pressures when the rock is very strongly influenced by pressure, this agreement is nonexistent. This change was about 9% at low pressures and at high pressures, these differences reached up to 23%. Therefore, one should contemplate before utilizing Gassmann equation.

Authors extended their appreciation to Petroleum Engineering Department, Curtin University of Technology, Australia that provided the authors the opportunity to utilize the laboratory core flooding system. Also, the authors thank and appreciate very much Prof. Vamegh Rasouli, Dr. Amin Nabipour, Dr. Mohammad Sarmadi and Dr. Mohsen Ghasemi for their help in conducting these experiments. Finally, the authors are very grateful and extend their deepest appreciation to the respected faculty of Petroleum Engineering and Geophysics departments, Curtin University of Technology that cooperated in the design, manufacturing and installation of the transducers.