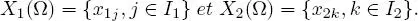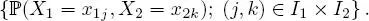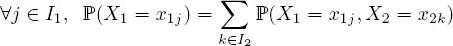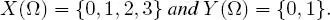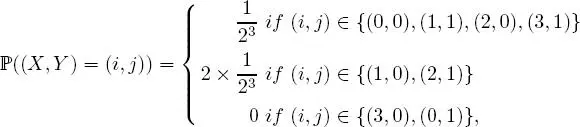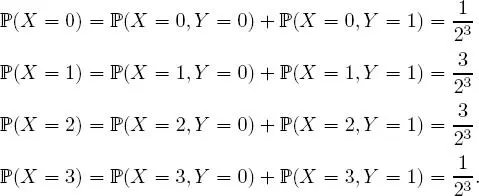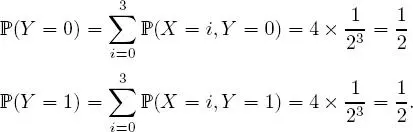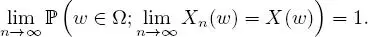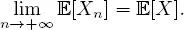The σ -algebra generated by X represents all the events that can be observed by drawing X . It represents the information revealed by X .
DEFINITION 1.14.– Let (Ω,  , ℙ) be a probability space .
, ℙ) be a probability space .
– Let X and Y be two random variables on (Ω, , ℙ) taking values in (E1, ε1) and (E2, ε2). Then, X and Y are said to be independent if the σ-algebras σ(X) and σ(Y) are independent.
– Any family (Xi)i∈I of random variables is independent if the σ-algebras σ(Xi) are independent.
– Let be a sub-σ-algebra of , and let X be a random variable. Then, X is said to be independent of if σ(X) is independent of or, in other words, and are independent.
PROPOSITION 1.8.– If X and Y are two integrable and independent random variables, then their product XY is integrable and 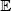 [ XY ] =
[ XY ] = 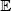 [ X ]
[ X ] 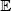 [ Y ].
[ Y ].
We will now more closely study random variables taking values in ℝ d, with d ≥ 2. This concept has already been defined in Definition 1.9. We will now look at the relations between the random vector and its coordinates. When d = 2, we then speak of a random couple.
PROPOSITION 1.9.– Let X be a real random vector on the probability space (Ω,  , ℙ), taking values in ℝ d . Then ,
, ℙ), taking values in ℝ d . Then ,
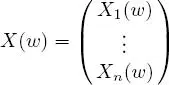
is such that for any i ∈ {1, ..., d }, X i is a real random variable .
DEFINITION 1.15.– A random vector is said to be discrete if each of its components, X i, is a discrete random variable .
DEFINITION 1.16.– Let  be a discrete random couple such that
be a discrete random couple such that
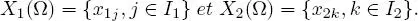
The conjoint distribution (or joint distribution or, simply, the distribution) of X is given by the family
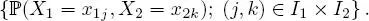
The marginal distributions of X are the distributions of X 1 and X 2 . These distributions may be derived from the conjoint distribution of X through:
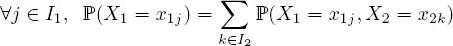
and

The concept of joint distributions and marginal distributions can naturally be extended to vectors with dimension larger than 2.
EXAMPLE 1.21.– A coin is tossed 3 times, and the result is noted. The universe of possible outcomes is Ω = { T, H } 3 . Let X denote the total number of tails obtained and Y denote the number of tails obtained at the first toss. Then ,
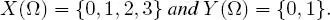
The couple ( X, Y ) is, therefore, a random vector (referred to here as a “random couple”), with joint distribution defined by
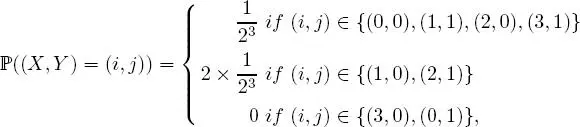
for any ( i, j ) X (Ω) × Y (Ω), which makes it possible to derive the distributions of X and Y (called the marginal distributions of the couple ( X, Y ) ):
Distribution of X:
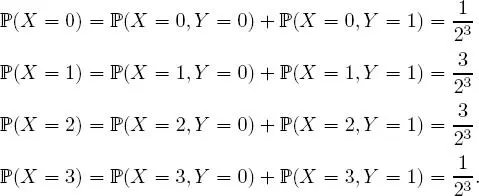
Distribution of Y :
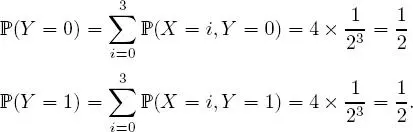

1.2.5. Convergence of sequences of random variables
To conclude this section on random variables, we will review some classic results of convergence for sequences of random variables. Throughout the rest of this book, the abbreviation r.v . signifies random variable .
DEFINITION 1.17.– Let ( X n) n≥1 and X be r.v.s defined on (Ω,  , ℙ).
, ℙ).
1 1) It is assumed that there exists p > 0 such that, for any n ≥ 0, [|Xn|p] < ∞, and [|X|p] < ∞. It is said that the sequence of random variables (Xn)n≥1 converges on the average of the order p or converges in Lp towards X, ifWe then write In the specific case where p = 2, we say there is a convergence in quadratic mean.
2 2) The sequence of r.v. (Xn)n≥1 is called almost surely (a.s.) convergent towards X, if
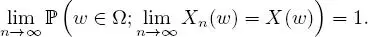
We then write
THEOREM 1.1 (Monotone convergence theorem).– Let ( X n) n≥1 be a sequence of positive and non-decreasing random variables and let X be an integrable random variable, all of these defined on the same probability space (Ω,  P) . If ( X n) converges almost surely to X, then
P) . If ( X n) converges almost surely to X, then
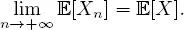
THEOREM 1.2 (Dominated convergence theorem).– Let ( X n) n≥1 be a sequence of random variables and let X be another random variable, all defined on the same probability space (Ω,  , ℙ) . If the sequence ( X n) converges to X a.s., and for any n ≥ 1, | X n|≤ Z, where Z is an integrable random variable, then and, in particular ,
, ℙ) . If the sequence ( X n) converges to X a.s., and for any n ≥ 1, | X n|≤ Z, where Z is an integrable random variable, then and, in particular ,
Читать дальше


 , ℙ) be a probability space .
, ℙ) be a probability space .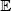 [ XY ] =
[ XY ] = 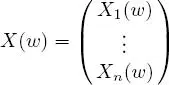
 be a discrete random couple such that
be a discrete random couple such that