EXAMPLE 1.23.– Let ( X n) n∈ℕ be a sequence of random variables and we consider, for any n ∈ ℕ,  n= σ ( X 0, X 1, ..., X n), the σ-algebra generated by { X 0, ..., X n} . The sequence (
n= σ ( X 0, X 1, ..., X n), the σ-algebra generated by { X 0, ..., X n} . The sequence (  n) n∈ℕ is, therefore, a filtration, called a natural filtration of ( X n) n∈ℕ or filtration generated by ( X n) n∈ℕ . This filtration represents the information revealed over time, by the observation of the drawings of the sequence X = ( X n) n∈ℕ.
n) n∈ℕ is, therefore, a filtration, called a natural filtration of ( X n) n∈ℕ or filtration generated by ( X n) n∈ℕ . This filtration represents the information revealed over time, by the observation of the drawings of the sequence X = ( X n) n∈ℕ.

DEFINITION 1.21.– Let (Ω,  , ℙ, (
, ℙ, (  n) n∈ℕ) be a filtered probability space, and let X = ( X n) n∈ℕ be a stochastic process .
n) n∈ℕ) be a filtered probability space, and let X = ( X n) n∈ℕ be a stochastic process .
– X is said to be adapted to the filtration (n)n∈ℕ (or again (n)n∈ℕ−adapted), if Xn is n-measurable for any n ∈ ℕ;
– X is said to be predictable with respect to the filtration (n)n∈ℕ (or again (n)n∈ℕ−predictable), if Xn is n−1-measurable for any n ∈ ℕ∗.
EXAMPLE 1.24.– A process is always adapted with respect to its natural filtration .

As its name indicates, for a predictable process, we know its value X nfrom the instant n − 1.
EXERCISE 1.1.– Let Ω = { a, b, c }.
1 1) Completely describe all the σ-algebras of Ω.
2 2) State which are the sub-σ-algebras of which.
EXERCISE 1.2.– Let Ω = { a, b, c, d }. Among the following sets, which are σ -algebras?
1 1)
2 2)
3 3)
4 4)
For those which are not σ -algebras, completely describe the σ -algebras they generate.
EXERCISE 1.3.– Let X be a random variable on (Ω,  ) and let
) and let 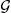 be a sub- σ -algebra of
be a sub- σ -algebra of  . Show that X is
. Show that X is 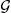 -measurable if and only if σ ( X ) ⊂
-measurable if and only if σ ( X ) ⊂ 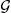 .
.
EXERCISE 1.4.– Let A ∈  and let
and let 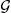 be a sub- σ -algebra of
be a sub- σ -algebra of  . Show that
. Show that 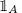 is
is 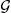 -measurable if and only if A ∈
-measurable if and only if A ∈ 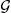 .
.
EXERCISE 1.5.– Let Ω = {P, F} × {P, F} and =  =
= 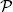 (Ω), corresponding to two successive coin tosses. Let
(Ω), corresponding to two successive coin tosses. Let
– X1 be the random variable number of T on the first toss;
– X2 be the number of T on the second toss;
– Y be the number of T obtained on the two tosses;
– and Z = 1 if the two tosses yielded an identical result; otherwise, it is 0.
1 1) Describe 1 = σ(X1) and 2 = σ(X2). Is X1 2-measurable?
2 2) Describe = σ(Y). Is Y 1-measurable? Is X1 -measurable?
3 3) Describe = σ(Z). Is Z 1-measurable, -measurable? Is X1 -measurable?
4 4) Give the inclusions between , 1, 2, and .
EXERCISE 1.6.– Let ( X n) n≥1be a sequence of independent random variables with the same Rademacher distribution with parameter 1 / 2:
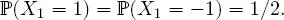
Let S 0= 0 and 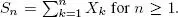 The process S = ( S n) n∈ℕis called the simple symmetric random walk on
The process S = ( S n) n∈ℕis called the simple symmetric random walk on  . It will be studied in detail in Chapter 3. We write X 0= 0. Show that the filtration generated by the sequence ( X n) n∈ℕis the same as that generated by the sequence ( S n) n∈ℕ.
. It will be studied in detail in Chapter 3. We write X 0= 0. Show that the filtration generated by the sequence ( X n) n∈ℕis the same as that generated by the sequence ( S n) n∈ℕ.
EXERCISE 1.7.– Consider the following game of chance. A player begins by choosing a number between 6 and 8 (inclusive), which we call the principal. The player then rolls 2 uncut, six-sided, non-rigged dice and sums the result. The wins are as follows:
– If the sum is 2 or 3, the player loses 1 DT (Tunisian dinar).
– If the sum is 11, the player wins 1 DT if the principal is 7; otherwise, they lose 1 DT.
– If the sum is 12, the player wins 1 DT if the principal is 6 or 8; otherwise, they lose 1 DT.
– Finally, in all other cases, nothing happens (no win, no loss).
1 1) Determine Ω, the universe of all outcomes of the experiment.
2 2) S is the random variable giving the sum of the two dice. Determine the distribution of S.
3 3) X7 is the random variable giving the player’s winnings (negative in the case of a loss) when the principal is 7. Determine the distribution of X7.
4 4) Calculate [X7] and (X7).
5 5) We consider X6 to be the winnings of the player when the principal is 6. Determine the distribution of X6 and then calculate [X6].
EXERCISE 1.8.– Let p ∈]0, 1[. We have one coin that leads to tails with the probability p . We toss this coin until we obtain tails for the second time. Let X be the number of heads obtained during this experiment.
1 1) Determine the distribution of X.
2 2) Justify the existence of the expectation of X.
3 3) Calculate [X].
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Читать дальше

 n= σ ( X 0, X 1, ..., X n), the σ-algebra generated by { X 0, ..., X n} . The sequence (
n= σ ( X 0, X 1, ..., X n), the σ-algebra generated by { X 0, ..., X n} . The sequence ( 
 be a sub- σ -algebra of
be a sub- σ -algebra of  is
is 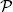 (Ω), corresponding to two successive coin tosses. Let
(Ω), corresponding to two successive coin tosses. Let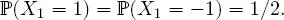
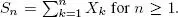 The process S = ( S n) n∈ℕis called the simple symmetric random walk on
The process S = ( S n) n∈ℕis called the simple symmetric random walk on  . It will be studied in detail in Chapter 3. We write X 0= 0. Show that the filtration generated by the sequence ( X n) n∈ℕis the same as that generated by the sequence ( S n) n∈ℕ.
. It will be studied in detail in Chapter 3. We write X 0= 0. Show that the filtration generated by the sequence ( X n) n∈ℕis the same as that generated by the sequence ( S n) n∈ℕ.










