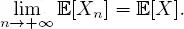
THEOREM 1.3 (Strong law of large numbers).– Let ( X n) n≥1 be a sequence of integrable, independent random variables from the same distribution. Then ,
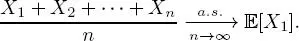
1.3. Stochastic processes
The main objective of this book is to study certain families of stochastic (or random) processes in discrete time. There are two ways of seeing such objects:
– as a sequence (Xn)n∈ℕ of real random variables;
– as a single random variable X taking values in the set of real sequences.
The index n represents time. Since n ∈ ℕ, we speak of processes in discrete time. In the rest of this book, unless indicated otherwise, we will only consider processes taking discrete real values. The notation E thus denotes a finite or countable subset of ℝ and ε = 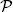 ( E ), the set of subsets of E .
( E ), the set of subsets of E .
DEFINITION 1.18.– A stochastic process is a sequence X = ( X n) n∈ℕ of random variables taking values in ( E , ε ) . The process X is then a random variable taking values in ( E ℕ, ε ⊗ℕ).
EXAMPLE 1.22.– A coin is tossed an infinite number of times. This experiment is modeled by Ω = { T, H } ℕ∗ . For n ∈ ℕ ∗, consider the mappings X n to Ω in ℝ defined by
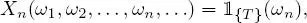
the number of tails at the nth toss. Therefore, X n, n ∈ ℕ ∗ are discrete, real random variables and the sequence X = ( X n) n∈ℕ is a stochastic process .
DEFINITION 1.19.– Let X = ( X n) n∈ℕ be a stochastic process. For all n ∈ ℕ, the distribution of the vector ( X 0, X 1 ,..., X n) is denoted by μ n . The probability distributions ( μ n) n∈ℕ are called finite-dimensional distributions or finite-dimensional marginal distributions of the process X = ( X n) n∈ℕ.
PROPOSITION 1.10.– Let X = ( X n) n∈ℕ be a stochastic process and let ( μ n) n∈ℕ be its finite-dimensional distributions. Then, for all n ∈ N∗ and ( A 0 ,..., A n−1) ∈ ε n, we have
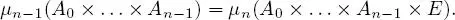
In other words, the restriction of the marginal distribution of the vector ( X 0 ,..., X n) to its first n coordinates is exactly the distribution of the vector ( X 0 ,..., X n−1).
PROOF.– This proof directly follows from the definition of the objects. We have
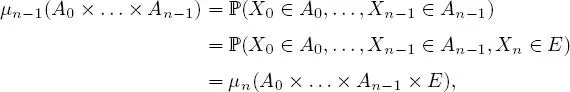
and hence, the desired equality.
□
Indeed, this property completely characterizes the distribution of the process X according to the following theorem.
THEOREM 1.4 (Kolmogorov).– The canonical space (Ω,  ) is defined in the following manner. Let Ω = E ℕ . The c oordinate mappings ( X n) n∈ℕ are defined by X n( ω ) = ω n for any ω = ( ω n) n∈ℕ∈ Ω and we write
) is defined in the following manner. Let Ω = E ℕ . The c oordinate mappings ( X n) n∈ℕ are defined by X n( ω ) = ω n for any ω = ( ω n) n∈ℕ∈ Ω and we write  = σ ( X n ,n ∈ ℕ) . Let ( μ n) n∈ℕ be a family of probability distributions such that
= σ ( X n ,n ∈ ℕ) . Let ( μ n) n∈ℕ be a family of probability distributions such that
1 1) for any n ∈ ℕ, μn is defined on (En+1, ε⊗(n+1)),
2 2) for any n ∈ ℕ∗ and (A0,..., An−1) ∈ εn, we have μn−1(A0 × ... × An−1) = μn(A0 × ... × An−1 × E).
Therefore, there exists a unique probability distribution μ over the canonical space (Ω,  ) such that the process X = ( X n) n∈ℕ for the coordinate mapping has the distribution μ and for the finite-dimensional distributions has the sequence ( μ n) n∈ℕ.
) such that the process X = ( X n) n∈ℕ for the coordinate mapping has the distribution μ and for the finite-dimensional distributions has the sequence ( μ n) n∈ℕ.
This result is very important for the theory of processes as it signifies that it is sufficient to specify (all) the finite-dimensional distributions and for them to be compatible with each other, to uniquely define a process distribution over the space of infinite random sequences. In practice, this makes it possible to justify the construction of processes (existence property) as well as showing that two processes have the same distribution (unicity property).
To study the random variables taking values in the set of sequences, we need new definitions for σ -algebras and measurability.
DEFINITION 1.20.– In a probability space (Ω,  , ℙ), a filtration is a sequence (
, ℙ), a filtration is a sequence (  n) n∈ℕ of sub-σ-algebras of
n) n∈ℕ of sub-σ-algebras of  such that, for any n ∈ ℕ,
such that, for any n ∈ ℕ,  n⊂
n⊂  n+1 . This is, thus, a non-decreasing sequence (for inclusion) of sub-σ-algebras of
n+1 . This is, thus, a non-decreasing sequence (for inclusion) of sub-σ-algebras of  .
.
When (  n) n∈ℕ is a filtration defined on the probability space (Ω,
n) n∈ℕ is a filtration defined on the probability space (Ω,  , ℙ), the quadruplet (Ω,
, ℙ), the quadruplet (Ω,  , ℙ, (
, ℙ, (  n) n∈ℕ) is said to be a filtered probability space .
n) n∈ℕ) is said to be a filtered probability space .
Читать дальше

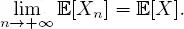
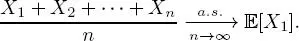
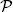 ( E ), the set of subsets of E .
( E ), the set of subsets of E .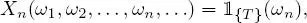
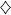
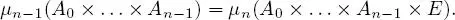
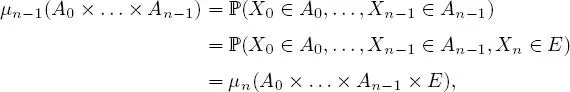
 ) is defined in the following manner. Let Ω = E ℕ . The c oordinate mappings ( X n) n∈ℕ are defined by X n( ω ) = ω n for any ω = ( ω n) n∈ℕ∈ Ω and we write
) is defined in the following manner. Let Ω = E ℕ . The c oordinate mappings ( X n) n∈ℕ are defined by X n( ω ) = ω n for any ω = ( ω n) n∈ℕ∈ Ω and we write 










