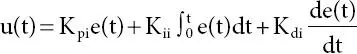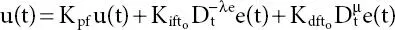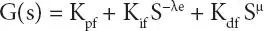where −1 is the rounding operation, c is the calculation step, and 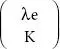 is the binomial coefficients defined as ϵ 0.
is the binomial coefficients defined as ϵ 0.
Integration and differential denoted by a uniform expression.
(2.3) 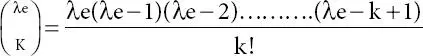
The fractional-order operator can be done by using the following equation [8]:
(2.4) 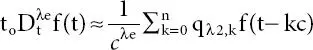
where 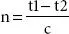
(2.5) 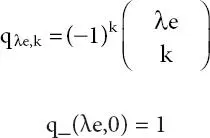
(2.6) 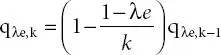
By ignoring the very old data, an approximate fractional-order approximation is obtained by
(2.7) 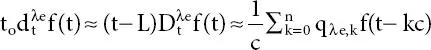
where 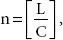 and L is the memory length.
and L is the memory length.
2.4.1.2 Fractional-Order PID Controller
The equation of the IPID controller is
(2.8) 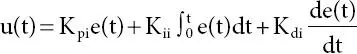
where K pi, K jjand K diand are the proportional, integral, and differential coefficient, respectively, where e(t) = y d(t) − y(t) is the system error, y d(t) is the reference input, y(t) is system response, and u(t) is controlled output [6, 9]. The FOPID controller is an extension of the conventional IPID controller with the integral and the differential orders as fractional one [7].
FOPID controller is represented as
(2.9) 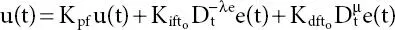
λe indicates integral order.
µ indicates the differential order.
K pf, K if, and K dfare fractional-order controller gains.
Laplace transfer function of the controller is given as
(2.10) 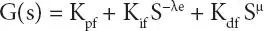
The FOPID has additionally more adjustable parameters, λ and µ, than IPID controller and have five control parameters ( Kpf , Kif , Kdf , λe, and μ) to find a better control performance [9]. For optimization, the GA has a possibility to come with five optimum parameter space to achieve best control performance.
GA is an adaptive empirical search algorithm depends on the mutative concepts of natural selection and genetics. It emphasizes the intellectual manipulation in finding solution to the optimization problems. Based on the historical information, GA searches for random variables through the best performance region of the search space. GA technique resembles the survival of the fittest principle proposed by Charles Darwin. In view of nature’s law, competition or struggle among the individuals results in the fittest predominating the inferior ones.
Alike chromosomes in DNA, the population in every generation has certain character strings impinged from the parent. In the search space each one of the individual signifies a point and has a feasible solution. The next stage through which the individuals undergo is the evolution process. Every individual in the population strives for the best position and mates. The fittest individual competes and yields offspring, whereas the inferior individuals will not proceed to the successive process. In every generation, the offspring thus produced from the fittest parent will be more suitable for the environment.
2.5.1 GA Optimization Methodology
GA optimization has for four major phases and requires a fitness function for optimization. The four steps are summarized as follows ( Figure 2.2):
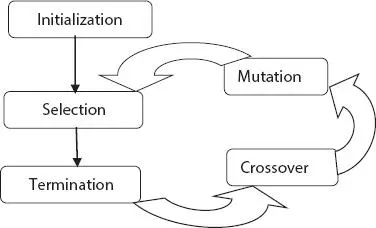
Figure 2.2 Phases in genetic algorithm.
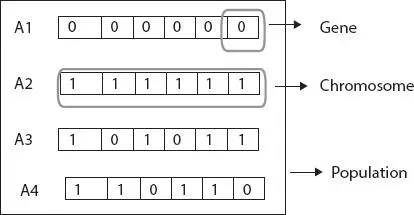
Figure 2.3 GA initialization process.
1 Initialization: population of chromosomes are initialized
2 Selection: reproduce chromosomes
3 Crossover: produce next generation of chromosomes
4 Mutation: random mutation of chromosomes in new generation
This is the initial phase in which a set of individuals are produced. Every individual is a solution to the problem and they are characterized by set of parameters called as genes. They are combined to form chromosome ( Figure 2.3).
Fitness function is the most crucial part of the algorithm. The capability of an individual entity to race with other entities is determined using fitness function. Fitness score is bestowed to every individual and the possibility for the selection of an individual for reproduction is entirely based on this score. It is the function that the algorithm optimizes. The word fitness is taken from evolutionary theory. Fitness is the word coined from evolutionary theory.
2.5.1.3 Evaluation and Selection
Population generation is followed by evaluation. It is the process in which the fitness level of the newly generated off springs is estimated using a fitness function. The inferior individuals are eradicated during selection and the best individual proceeds to the next generation.
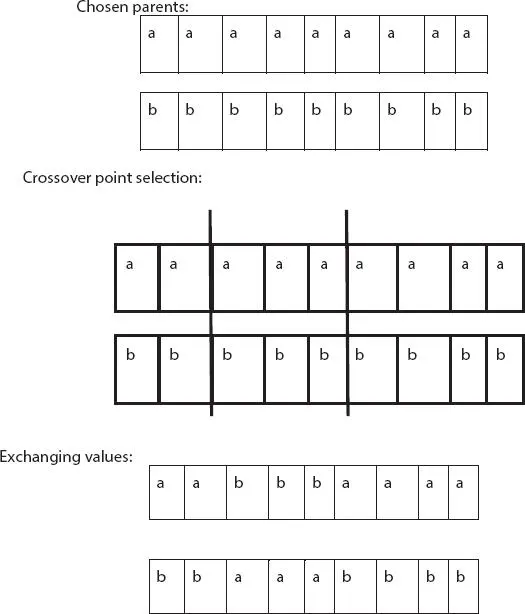
Figure 2.4 Crossover procedure.
The most important phase of GA is crossover. For every mating parent, a crossover point is randomly selected from the genes. Figure 2.4illustrates the crossover procedure. The procedure has three steps. First step is the selection of parents from the population. Crossover points are further selected. In Figure 2.4, the crossover points are shown as dotted lines. After the crossover points are selected, their values are exchanged to obtain a new offspring.
Читать дальше

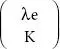 is the binomial coefficients defined as ϵ 0.
is the binomial coefficients defined as ϵ 0.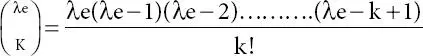
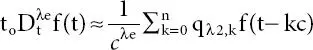
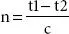
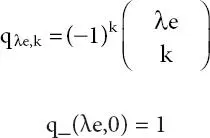
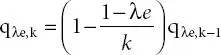
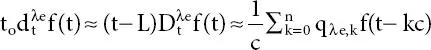
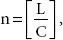 and L is the memory length.
and L is the memory length.