1.5 Stability Analysis Results
For small signal stability analysis, eigenvalue is calculated from system characteristic equation:
(1.54) 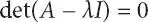
where unknown root λ is calculated (i.e., eigenvalue) with A and I as system matrix and identity matrix, respectively. For a system to be stable, all the real and/or real component of eigenvalues must be negative [15, 18–20].
State equation ( 1.53) and equation 8.3-45 of reference [15] are using nine and seven state variables, respectively. Hence, nine and seven eigenvalues will be obtained for six and three-phase generator, respectively. In six-phase generator, out of nine evaluated eigenvalues, three eigenvalues are complex conjugate pairs and the remaining are real. Evaluated eigenvalue of six-phase and three-phase generator is given in Tables 1.1and 1.2, respectively. Eigenvalue was evaluated by considering the same flux level in both three- and six-phase machine. This was ensured by considering the stator voltage of three-phase machine as twice of six-phase machine [27]. Hence, value of the terminal voltage for three-phase and six-phase machine was taken as 240 and 120 V, respectively. Results are given for both machine considering the same load at 50% of rated value, at power factor 0.85 (lagging). It is worthwhile to mention here that it is a difficult to establish a correlation of eigenvalue with machine parameter [15]. It has been considered by changing a machine parameter, keeping other at nominal value and noting the variation in eigenvalue [18].
Table 1.1 Eigenvalues of six-phase synchronous generator.
| Nomenclature |
Eigenvalues |
| Stator eigenvalue I |
−107.8 ± j104.7 |
| Stator eigenvalue II |
−19.2 ± j110.3 |
| Rotor eigenvalue |
−5.1 ± j38.2 |
| Real eigenvalue |
−9136.3, −703.5, −21.0 |
Table 1.2 Eigenvalues of three-phase synchronous generator.
| Nomenclature |
Eigenvalues |
| Stator eigenvalue |
−38.3 ± j103.2 |
| Rotor eigenvalue |
−27.9 ± j50.4 |
| Real eigenvalue |
−8719.7, −503.3, −10.7 |
In Equation ( 1.53), derivative component (i.e., with its elements with subscript p ) is indicated by coefficient matrix E , with remaining terms (i.e., subscript k ) of linearized machine equations are shown by the coefficient matrix F . Matrices E and F elements are defined in the Appendix.
1.5.1 Parametric Variation of Stator
During the analysis, it was assumed that the two sets of stator winding, say, abc and xyz , are identical. Hence, value of resistance and winding leakage inductance will be same (i.e., 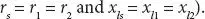 It may be noted that in figures of the following sections, dark and dash line indicate the real and imaginary component of eigenvalue, respectively.
It may be noted that in figures of the following sections, dark and dash line indicate the real and imaginary component of eigenvalue, respectively.
With increase in stator resistance, generator operation tends toward stability from both stator and rotor side due to higher magnitude of negative real component of eigenvalue, as shown in Figure 1.5afor three-phase generator and Figures 1.6aand bfor six-phase generator. Real eigenvalue I and II was found to be decreased as shown in Figures 1.5band cfor three-phase generator, and in Figures 1.6cand dfor six-phase generator. But a slight increase in real eigenvalue III of three-phase generator with no change was noted in six-phase generator as shown in Figures 1.5dand 1.6e, respectively.
With the increase in stator leakage reactance, a trend of eigenvalue variation was found to be reversed. On stator side, real component of eigenvalue was increased by 31.5% (shown in Figure 1.7a) for three-phase generator, and by 50% and 19.8% in stator eigenvalue I and II for six-phase generator, as shown in Figure 1.8a. However, a slight increase in real component of rotor eigenvalue for three-phase generator was noted, shifting the operation toward instability. But, in six-phase generator, increased magnitude of real component of rotor eigenvalue (shown in Figure 1.8b), signifying the tendency of stable operation. The remaining three eigenvalues remain negative with small variation as shown in Figures 1.7b– dand Figures 1.8c–efor three- and six-phase generator, respectively. It may be noted that the magnitude (with negative sign) real eigenvalues of six-phase generator remain higher (in magnitude); and hence, is more stable when compared with three-phase generator.
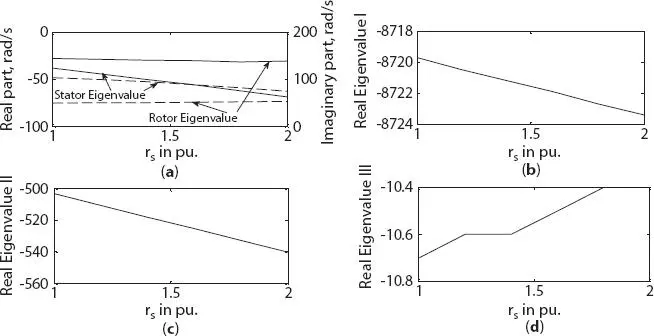
Figure 1.5 Variation in eigenvalue of three-phase synchronous machine with stator resistance change (a) stator and rotor eigenvalue, (b) real eigenvalue I, (c) real eigenvalue II, (d) real eigenvalue III.
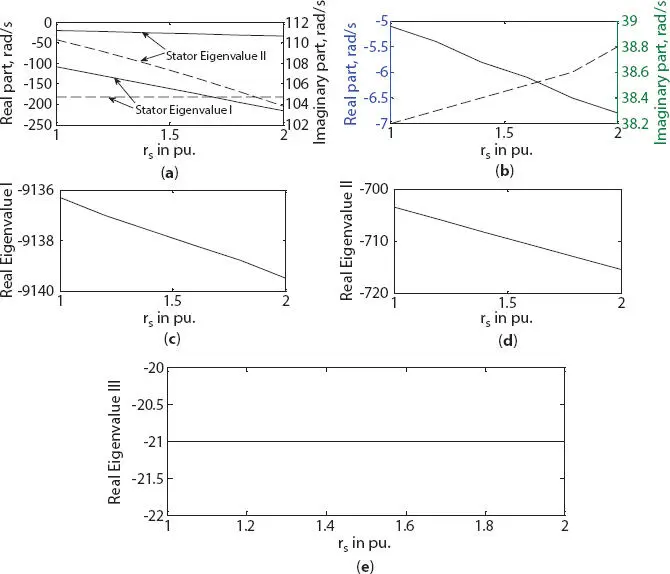
Figure 1.6 Variation in eigenvalue of six-phase synchronous machine with stator resistance change (a) stator eigenvalue I and II, (b) rotor eigenvalue, (c) real eigenvalue I, (d) real eigenvalue II, (e) real eigenvalue III.
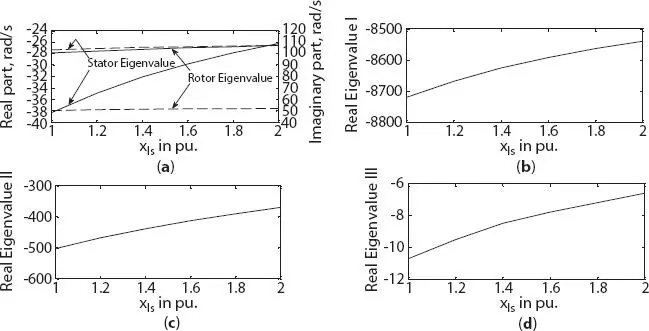
Figure 1.7 Variation in eigenvalue of three-phase synchronous machine with stator leakage reactance change (a) stator and rotor eigenvalue, (b) real eigenvalue I, (c) real eigenvalue II, (d) real eigenvalue III.
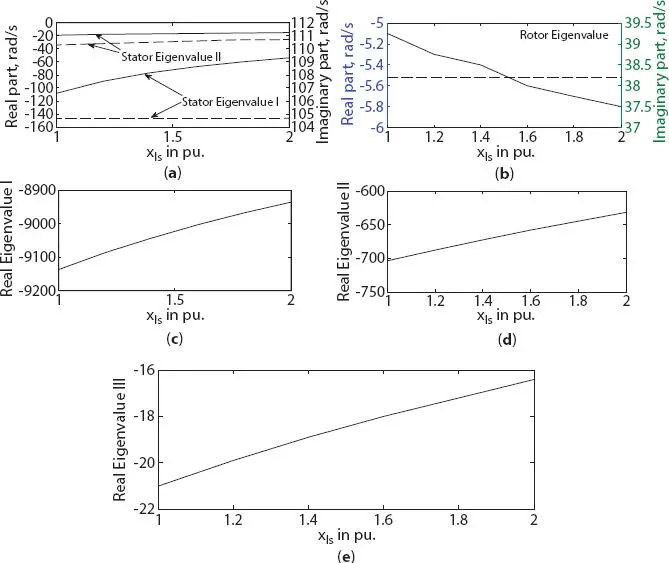
Figure 1.8 Variation in eigenvalue of six-phase synchronous machine with stator leakage reactance change (a) stator eigenvalue I and II, (b) rotor eigenvalue, (c) real eigenvalue I, (d) real eigenvalue II, (e) real eigenvalue III.
1.5.2 Parametric Variation of Field Circuit
In this section, the effect of variation in field circuit parameter (resistance rfr and leakage reactance xlfr ) is presented for both three- and six-phase generator. With the increase in field circuit resistance, variation in real component of stator eigenvalue was not observed in case of three-phase generator, as shown in Figure 1.9a. But, stator eigenvalue I was increased by 50%, showing the tendency of instability as shown in Figure 1.10b. But on rotor side, operation tends toward stability as shown in Figure 1.10b. A small increase in the value of real component of rotor eigenvalue was noted in three-phase generator, as shown in Figure 1.9a. Real eigenvalue I and III is decreased for three-phase generator as shown in Figures 1.9band d, respectively, with no variation in real eigenvalue II as shown Figure 1.9c. On the other hand, trend of variation in real component of eigenvalue was found to be different for six-phase generator. All the real eigenvalue I, II, and III was found to be decreasing (in magnitude with negative sign) as shown in Figures 1.10c, d, and e, respectively. It may be noted here that the larger variation was in the smallest real eigenvalue III with no or smaller change in other real eigenvalues. This is because, on rotor, field circuit has largest time constant giving rise to smallest eigenvalue III [15, 18].
Читать дальше

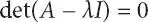
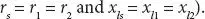 It may be noted that in figures of the following sections, dark and dash line indicate the real and imaginary component of eigenvalue, respectively.
It may be noted that in figures of the following sections, dark and dash line indicate the real and imaginary component of eigenvalue, respectively.














