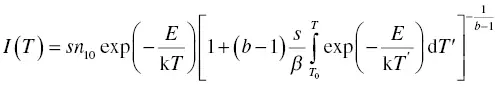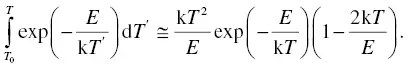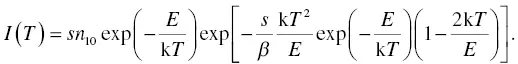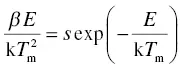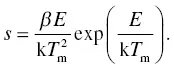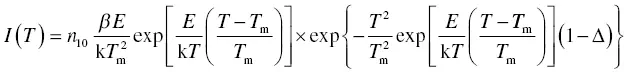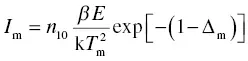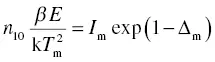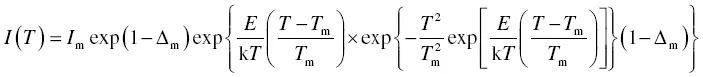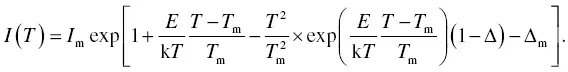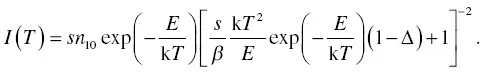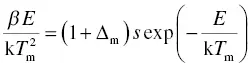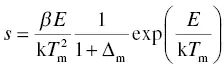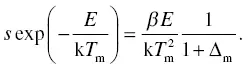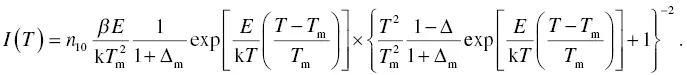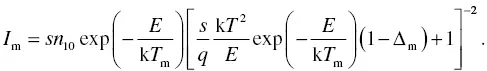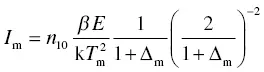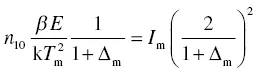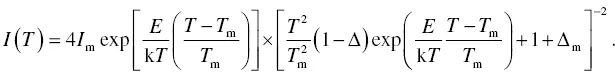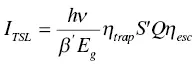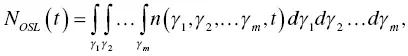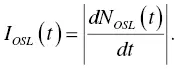In this equation, n 10means an electron density at T = T 0,which equals the concentration of electron trapping centers generated by ionizing radiation exposure. If we combine Equation (1.36)with Equation (1.37), we obtain
(1.38) 
Equation (1.38)represents a first‐order kinetics, and if the order is higher than 1, Equation (1.38)changes to
(1.39) 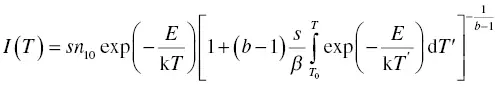
where b is an arbitrary order. Generally, if we can assume E ≫̸ kT and T 0= 0, then
(1.40) 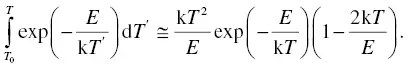
When we combine Equation (1.40)with Equation (1.38),
(1.41) 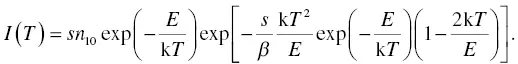
When we differentiate Equation (1.38)and assume it is equal to 0, it means there is a glow peak in the TSL glow curve. By using the glow peak temperature T m, we can obtain the relationship
(1.42) 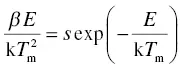
(1.43) 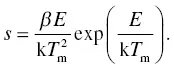
When we combine Equation (1.43)with Equation (1.41), we obtain the relationship
(1.44) 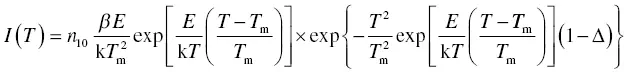
where Δ = 2k T / E . If we combine Equation (1.42)with Equation (1.41), we obtain a maximum TSL intensity of
(1.45) 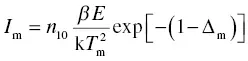
and the equation of
(1.46) 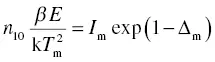
where Δ m= 2k T m/ E . If we combine Equation (1.46)with Equation (1.44), we obtain
(1.47) 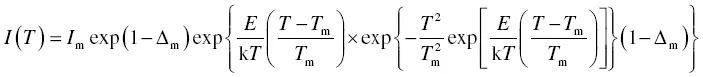
and
(1.48) 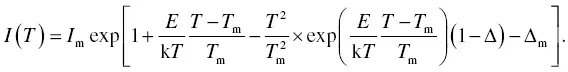
Equation (1.8)is a glow curve deconvolution function (GCD) of first‐order kinetics. In the case of second‐order kinetics (b = 2), Equation (1.39)becomes
(1.49) 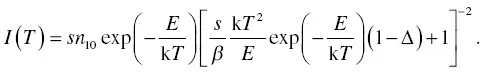
When I ( T ) shows the maximum, we can obtain equations such as
(1.50) 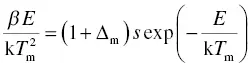
(1.51) 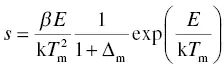
and
(1.52) 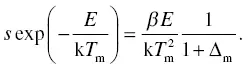
If we combine Equation (1.51)with Equation (1.49), the TSL intensity can be expressed as
(1.53) 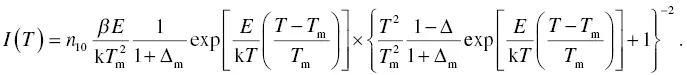
When the TSL intensity shows the maximum I m, Equation (1.49)can be rewritten as
(1.54) 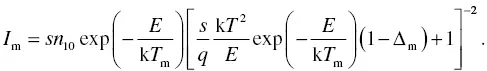
When we combine Equation (1.52)with Equation (1.54), the maximum intensity can be expressed as
(1.55) 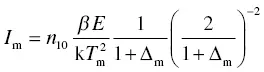
and relationship of
(1.56) 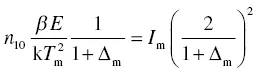
is deduced. Finally, if we combine Equation (1.56)with Equation (1.53), we obtain the equation on the second‐order kinetics of
(1.57) 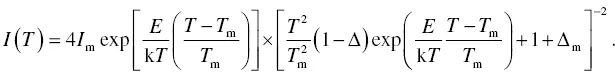
In addition to these standard analysis, analogical consideration of TSL efficiency with scintillation is considered as
(1.58) 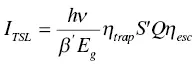
where η trap, S ′, and η escare the trap efficiency of carriers at trapping centers, carrier transfer efficiency to luminescence centers, and a probability that emitted photons are not absorbed in TSL material [81]. Other parameters have the same meaning with scintillation. Some analogical relation is proposed to TSL and OSL [82], and they essentially have the same physical meaning that scintillation and storage luminescence should be treated as one theory.
1.4.3 Analytical Description of OSL
Here, we introduce a basic analytical treatment of OSL, and explanations on practical applications and common materials are described in Chapter 8. The concentration of the metastable state occupied with an electron or hole ( N OSL( t )) can be expressed as
(1.59) 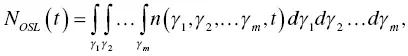
where γ 1, γ 2, … γ mmean the stability of the metastable state, that is they govern the probability per unit time in which the system will return to equilibrium, and n ( γ 1, γ 2, … γ m, t ) is a weighting function, or distribution, expressing the concentration of occupied states possessing the parameters γ 1, γ 2, … γ m, t . Then, OSL intensity I OSL( t ) is written as
(1.60) 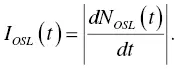
Читать дальше