Phosphors for Radiation Detectors

(1.19)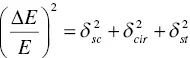

where δ sc, δ cir, and δ strepresent the intrinsic energy resolution, resolution due to circuit noise, and resolution expected by Poisson statistics, respectively. In pulse height spectrum, we observe Δ E / E directly, and we can estimate δ stby the number of scintillation photons and the quantum efficiency of the photodetector. The circuit noise δ circan be directly estimated by the injection of a test pulse into the electrical circuit. Thus, we can calculate δ scby the subtraction of δ stand δ cirfrom Δ E / E . Under most experimental conditions, estimation must consider a contribution not only by the scintillator but also by the photodetector, and the simplest measurement can be possible by Si‐PD because it has no internal gain. When we measured and calculate the intrinsic energy resolution, that at 662 keV of Tl‐doped NaI was 2.5% [64], Tl‐doped CsI was 5% [65], Ce‐doped LaBr 3was 2.2% [66], Ce‐doped LuAG was 4.5% [66], and Ce‐doped LSO was 7.7% [66]. At present, the remaining problem is whether the intrinsic energy resolution we are observing is a fundamental limit or not, and whether the intrinsic energy resolution is the physical property of each material or not (detector property). The detailed explanations on energy resolution and intrinsic energy resolution are described in Chapter 12.

In an ideal scintillation detector, energy response (signal output intensity vs. incident radiation energy) should have a simple proportional relationship; however, the energy responses of actual detectors are not simple. The main reason is a non‐proportional energy response of scintillators. Figure 1.6(top) shows a non‐proportional response plot, which shows a relationship between relative light output (pulse height) per unit energy and irradiated γ‐ray energy. Although Eu‐doped SrI 2, Ce‐doped CLYC, and Pr‐doped LuAG show a relatively flat response against γ‐ray energy, BaF 2, Ce‐doped GAGG, and Tl‐doped NaI exhibit a large fluctuation against γ‐ray energy. When we use the latter three types of scintillators as actual detectors, we must apply the gain correction function to measure the energy accurately. The main origin of the non‐proportional response is considered as related to the K‐edge of the main element of scintillator. This was first pointed out in Ce‐doped GSO [67]. Now, we understand that the flat response against γ‐ray energy is required to achieve high energy resolution. In practical scintillation detectors, we generally use a function between γ‐ray energy and pulse height, as shown in the bottom of Figure 1.6. In a simple case, we fit the relationship by a linear function with the least squares method, and the bottom panel in the bottom of Figure 1.6shows the residual from linear fitting at each energy. After we prepare such a fitting function, we can convert pulse height channel to energy of ionizing radiation focused on each measurement. Although these two figures have the same physical meaning, people in basic science prefer a non‐proportionality plot, and those using the actual detector prefer a linearity plot.

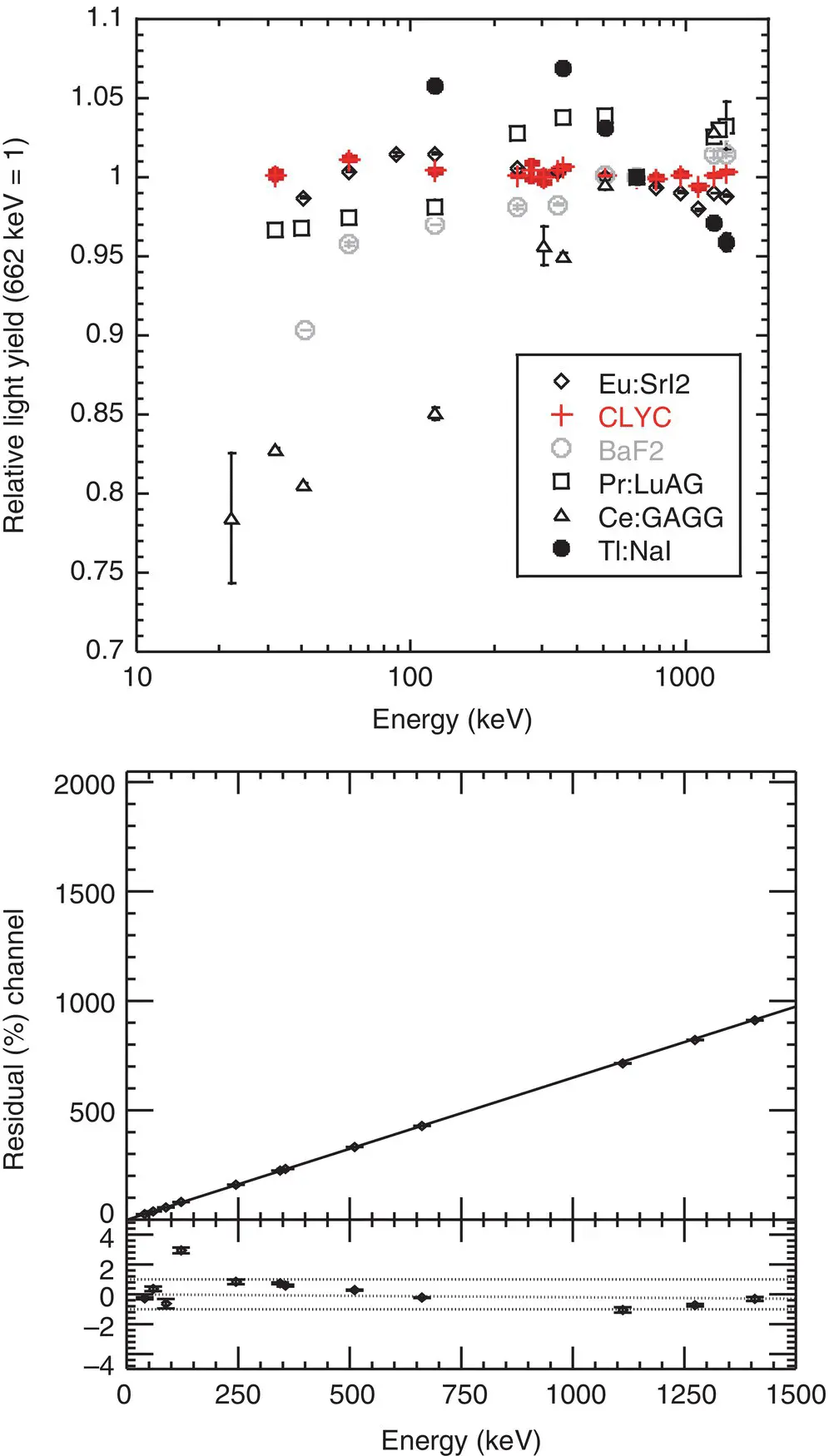
Figure 1.6 (Top) Relationship between the scintillation decay time (ns) and emission wavelength (nm) and (bottom) relationship between γ ‐ray energy and photoabsorption peak channel.

Timing properties are also important for scintillation detectors, and depend on the rise and decay times of scintillators and photodetectors. Generally, we analyze the decay time profile by the sum of multi exponential functions, which can be understood as a typical rate equation. Here, we assume radiative and non‐radiative rate constants of k rand k nr, respectively. N ( t ) is the number of excited states, and it shows a relaxation with a rate of –Δ N rduring a very short time of Δ t . This can be formulated as

(1.20)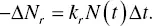

The number of the decrease of excited states –Δ N nris expressed as

(1.21)

Totally, the decrease of the excited states –Δ N is a sum of Equations (1.20)and (1.21), and it can be expressed as

(1.22)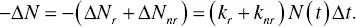

Thus, we can obtain

(1.23)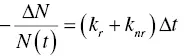

We can solve this differential equation as

(1.24)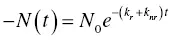

where N 0means the number of luminescence centers at t = 0. If we define k r+ k nr= 1/ τ , we can obtain a typical decay time function for the analysis. Unlike the case of the decay time, the common confirmed analysis method for the rise time has not yet been constructed. One of the problems with the rise time is that it is too fast for typical photodetectors and irradiation sources to observe. Except for scintillators with very slow rise times, the typical rise time is in the order of ~ps, and it is technically difficult to detect such a fast phenomenon.

To date, unlike the situation of scintillation light yield, no widely accepted and confirmed model has been constructed. We apply a common model of PL to understand the scintillation phenomenon. The common relationship between scintillation decay time is expressed as

(1.25)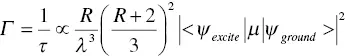

where Γ means the radiative decay rate, τ is the decay time, R is the refractive index, λ is the emission wavelength, ψ exciteis the wave function of excited state, ψ exciteis the wave function of ground state, and μ is the electric dipole operator between the initial lowest energy of excited state and the final state of the configuration, respectively [68]. Based on this relationship, we understand that scintillators with shorter emission wavelengths show smaller decay times if we compare them with scintillators possessing the same emission mechanisms (e.g., comparison among d‐f transitions). Figure 1.7shows the relationship between the scintillation decay time and emission wavelength of some common materials. In this plot, we use Ce 3+, Pr 3+, and Nd 3+doped samples, and the emission mechanism of all the samples is 5d‐4 transition. A clear proportional relationship based on Equation (1.25)is clearly observed. Typically, emission wavelength due to d‐f transitions of Ce 3+, Pr 3+, and Nd 3+appear in the visible, ultraviolet, and vacuum ultra violet wavelengths, respectively. If we plot the same relationship on 4f‐4f transitions of rare earth ions, a similar relation will be obtained, but it is technically difficult to measure the scintillation decay time of near infrared emission, which is the typical emission wavelength of 4f‐4f transition of rare earth ions.