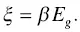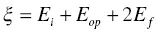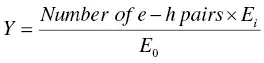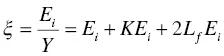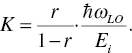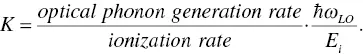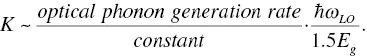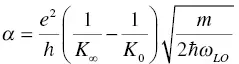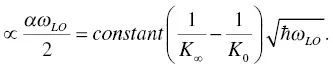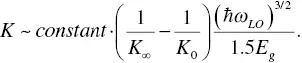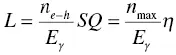Phosphors for Radiation Detectors

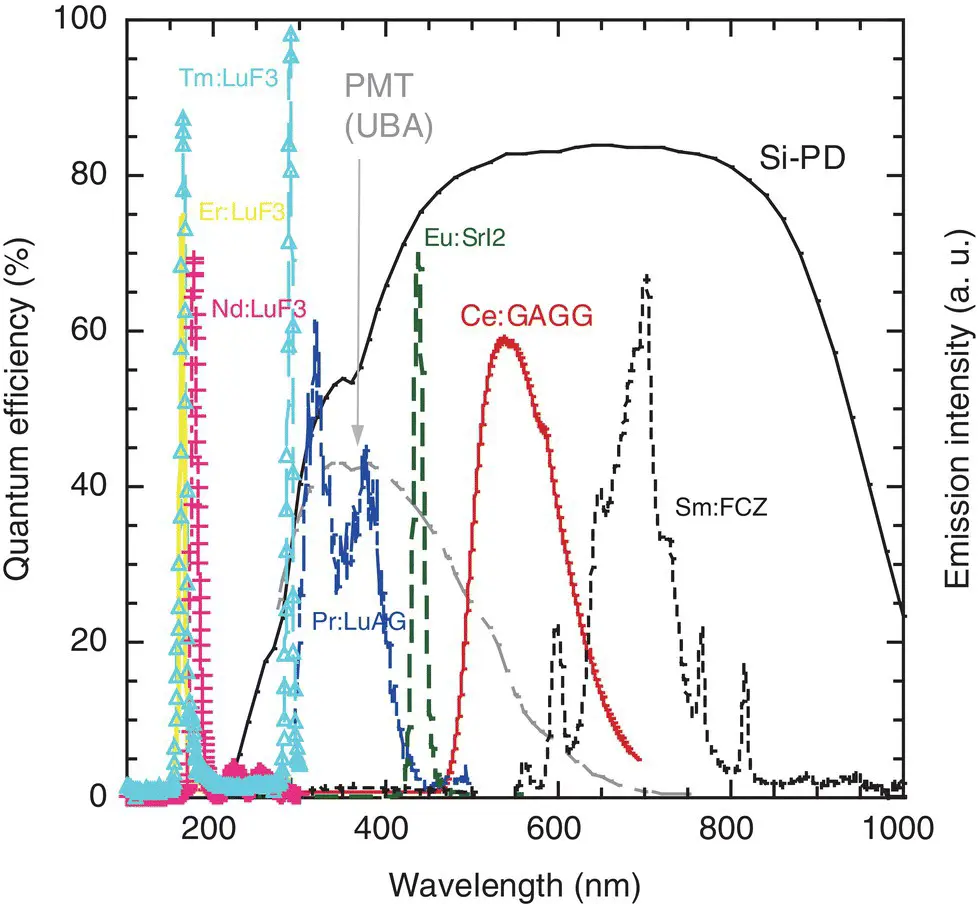
Figure 1.5 Emission spectra of scintillators under X‐ray irradiation and typical quantum efficiencies of Si‐PD and PMT.

In addition to the emission wavelength, light yield is the most important property for scintillators because it directly determines the signal to noise ratio (S/N) in all types of scintillation detectors. The scintillation light yield generally uses the unit of ph/MeV, which means a number of emitted scintillation photons with 1 MeV absorption of ionizing radiation. Typically, we measure it by X‐ and γ‐ray irradiation. It must be noted that the light yields of one scintillator are different by species of irradiated ionizing radiation. If we irradiate 5.5 MeV α‐ray from 241Am and 662 keV γ‐ray from 137Cs to one sample, the observed light yields are different. The relative ratio of light yields under α‐ray and γ(β)‐ray irradiation is known as the α/γ‐ (α/β‐) ratio. Although we do not have a universal theory for this ratio, empirically, the ratio of halide scintillators is close to 1, while that of oxide scintillators is ~0.2. In some fields of radiation physics and chemistry, the difference of energy conversion efficiency of different ionizing radiation species is recognized as the linear energy transfer (LET) effect.

Here, we will introduce the common explanation on the scintillation light yield. The semi‐empirical approach was made in 1980 by Robbins [56] based on semiconductor physics. In the semiconductor radiation detector, empirical relation of ξ (average energy consumed per electron–hole pair) and E g(band‐gap energy) are connected by a parameter β as

(1.2)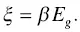

In this approach, to consider ξ , the energy of electron–hole pairs, falls below the threshold energy for impact ionization:

(1.3)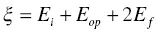

where E i, E op, and E frepresent the threshold energy for impact ionization, energy emitted as optical phonons, and average residual energy of electron–hole pairs, respectively. Throughout this discussion, the unit of ξ (energy) is eV. Here, we consider the branching ratio of optical phonon emission with the probability of r and the impact ionization with (1‐ r ) under the initial absorbed energy of E 0. If the energy after some processes, such as impact ionization and phonon emission, remains at > E i, the impact ionization (excitation process) continues. In the ideal case, the limiting efficiency ( Y ) of the production of electron–hole pairs is

(1.4)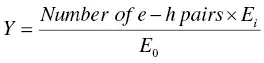

and by using this relation, the average energy per electron–hole pair is re‐written as

(1.5)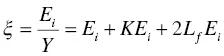

where L f= E f/ E iand K means the ratio of rate of optical phonons rate of energy loss by ionization, expressed as

(1.6)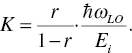

In this equation, ℏω LOmeans the energy of the longitudinal optical phonon. If we assume this energy and the optical phonon energy is constant, K can be expressed as

(1.7)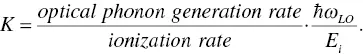

Here, we assume special conditions of: (i) Ionization rate is constant for carrier energy; and (ii) E i= 1.5 E g, and according to the avalanche multiplication data of Si, then K can be approximated to

(1.8)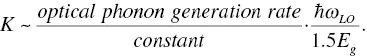

In order to proceed with the calculation, we assume a polaron model where a polaron accompanies α /2 phonons, then α can be expressed as

(1.9)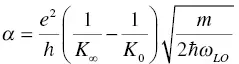

where K ∞and K 0are static and high‐frequency dielectric constants, respectively. Under this condition, the optical phonon generation rate is proportional to

(1.10)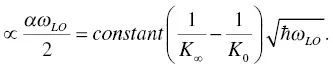

Thus, K can be expressed as

(1.11)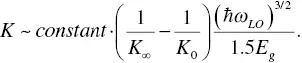

By using these equations, we can estimate the scintillation emission efficiency semi‐empirically. Following this first approach, the model was modified for actual use in daily experiments. In 1994 [57], the scintillation light output L per unit energy was expressed as

(1.12)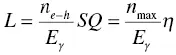

where n e‐his the number of electron–hole pairs under γ‐ray with energy of E γirradiation, n maxis the number of electron hole pairs which would be generated if there were no losses to optical phonons, S stands for transfer efficiency from the host to luminescence centers, Q is luminescence quantum efficiency at localized luminescence centers, and η is total scintillation efficiency.

Here, we will proceed with further consideration that this assumption is E i= 1.5 E g. In the Robbins approach [56], the average energy used to produce one electron–hole pair under assumption of no optical phonon loss is ξ min= 2.3 E g, and in this case, n max= 10 6 E γ/2.3 E gwhere we use the energy unit of eV. Because n e‐h= 10 6 E γ/2.3 ξ and n max= 10 6 E γ/ ξ min, we can deduce that β s= ξ min/ ξ . In Equation (1.5), if we assume K = 0, we have ξ min= 1.5 E g(1 + 2 L f), and if we use the relation of ξ min= 2.3 E g, L f= 0.27. If we assume L fdoes not depend on K , we can use L f= 0.27 in Equation (1.5), and the average energy consumed per electron–hole pair can be expressed as ξ = E g(2.3 + 1.5 K ). Under this condition, the parameter β is approximated to