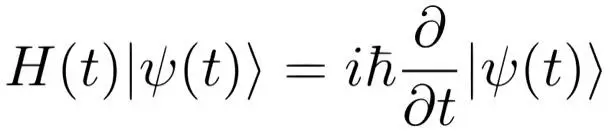Paul J. van Leeuwen - Quantum Physics is NOT Weird

To be frank with you, when I started to try to understand the meaning of the double slit experiment with electrons I was confused too and called the outcome of the observed double slit experiment proof of particle behavior. This will turn out to be defensible in a certain way. We will see that the fact that the quantum wave passes through only one of the slits informs us that the probability that the particle was at some time in that slit, is 100%. A probability of 100% is in fact the same as saying that the particle was in the slit. But was it there in a physical way?

Until 1925 a unified solid mathematically formal basis of quantum physics was missing. Quantum physics had become a haphazard collection of – albeit intelligent – assumptions. So, in that year, Werner Heisenberg(1901-1976) not being content with this state of affairs, came up with a new mathematical tool for quantum mechanics, matrix mathematics. The location and intensity of the spectral lines of glowing hydrogen gas could be calculated precisely with his matrix mechanics. However, Heisenberg’s matrix mathematics was for most physicists a rather exotic branch of mathematics. Moreover, it provided no insight, as classic mechanics does, into the underlying mechanisms, it produced only discrete outcomes.

Surprisingly, in matrix mathematics the outcome of A x B is not equal to B x A. This corresponds very well with the phenomenon that the outcome of a quantum experiment depends on the order of your measurements. Anyway, the results of Heisenberg’s matrix mechanics were in very good accordance with the observed discrete values for the wavelengths in the hydrogen spectrum. This made matrix mechanics a very valuable tool for doing quantum physics calculations. But it delivered no useful suggestion whatsoever for a possible interpretation of quantum phenomena.

Progress in quantum physics was now well underway. One year later, in 1926, Erwin Schrödinger(1887-1961) published what is now known as the Schrödinger equation for quantum mechanics. We will pay more attention to his mathematics later. Shortly thereafter, in 1927, Heisenberg formulated his famous uncertainty principle. It says that there is an inverse relationship between the accuracies with which the momentum p (mass times velocity) and the position of a particle can be measured. There is a fundamental limit to the accuracy of your measurements that is not dependent on your measuring instruments. In 1929, Heisenberg and Wolfgang Pauli published the foundations of relativistic quantum mechanics. With these new mathematical tools, a solid theoretical basis was finally laid. Physics now even possessed two different mathematical tools to make quantum mechanical predictions.

For the sake of completeness, you’ll find below the Schrödinger equation for a single particle. The explanation of the meaning of the symbols is beyond the scope of this book and is by no means necessary for understanding the conclusions that we will draw from the observations and experiments in quantum physics.

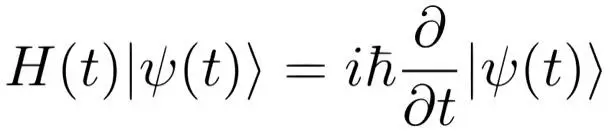
Schrödinger sought, and found, his famous equation because he was already proficient in wave mechanics and because he realized that the electron wave model of De Broglie for a hydrogen atom with one single electron could not explain why that hydrogen-atom was not flat as a dime. It should be something like a tiny sphere. Schrödinger’s discovery came in a flash of inspiration. It was not the result of a patient mathematical analysis. He was racking his brains searching intensely for a mathematical equation describing a 3-dimensional standing electron wave extending in three directions around the nucleus of the atom. But the solution was revealed to him in a flash of insight while spending a relaxed holiday with an extramarital love.

For the purpose of this book, you don’t have to understand the Schrödinger equation, let alone apply it. However, it is important to understand that the wave function calculated with the Schrödinger equation represents the wavelike development over time of the location, the momentum, and the energy of the particle, but not so that we can know those properties in an exact way. This has to do with the fact that a wave has no distinct location. It spreads out in time and space. You cannot even say that these properties exist, in a material sense, before measurement.

To avoid confusion of terms, I will define here the following strongly related, but different in meaning, quantum wave concepts as they are used in this book:

Quantum wave or state wave: The non-material wave behaving conform the solution of the Schrödinger equation.

Wave function or state function: The mathematical expression that is the solution of the Schrödinger equation describing the quantum wave.

The uncertainty principle, or uncertainty relation, of Heisenberg is shown below.

Δp.Δx ≥ h/4π

The uncertainty in the location x is Δx, the uncertainty in the momentum p is Δp. Their multiplied value has an unsurpassable lower limit specified by Planck’s constant h divided by 4π.

This uncertainty relation can be made somewhat plausible by considering the diffraction of light waves going through either a smaller or wider hole or slit. Figure 5.7 shows what happens when we shine a beam of light, photons, through a wide and through a small opening. With a wide opening, most photons will continue in an almost straight line, the light waves passing through are only slightly disturbed by the edges of the opening. When you shine a beam of light at the opening, the result will be a rather sharply defined spot of light.

A small opening – small when compared with the wavelength – will act as a point wave source (Huygens) from where the light waves will extend spherical. The result is then a fuzzy spot with decreasing intensity towards the edges like the bold curve in figure 5.6.

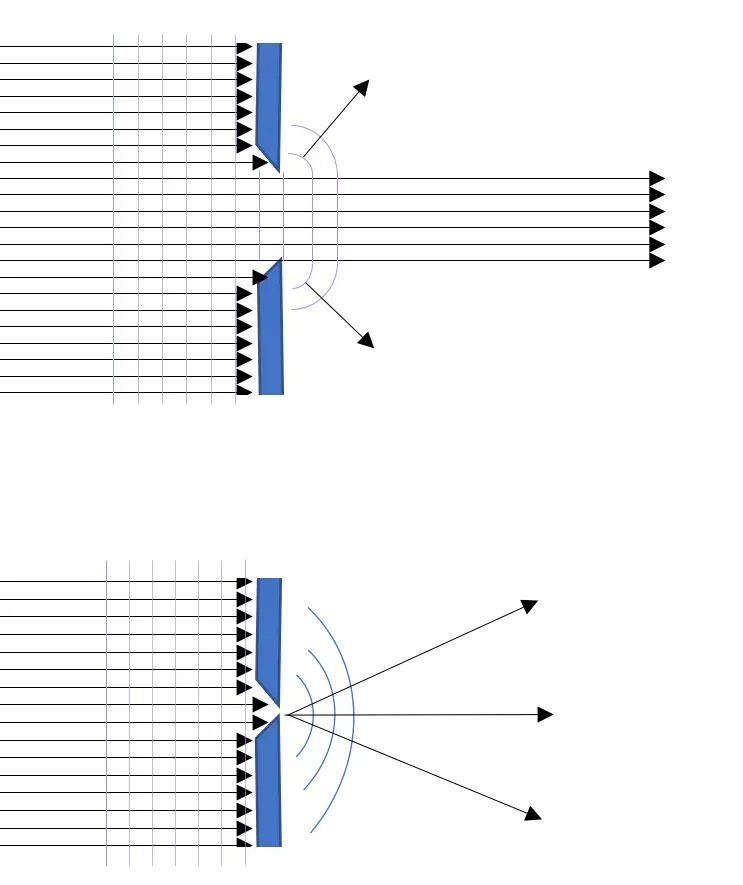
Figure 5.7: Wide opening, less diffraction. Small opening, strong diffraction

When we would observe the projected light pattern a little bit more closely, we would see an interference pattern, the so-called Fraunhofer diffraction [ 5 ].

Diffraction is a known phenomenon that plays an important role with photo cameras. The smaller the aperture – the diameter of the diaphragm – the sharper objects located in a wide range of distances relative to the camera will be displayed. But when the camera diaphragm is made too small, the image will blur again by wave diffraction. This is not a camera defect but the result of the wave behavior of light and, as you now understand, connected to Heisenberg’s uncertainty principle.

What is now the message of this? The answer is that as soon as you try to define the path of the photon using a small aperture, the photon will scatter in all directions. The reason for this scattering of the photon is that it ‘is’ (also) a wave that is influenced in its course by the edges of the opening. With a large opening, that influence is smaller.

You must have noticed the duality in the above descriptions. The photon behaving both as a wave and as a particle. Sometimes, that kind of language is almost unavoidable in talking about quantum physics. However, keep this in mind: the wave is NOT the particle, as we’ll see.

Heisenberg diffraction experiment: Create a pinpoint hole with a fine needle in an opaque sheet of paper or carton. Then make the room as dark as possible. Thereafter shine with a laser on the pinpoint hole. A laser projects coherent light, which means synchronous parallel traveling wave fronts. Observe the projection on a nearby wall of the laser light that passed the pinhole. What should you observe? What do you observe?