Paul J. van Leeuwen - Quantum Physics is NOT Weird

Figure 4.8 gives a wavelength = 122 nm for that. With that you can calculate the transition energy ΔE = (6.626 × 10−34 x 3 x 108)/(122 x 10-9) = 0.163 x 10-17 J. Now calculate the transition energy ΔE3-2from orbit 3 to orbit 2 with = 656 nm. Finally calculate the direct transition energy from orbit 3 to orbit 1 ΔE3-1with = 103 nm. Then the following should be true:

ΔE 3-1= ΔE 3-2+ ΔE 2-1

You can demonstrate in the same way:

ΔE 4-1= ΔE 4-2+ ΔE 2-1= ΔE 4-3+ ΔE 3-1 =ΔE 4-3+ ΔE 3-2+ ΔE 2-1

So, it seems indeed be that only certain fixed energy levels for electrons, orbiting the hydrogen nucleus, were allowed. But the fundamental reason for that restriction of nature remained at that time a mystery for Bohr and his contemporaries. It was compelling that the measured wavelengths of the spectral lines exactly matched the differences between a limited set of distinct energy levels, but that match was not convincing enough for scientific acceptance. More evidence, especially an acceptable explanation for those permitted energy levels, was required.

A surprising explanation was proposed in 1923. This was the result of the daring and inspired insight of a French prince. But before going into that, we must pay some attention to standing waves in strings.

A vibrating string has only very specific ways in which a standing wave can arise and continue. The condition is that an integer number of half wavelengths fits exactly on the length of the string. Which means ½λ, 1λ, 1½λ, 2λ, 2½λ, etc. You get the lowest vibration – the tonic – if exactly ½λ fits on the string. With 1λ fitting on the string you get the 1st harmonic, with 1½λ fitting on the string you get the 2nd harmonic, and so on. This means that there will always be a lowest vibration for any given string, to evoke a lower tone is impossible. The possible vibrations are clearly ‘quantized’ and have a lowest boundary. This phenomenon inspired prince Louis Victor de Broglie to a rather daring idea.

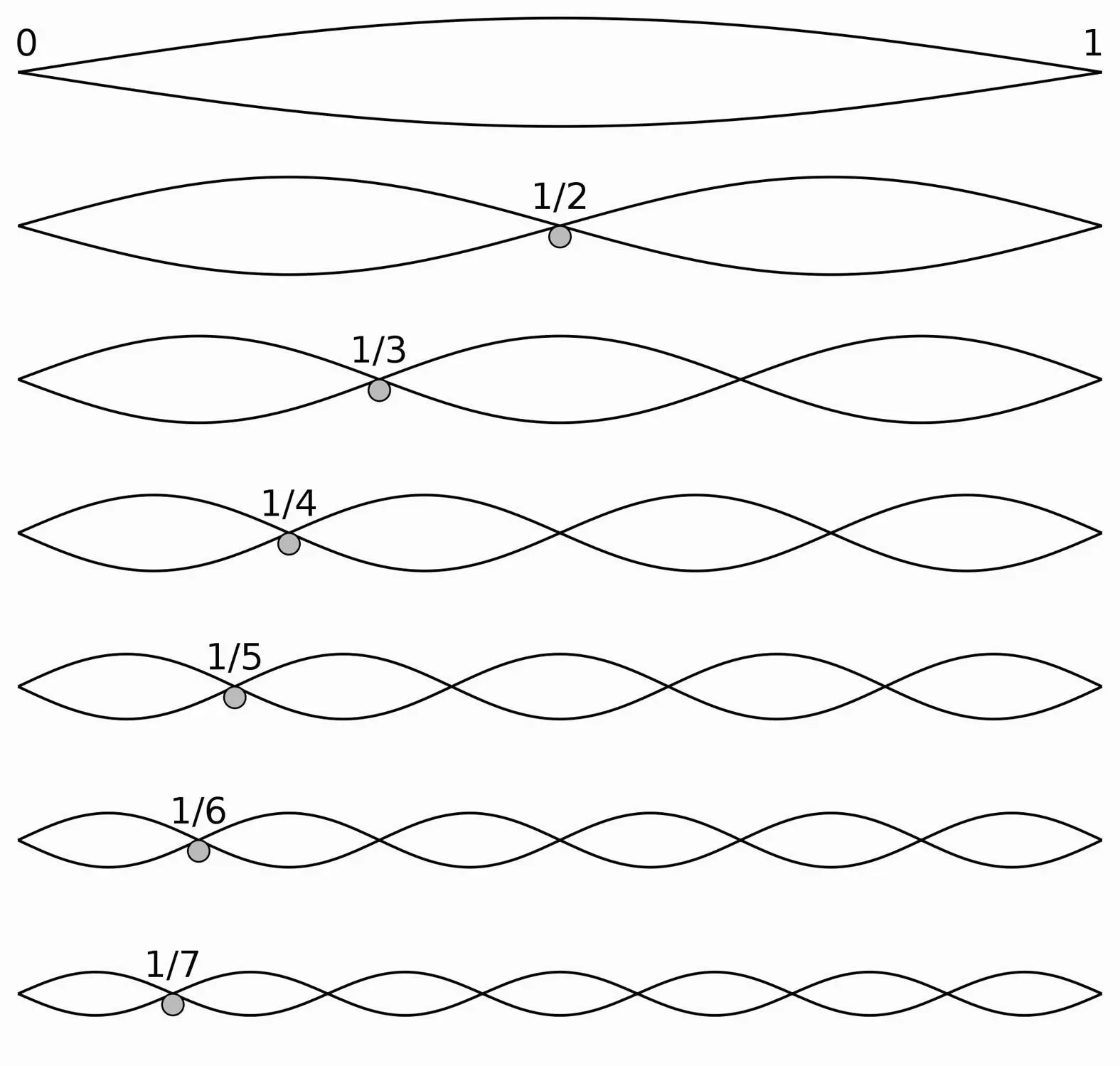
Figure 4.9: Seven harmonically vibrating modes of a string. From tonic to 6 thharmonic.

Source: Wikimedia Commons.

Thinking about Bohr's still enigmatic atomic model and familiar with Einstein's photons – EM-waves behaving as particles – Louis Victor de Broglie (1892-1987) connected in 1923 the dots and supposed that if a wave could be a particle, the other way around might also be true. Could it be possible that those enigmatic Bohr electron orbits were standing electron waves?

If electrons behaved like standing waves, then their waves would only fit on their orbits around the nucleus in certain ways, just like standing waves on vibrating strings. When the electron wavelength fitted exactly on circular orbits of 1 λ, 2 λ, 3 λ, etc. this would result in standing electron waves.

De Broglie knew very well that a moving particle, such as an electron, has a certain momentum p = m.v,where m.v denotes mass times speed. Combining this with the Planck formula for the energy of a light particle and Einstein’s energy-mass equivalence, he proposed that this determined the associated wavelength of a moving electron.

It was already confirmed by the photoelectric effect [ 2 1 ]that a photon has an associated momentum. Combining E = h.f, E = m.c2and p = m.vDe Broglie arrived at a simple formula for the wavelength of an electron: λ = h/(mv). This tells that the greater the speed vis, the shorter the associated electron wavelength λwill be. When jumping to a higher orbit the speed of the electron will be slowed down and its wavelength will therefore grow accordingly.

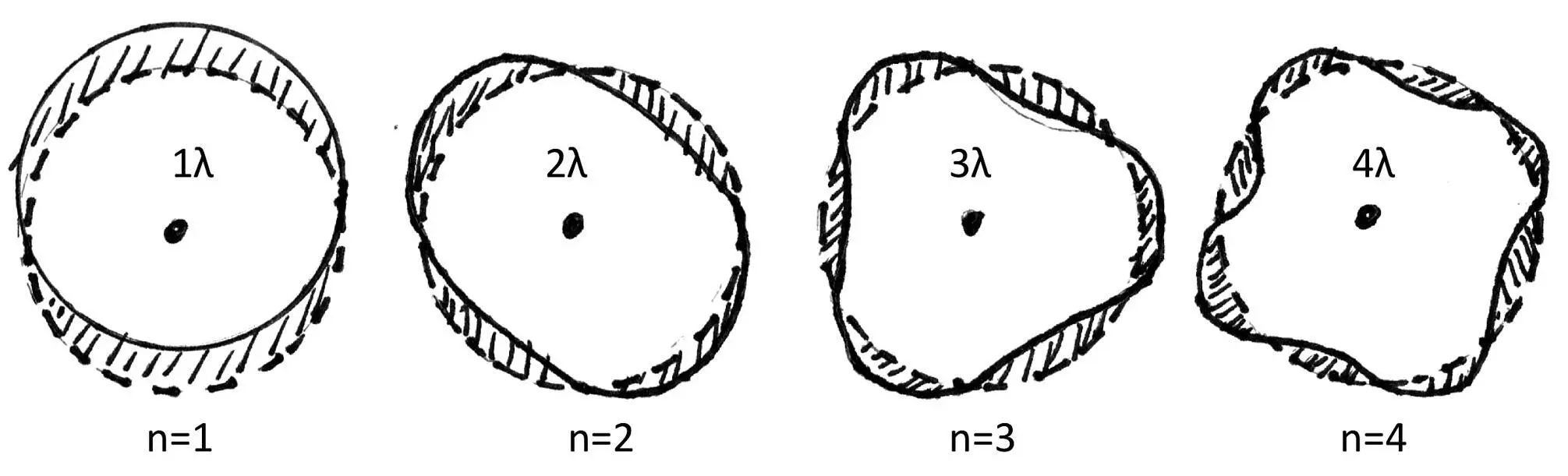
Figure 4.10: The first four De Broglie harmonic electron orbits in the hydrogen atom.

Figure 4.10 shows the De Broglie standing electron waves, from left to right, from the lowest orbit, the "tonic" (n = 1), up to and including the 4th orbit (n = 4), the 3rd ‘harmonic’. Incidentally, I hope you will notice that these De Broglie orbits differ from standing waves on a vibrating string with fixed ends. One full wavelength fits on the lowest orbit, two full wavelengths fit on the next orbit, etc. Standing wave orbits with other than an integer number of wavelengths are not possible. This has to do with the fact that after having traveled a full orbit, the moving wave front must arrive exactly in phase with its ‘tail’ to interfere constructively. The electron wave just goes around and is not reflected on a fixed boundary as does happen on a vibrating string. Reflecting on fixed boundaries invokes 180 ophase shifts which correspond to half wavelengths. In short, only an integer number of wavelengths are allowed for circular standing waves [ 22 ].

Only four years later De Broglie's hypothesis became confirmed experimentally, albeit in a rather circuitous way. Coincidence – serendipity – played a major role.

The wave character of electrons was demonstrated in 1927 by Clinton Davisson (1881-1958) and Lester Germer (1896-1971) in experiments where electrons were reflected on a crystal lattice of nickel atoms. The results of their experiment, preferred directions in which the scattered electrons reflected, could only be explained with interference – which implied wave behavior. This is in fact the same line of thought that Young followed with his double-slit experiment in 1805. Interference presumes waves.

Two years after the confirmation of electron waves by Davisson and Germer, Louis De Broglie received the physics Nobel Prize in 1929. A well-earned recognition for his daring out-of-the-box thinking. For a good understanding of what the Davisson-Germer experiment entailed and what it confirmed, we should first pay some attention to diffraction grids.

Diffraction gratings or diffraction grids work along exactly the same principle as Young’s double-slit. The only practical difference is that diffraction grid results show considerably sharper lines (fringes) of a higher intensity. A diffraction grid consists of a great number of parallel slits with very small and precisely equal mutual distances. The earliest form of a diffraction grid was a smoke blacked glass plate where a large number of parallel scratches was carefully applied to the soot. When lit with parallel traveling waves of monochromatic light, coming from a distant source, each slit will function as a Huygens wave source vibrating synchronously with the other slits, all slits producing then synchronous circular extending waves. A positive lens focuses these waves on a screen. In very sharply defined directions the arriving waves will just differ exactly an integer number of wavelengths, thus creating constructive interference in the focal plane of the lens.

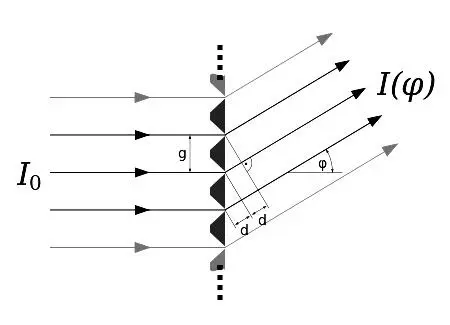
Figure 4.11: A diffraction grid with slits. Source: Wikimedia Commons.

At slightly different other angles destructive interference occurs, because of the out of phase contributions to the interference from all the waves originating from this multitude of slits. So, much sharper defined interference fringes will be obtained with a diffraction grid than with a simple double-slit. This is not restricted to the visible spectrum. With such diffraction grids the wavelengths of all kinds of EM-waves, can be measured with great precision. The geometric principle, where the angle that the light rays make with the slit holder determines the path length difference, is completely identical to the double-slit principle. See figure 4.11 for a representation of the path length differences that arise with a diffraction grid.