Paul J. van Leeuwen - Quantum Physics is NOT Weird

In figure 4.11, gis the distance between the slits, φis the angle at which the light is projected, and dis the path length difference between the waves originating from adjacent slits. The relationship between g, dand φcan be used to calculate the wavelength. Just for completeness, the equation is: sin (φ) = n.λ/gwhere nis the order number of the intensity maximum, the fringe, counted from the primary maximum in the middle.

But to understand what quantum physics wants to tell us, it isn’t necessary for you to memorize or even understand those equations. Forget them if you will. It’s not relevant in understanding the message of this book. Just remember that every diffraction grid or grating will produce interference effects in very distinct directions by causing synchronous wave sources departing from the slits.

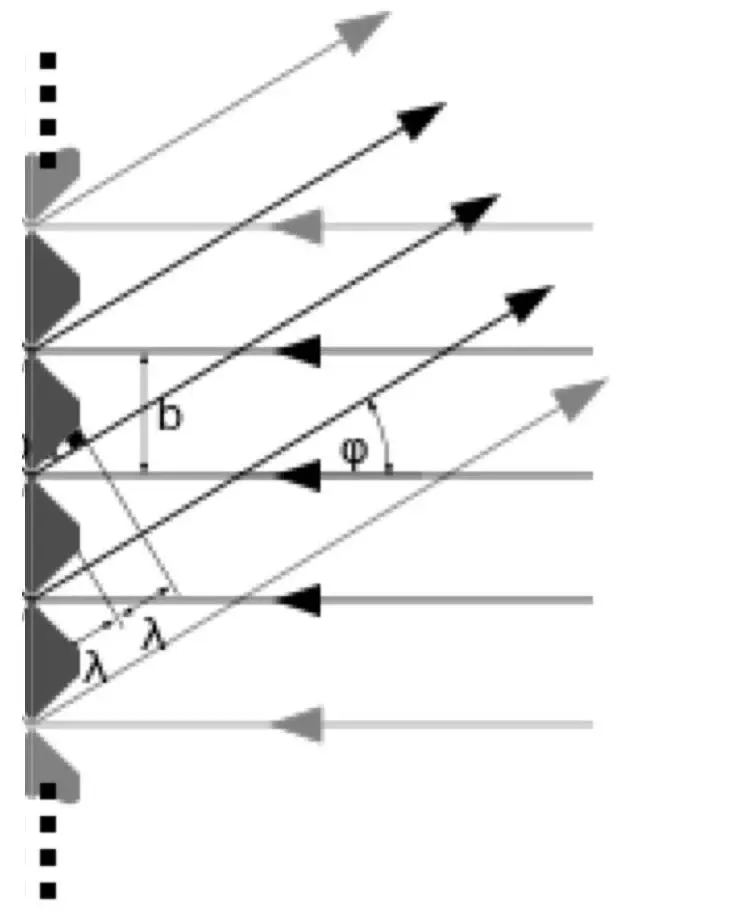
Figure 4.12: Reflection on a diffraction grid with grooves such as on a DVD.

Source: Wikimedia Commons.

Reflection of light on parallel grooves, such as with light falling on the tracks of a DVD, will produce the same diffraction effects. See figure 4.12. The principle as depicted in figure 4.11 is the same for reflection, only the incoming beam arrives in this case from the right and synchronous waves will travel back to the right.

This explains the rainbow-like effects that you observe when white light falls on a DVD. White light contains a range of different wavelengths (colors) which produce constructive and destructive interference at different angles so you will see colored fringes. In this case the lenses in our eyes are the focusing devices and the retinae in each eye act as the photosensitive screens.

Diffraction experiment [ 23 ]: You can try this for yourself with a DVD or CD. Use light from different sources, an incandescent lamp, a fluorescent lamp, and an LED lamp. What is the difference? Can you explain the difference? Can you roughly estimate the groove distance from what you observe if you know that yellow light has a wavelength of around 575 nanometers?

Serendipity often plays a role in important discoveries in physics. Remember Wilhelm Röntgen's discovery of X-rays because a screen with barium platinocyanide, that he happened to have standing somewhere in his lab, lit up. How wave behavior of electrons was confirmed experimentally is another excellent example of serendipity. From 1921 on Clinton Davisson did research into the atomic structure of metals. Apparently inspired by Rutherford's experiment with alpha particles and gold atoms, he bombarded metal with narrow beams of electrons and tried to glean some insights into the structure of the metal by measuring accurately the reflected intensity at different reflection angles.

Davisson devised a specially constructed vacuum device [ 24 ]that could produce a narrow electron beam aimed at a block of nickel fixed on a 360 orotatable holder. The reflected electrons were collected with an electron catcher with which the collected charge could be measured. This electron catcher could slide along a an arc of 90 o, so the varying intensity of the reflected electrons could be measured over angles between 0 oto 90 o. See figure 4.13. The 360 orotation of the nickel holder combined with the 90 oslide of the electron catcher meant that electron reflection from the nickel surface could be measured over an almost complete hemisphere. The entire device was housed in a vacuum glass enclosure.

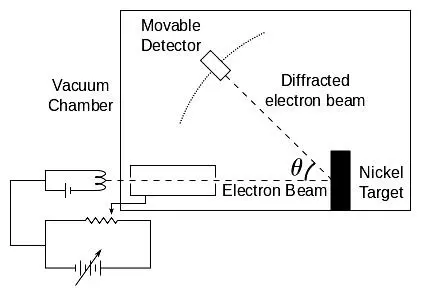
Figure 4.13: Davisson-Germer experiment principle.

Source: Wikimedia Commons.

Their first experiments with this device did not produce any very useful results. However, due to an accident - an explosion in the laboratory - the glass enclosure got damaged and air did enter. Davisson noted then that the smooth surface of the nickel target had become oxidized as a result of the accident. To repair the visible blemish, his assistant heated the nickel block and polished it in order to obtain a perfectly unblemished smooth target surface again.

However, the unintended effect of his treatment was that the surface of the nickel target now had become crystallized. Now their device suddenly produced interesting results. The measurements with the repaired device suddenly yielded results that indicated that the electrons were only reflected in specific directions. Their measurements indicated specific reflection angles showing maximum and minimum intensity, just like an interference pattern. But Davisson, thinking of electrons as little hard particles, did not understand how that could be. Despite not being able to grasp what the interference in his measurements really implied, he published his findings in Science, outlining his set-up and reporting his measurement results.

During a short holiday in 1926 with his family in England, Davisson attended a lecture of Max Born(1882-1970) in Oxford about recent developments in quantum physics. Born presented, to Davisson’s utter surprise, the results of Davisson’s experiment, published in Science. Born's interpretation of Davisson's results was that these confirmed De Broglie's hypothesis of electron waves because they showed interference effects brought about by a diffraction grid of nickel atoms. Understandably, Davisson could hardly wait to return to his laboratorium in the US. He probably already suspected a Nobel Prize waiting for him. He improved his device together with Germer so that the angles of reflection could be measured with greater accuracy, and also that the energy of the electrons could be controlled better, resumed his experiments, and got this time excellent results which he then published in Nature in 1927. By varying the voltage of the electron gun, he was able to control the energy and therefore the velocity of the electrons very precisely and thus also their wavelength according to the De Broglie relation: λ = h/(mv). From his interference results he could now determine the relationship between the wavelength of his electrons and the distance between the nickel atoms in the crystal lattice. The nickel atoms on the crystallized nickel surface apparently acted as a two-dimensional diffraction grid.

If necessary re-read for a better understanding of this effect the previous paragraph on diffraction grids.

In 1937, Davisson shared the Nobel Prize in physics [ 25 ]with George Paget Thomson(1892-1975) who demonstrated electron diffraction by shooting them through diffraction grids formed by very thin metal films with crystal structures. The experimental confirmation of the wave behavior of electrons gave the Bohr atomic model a firmer foothold, but the idea that particles also had a wave character caused serious headaches to many colleagues and other contemporaries. Classical Newtonian physics had still a firm hold on the minds of most physicists of that era, something that seems still to be the case today for the minds of scientists working in other fields than quantum physics. People still expect to see an objective world that behaves predictably and does not show itself from two contradictory aspects at the same time. Physics students were discouraged to philosophize about the strange paradoxes in quantum physics. As long as the results of their experiments matched their calculations it was ok. Which meant: "Shut up and calculate.". An admonition uttered by David Mermin, not by Richard Feymann, to set records straight. After all, quantum mechanics calculations did work extremely accurate, considering the successes which were achieved. So, why worry?