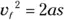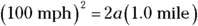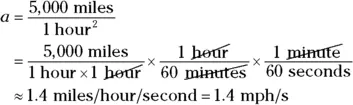Figuring out time and distance
Given a constant acceleration and the change in velocity, you can figure out both time and distance. For instance, imagine you’re a drag racer. Your acceleration is 26.6 meters per second 2, and your final speed is 146.3 meters per second. Now find the total distance traveled. Got you, huh? “Not at all,” you say, supremely confident. “Just let me get my calculator.”
You know the acceleration and the final speed, and you want to know the total distance required to get to that speed. This problem looks like a puzzler because the equations in this chapter have involved time up to this point. But if you need the time, you can always solve for it. You know the final speed, v f , and the initial speed, v i (which is zero), and you know the acceleration, a . Because 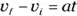 , you know that
, you know that

Now you have the time. You still need the distance, and you can get it this way:
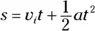
The second term drops out because 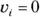 , so all you have to do is plug in the numbers:
, so all you have to do is plug in the numbers:
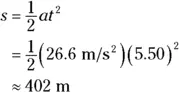
In other words, the total distance traveled is 402 meters, or a quarter-mile. Must be a quarter-mile racetrack.
Finding distance with initial velocity
Given initial velocity, time, and acceleration, you can find displacement. Here’s an example: There you are, the Tour de France hero, ready to give a demonstration of your bicycling skills. There will be a time trial of 8.0 seconds. Your initial speed is 6.0 meters/second, and when the whistle blows, you accelerate at 2.0 m/s 2for the 8.0 seconds allowed. At the end of the time trial, how far will you have traveled?
You could use the relation 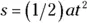 , except you don’t start off from zero speed — you’re already moving, so you should use the following:
, except you don’t start off from zero speed — you’re already moving, so you should use the following:
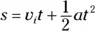
In this case, 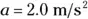 ,
, 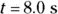 , and
, and 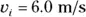 , so you get the following:
, so you get the following:
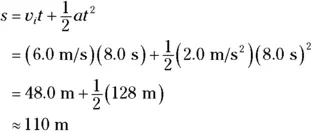
You write the answer to two significant digits — 110 meters — because you know the time only to two significant digits (see Chapter 2for info on rounding). In other words, you ride to victory in about 110 meters in 8.0 seconds. The crowd roars.
Linking Velocity, Acceleration, and Displacement
Say you want to relate displacement, acceleration, and velocity without having to know the time. Here’s how it works. First, you solve the acceleration formula for the time:
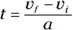
Because displacement is 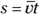 and average velocity is
and average velocity is 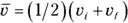 when the acceleration is constant, you can get the following equation:
when the acceleration is constant, you can get the following equation:
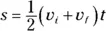
Substituting for the time, t , you get
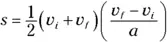
After doing the algebra and simplifying, you get
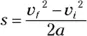
 Moving the 2 a to the other side of the equation, you get an important equation of motion:
Moving the 2 a to the other side of the equation, you get an important equation of motion:
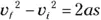
Whew! If you can memorize this one, you can relate velocity, acceleration, and displacement. Put this equation to work — you see it often in physics problems.
There you are, getting into your Physics racer as the crowd cheers. It’s time for some hefty acceleration. You get out your clipboard. What acceleration would you need to end up at 100 miles per hour at the end of a 1.0-mile racetrack?
Okay, you think. You need an equation that relates speed, acceleration, and displacement. It’s time for
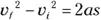
In this case, it’s even a little easier, because you know that the initial velocity is 0 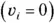 , so you have
, so you have
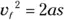
Well, well, it looks like the problem is half-solved. Putting in the numbers gives you
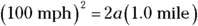
Now solve for a:

Miles per hour 2? What the heck kind of units are those? Change that to something more understandable, such as mph per second. To change one of the per-hour units to per-second, multiply by the conversion factor (see Chapter 2):
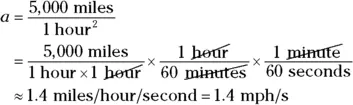
So your velocity would be increasing by only 1.4 mph every second — that’s not too outrageous — you’d feel a mild acceleration, that’s all.
Читать дальше

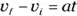 , you know that
, you know that
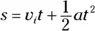
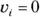 , so all you have to do is plug in the numbers:
, so all you have to do is plug in the numbers: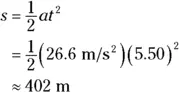
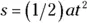 , except you don’t start off from zero speed — you’re already moving, so you should use the following:
, except you don’t start off from zero speed — you’re already moving, so you should use the following: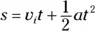
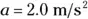 ,
, 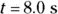 , and
, and 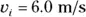 , so you get the following:
, so you get the following: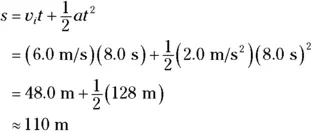
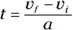
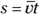 and average velocity is
and average velocity is 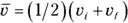 when the acceleration is constant, you can get the following equation:
when the acceleration is constant, you can get the following equation: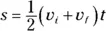
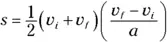
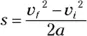
 Moving the 2 a to the other side of the equation, you get an important equation of motion:
Moving the 2 a to the other side of the equation, you get an important equation of motion: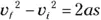
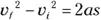
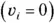 , so you have
, so you have