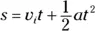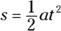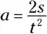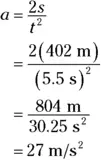Acceleration can be uniform or nonuniform. Nonuniform acceleration requires a change in acceleration. For example, when you’re driving, you encounter stop signs or stop lights often, and when you slow to a stop and then speed up again, you take part in nonuniform acceleration.
Other accelerations are very uniform (in other words, unchanging), such as the acceleration due to gravity near the surface of the Earth. This acceleration is 9.8 meters per second 2downward, toward the center of the Earth, and it doesn’t change (if it did, plenty of people would be pretty startled).
Relating Acceleration, Time, and Displacement
This chapter deals with four quantities of motion: acceleration, velocity, time, and displacement. You work the standard equation relating displacement and time to get velocity:
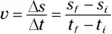
And you see the standard equation relating velocity and time to get acceleration:
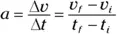
But both of these equations only go one level deep, relating velocity to displacement and time and acceleration to velocity and time. What if you want to relate acceleration to displacement and time? This section shows you how you can cut velocity out of the equation.
 When you’re slinging around algebra, you may find it easier to write single quantities like v (to stand for
When you’re slinging around algebra, you may find it easier to write single quantities like v (to stand for 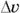 ) rather than
) rather than 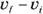 . You can usually turn v into
. You can usually turn v into  later if necessary.
later if necessary.
Not-so-distant relations: Deriving the formula
You relate acceleration, displacement, and time by messing around with the equations until you get what you want. First, note that displacement equals average velocity multiplied by time:
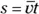
You have a starting point. But what’s the average velocity? If your acceleration is constant, your velocity increases in a straight line from 0 to its final value, as Figure 3-4 shows.
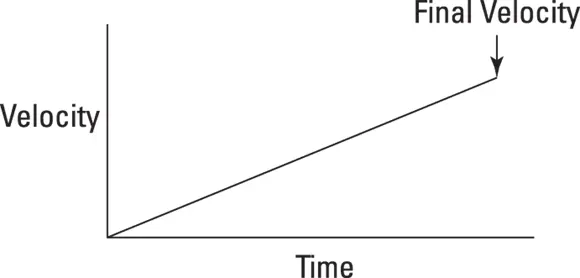
FIGURE 3-4: Increasing velocity under constant acceleration.
The average velocity is half the final velocity, and you know this because there’s constant acceleration. Your final velocity is 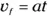 , so your average velocity is half this:
, so your average velocity is half this:
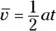
So far, so good. Now you can plug this average velocity into the 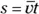 equation and get
equation and get
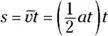
And this becomes
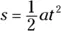
You can also put in  rather than just plain t:
rather than just plain t:
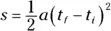
Congrats! You’ve worked out one of the most important equations you need to know when you work with physics problems relating acceleration, displacement, time, and velocity.
Notice that when you derived this equation, you had an initial velocity of zero. What if you don’t start off at zero velocity, but you still want to relate acceleration, time, and displacement? What if you’re initially going 100 miles per hour? That initial velocity would certainly add to the final distance you go. Because distance equals speed multiplied by time, the equation looks like this (don’t forget that this assumes the acceleration is constant):
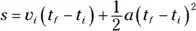
 You also see this written simply as the following (where t stands for
You also see this written simply as the following (where t stands for 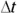 , the time over which the acceleration happened):
, the time over which the acceleration happened):
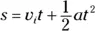
Calculating acceleration and distance
With the formula relating distance, acceleration, and time, you can find any of those values, given the other two. If you have an initial velocity, too, finding distance or acceleration isn’t any harder. In this section, we work through some physics problems to show you how these formulas work.
Given distance and time, you can find acceleration. Say you become a drag racer in order to analyze your acceleration down the dragway. After a test race, you know the distance you went — 402 meters, or about 0.25 miles (the magnitude of your displacement) — and you know the time it took — 5.5 seconds. So what was your acceleration as you blasted down the track?
Well, you know how to relate displacement, acceleration, and time (see the preceding section), and that’s what you want — you always work the algebra so that you end up relating all the quantities you know to the one quantity you don’t know. In this case, you have
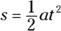
(Keep in mind that in this case, your initial velocity is 0 — you’re not allowed to take a running start at the drag race!) You can rearrange this equation with a little algebra to solve for acceleration; just divide both sides by t 2and multiply by 2 to get
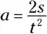
Great. Plugging in the numbers, you get the following:
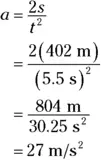
Okay, the acceleration is approximately 27 meters per second 2. What’s that in more understandable terms? The acceleration due to gravity, g , is — 9.8 meters per second 2, so this is about 2.7 g-force — you’d feel yourself pushed back into your seat with a force about 2.7 times your own weight.
Читать дальше

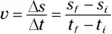
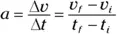
 When you’re slinging around algebra, you may find it easier to write single quantities like v (to stand for
When you’re slinging around algebra, you may find it easier to write single quantities like v (to stand for 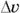 ) rather than
) rather than 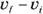 . You can usually turn v into
. You can usually turn v into  later if necessary.
later if necessary.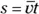

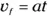 , so your average velocity is half this:
, so your average velocity is half this: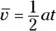
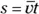 equation and get
equation and get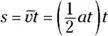
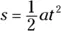
 rather than just plain t:
rather than just plain t: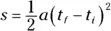
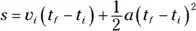
 You also see this written simply as the following (where t stands for
You also see this written simply as the following (where t stands for 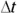 , the time over which the acceleration happened):
, the time over which the acceleration happened):