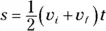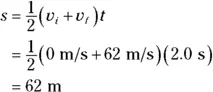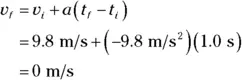
After 1.0 second, the ball has zero velocity because it’s reached the top of its trajectory, just at the point where it’s about to fall back down again. So the acceleration has actually slowed down the ball because it was going in the direction opposite the velocity.
Now see what happens as the ball falls back down to Earth. The ball has zero velocity, but the acceleration due to gravity accelerates the ball downward at a rate of –9.8 m/s 2. As the ball falls, it gathers speed before you catch it. What’s its final velocity as you catch it, given that its initial velocity at the top of its trajectory is zero?
The time for the ball to fall back down to you is just the same as the time it took to reach the top of its trajectory, which is 1.0 second, so you can find the final velocity for this part of the ball’s motion with this calculation:
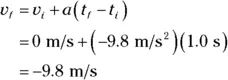
So the final velocity is 9.8 meters/second directed straight downward. The magnitude of this velocity — that is, the speed of the ball — is 9.8 meters/second. The acceleration increases the speed of the ball as it falls because the acceleration is in the same direction as the velocity for this part of the ball’s trajectory.
 When you work with physics problems, bear in mind that acceleration can speed up or slow down an object, depending on the direction of the acceleration and the velocity of the object. Don’t simply assume that just because something is accelerating its speed must be increasing. (By the way, if you want to see an example of how an acceleration can leave the speed of an object unchanged, take a look at the circular motion topic covered in Chapter 7.)
When you work with physics problems, bear in mind that acceleration can speed up or slow down an object, depending on the direction of the acceleration and the velocity of the object. Don’t simply assume that just because something is accelerating its speed must be increasing. (By the way, if you want to see an example of how an acceleration can leave the speed of an object unchanged, take a look at the circular motion topic covered in Chapter 7.)
Examining average and instantaneous acceleration
Just as you can examine average and instantaneous speeds and velocities, you can also examine average and instantaneous acceleration. Average acceleration is the ratio of the change in velocity to the change in time. You calculate average acceleration, also written as 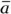 , by taking the final velocity, subtracting the initial velocity, and dividing the result by the total time (final time minus the initial time):
, by taking the final velocity, subtracting the initial velocity, and dividing the result by the total time (final time minus the initial time):
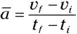
 At any given point, the acceleration you measure is the instantaneous acceleration, and that number can be different from the average acceleration. For example, when you first see red flashing police lights behind you, you may jam on the brakes, which gives you a big acceleration, in the direction opposite to which you’re moving (in everyday parlance, you’d say you just decelerated , but that term’s a no-no in physics circles). But you ease up on the gas pedal a little and coast to a stop, so the acceleration is smaller. The average acceleration, however, is a single value, derived by dividing the overall change in velocity by the overall time.
At any given point, the acceleration you measure is the instantaneous acceleration, and that number can be different from the average acceleration. For example, when you first see red flashing police lights behind you, you may jam on the brakes, which gives you a big acceleration, in the direction opposite to which you’re moving (in everyday parlance, you’d say you just decelerated , but that term’s a no-no in physics circles). But you ease up on the gas pedal a little and coast to a stop, so the acceleration is smaller. The average acceleration, however, is a single value, derived by dividing the overall change in velocity by the overall time.
 Acceleration is the rate of change of velocity, not speed. If a velocity’s direction changes without a change in speed, this is also a kind of acceleration.
Acceleration is the rate of change of velocity, not speed. If a velocity’s direction changes without a change in speed, this is also a kind of acceleration.
Taking off: Putting the acceleration formula into practice
Here’s an acceleration example. As they strap you into the jet on the aircraft carrier deck, the mechanic says you need to take off at a speed of at least 62.0 m/s. You’ll be catapulted at an acceleration of 31 m/s 2. Is there going to be enough catapult to do the job? You ask how long the catapult is. “A hundred meters,” says the mechanic, finishing strapping you in.
Hmm, you think. Will an acceleration of 31 m/s 2over a distance of 100 meters do the trick? You take out your clipboard and ask yourself: How far must I be accelerated at 31 m/s 2to achieve a speed of 62 m/s?
First think of the distance that you need to be accelerated over as the size of the displacement from your initial position. To find this displacement, you can use the equation 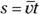 , where s is the displacement, is the average velocity, and t is the time — which means you have to find the time over which you’re accelerated. For that, you can use the equation that relates change in velocity,
, where s is the displacement, is the average velocity, and t is the time — which means you have to find the time over which you’re accelerated. For that, you can use the equation that relates change in velocity, 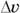 , acceleration a , and change in time,
, acceleration a , and change in time, 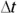 :
:
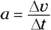
Solving for 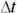 gives you
gives you
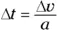
Plugging in the numbers and solving gives you the change in time:
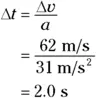
Okay, so it takes 2.0 seconds for you to reach a speed of 62 m/s if your rate of acceleration is 31 m/s 2. Now you can use this equation to find the total distance you need to travel to get up to this speed; it is the size of the displacement, which is given by  , where
, where 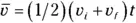 ,
, 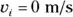 , and
, and 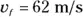 . So your equation is
. So your equation is
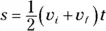
Plugging in the numbers gives you
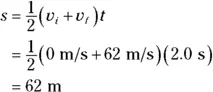
So it will take 62 meters of 31 m/s 2acceleration to get you to takeoff speed — and the catapult is 100 meters long. No problem.
Understanding uniform and nonuniform acceleration
Читать дальше

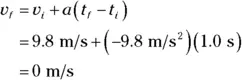
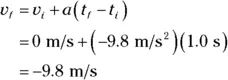
 When you work with physics problems, bear in mind that acceleration can speed up or slow down an object, depending on the direction of the acceleration and the velocity of the object. Don’t simply assume that just because something is accelerating its speed must be increasing. (By the way, if you want to see an example of how an acceleration can leave the speed of an object unchanged, take a look at the circular motion topic covered in Chapter 7.)
When you work with physics problems, bear in mind that acceleration can speed up or slow down an object, depending on the direction of the acceleration and the velocity of the object. Don’t simply assume that just because something is accelerating its speed must be increasing. (By the way, if you want to see an example of how an acceleration can leave the speed of an object unchanged, take a look at the circular motion topic covered in Chapter 7.)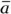 , by taking the final velocity, subtracting the initial velocity, and dividing the result by the total time (final time minus the initial time):
, by taking the final velocity, subtracting the initial velocity, and dividing the result by the total time (final time minus the initial time):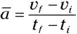
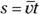 , where s is the displacement, is the average velocity, and t is the time — which means you have to find the time over which you’re accelerated. For that, you can use the equation that relates change in velocity,
, where s is the displacement, is the average velocity, and t is the time — which means you have to find the time over which you’re accelerated. For that, you can use the equation that relates change in velocity, 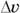 , acceleration a , and change in time,
, acceleration a , and change in time, 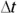 :
: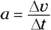
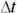 gives you
gives you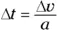
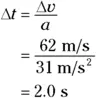
 , where
, where 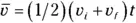 ,
, 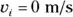 , and
, and 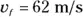 . So your equation is
. So your equation is