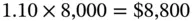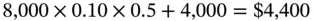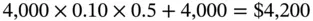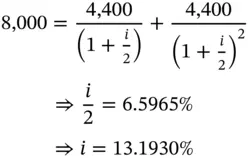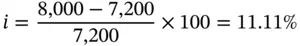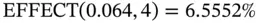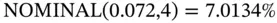Financial institutions employ a variety of techniques to calculate the interest on the loans taken from them by borrowers. Thus the interest rate that is effectively paid by a borrower may be very different from what is being quoted by the lender. 1
The Simple Interest Approach
If the lender were to use a simple interest approach, then borrowers need only pay interest for the actual period of time for which they have used the funds. Each time they make a partial repayment of the principal, the interest due will come down for subsequent periods.
Michael has borrowed $8,000 from a bank for a year. The bank charges simple interest at the rate of 10% per annum. If the loan is repaid in one lump sum at the end of the year, the amount payable will be:
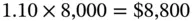
This consists of $8,000 by way of principal repayment and an interest payment of $800.
Now let us consider a case where Michael repays the principal in two equal semiannual installments. For the first six months, interest will be computed on the entire principal. So the first installment will be:
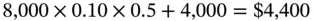
The second installment will be lower, for it will include interest only on the remaining principal, which in this case is $4,000. So the amount repayable will be:
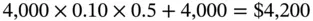
The sum of the two payments is $8,600. In the first case the interest payable was $800, whereas in the second case it is only $600. Quite obviously, the more frequently principal is repaid, the lower will be the amount of interest.
This approach entails the calculation of interest on the entire principal. The sum total of principal and interest is then divided by the number of installments in which the loan is sought to be repaid. As should be obvious, if the loan is repaid in a single annual installment, the total interest payable will be $800 and the effective rate of interest will be 10%. However, if Michael were to repay in two equal semiannual installments of $4,400 each, the effective rate of interest may be computed as follows:
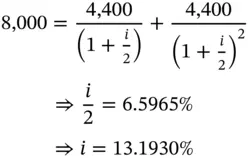
In the case of such loans, interest is first computed on the entire loan amount. It is then deducted from the principal, and the balance is lent to the borrower, who has to repay the entire principal at maturity. Such loans are usually repaid in a single installment. Let us take the example of Michael.
The interest for the loan amount of $8,000 is $800. So the lender will give him $7,200 and ask him to repay $8,000 after a year. The effective rate of interest is:
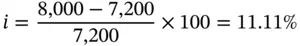
LOANS WITH A COMPENSATING BALANCE
Many banks require borrowers to keep a percentage of the loan amount as a deposit with them. Such deposits, referred to as compensating balances, earn little or no interest. Obviously such requirements will increase the effective rate of interest, and the higher the required balance, the greater will be the rate of interest that is paid by the borrower.
Assume that in Michael's case, the bank required a compensating balance of 12.50%. So while he will have to pay interest on the entire loan amount of $8,000, the usable amount is only $7,000.
The effective rate of interest is:

TIME VALUE OF MONEY–RELATED FUNCTIONS IN EXCEL
We will first demonstrate how to compute effective rates given nominal rates, and vice versa.
Mary has borrowed money from a bank, which is quoting a rate of 6.4% per annum compounded quarterly. To calculate the effective annual rate, we use an Excel function called EFFECT. The parameters are:
Nominal_rate: This is the nominal rate of interest per annum.
Npery: This is the frequency of compounding per annum.
The nominal rate is 6.40% or 0.064 in this case. The frequency of compounding per annum is 4. Using the function, we get the effective annual rate of 6.5552% per annum.
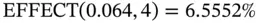
If we are given the effective rate, we can compute the equivalent nominal rate using the NOMINAL function in Excel. The parameters are
Effect_rate: This is the effective rate of interest per annum.
Npery: This is the frequency of compounding per annum.
Assume that the bank is quoting an effective annual rate of 7.2% per annum with quarterly compounding. What is the equivalent nominal annual rate? In this case the effective rate is 7.20%, and the frequency of compounding is 4. Thus,
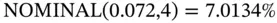
The Future Value (FV) Function in Excel
To compute the future value using Excel, we need to use the FV function. The parameters are:
Rate: Rate is the periodic interest rate.
Nper: Nper is the number of periods.
Pmt: Pmt stands for the periodic payment, and is not applicable in this case because there are no periodic cash flows. Thus, we can either put a zero, or an extra comma in lieu.
Pv: Pv stands for the present value, or the initial investment. We input it with a negative sign in order to ensure that the answer is positive. In many Excel functions, cash flows in one direction are positive while those in the opposite direction are negative. Thus, if the investment is positive, the subsequent inflow is negative, and vice versa. In this case, if we specify a negative number for the present value, we get the future value with a positive sign. If, however, the present value is given with a positive sign, the future value, although it would have the same magnitude, would have a negative sign.
Type: This is a binary variable, which is either 0 or 1. It is not required at this stage, and we can just leave it blank.
Rosalyn has deposited $20,000 with a bank for five years. The bank has agreed to pay 4.8% interest per annum compounded annually. How much can she withdraw at the end?
We will invoke the function as, FV(.048,5,,−20000) and the answer is $25,283.45. In this function we are inputting an extra comma in lieu of the value for Pmt. As an alternative we could have given the value as zero.
Now assume that the bank is quoting a rate of 4.8% per annum with quarterly compounding. The periodic interest rate is 1.20%, and the number of quarterly periods in five years is 20. The future value may be computed as follows.
Читать дальше