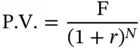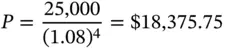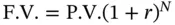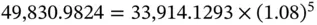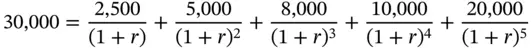Note 4:The FVIF is given in the form of tables in most textbooks, for integer values of the interest rate and number of time periods. If, however, either the interest rate or the number of periods is not an integer, then we cannot use such tables and would have to rely on a scientific calculator or a spreadsheet.
Future value calculations entailed the determination of the terminal value of an initial investment. Sometimes, however, we may seek to do the reverse. That is, we may have a terminal value in mind, and seek to calculate the quantum of the initial investment that will result in the desired terminal cash flow, given an interest rate and investment horizon. Thus, in this case, instead of computing the terminal value of a given principal, we seek to compute the principal that corresponds to a given terminal value. The principal amount that is obtained in this fashion is referred to as the present value of the terminal cash flow.
The Mechanics of Present Value Calculation
Take the case of an investor who wishes to have $ F after N periods. The periodic interest rate is r %, and interest is compounded once per period. Our objective is to determine the initial investment that will result in the desired terminal cash flow. Quite obviously
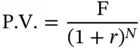
where P.V. is the present value of $F.
Patricia wants to deposit an amount of $ P with her bank in order to ensure that she has $25,000 at the end of four years. If the bank pays 8% interest per annum compounded annually, how much does she have to deposit today?
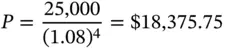
The expression 1/(1 + r ) Nis the amount that must be invested today if we are to have $1 at the end of N periods, if the investment were to pay interest at the rate of r % per period. It is called the PVIF (Present Value Interest Factor). It too depends only on two variables, namely the interest rate per period and the number of periods. If we know the PVIF for a given interest rate and time horizon, we can compute the present value of any terminal cash flow by simply multiplying the quantum of the cash flow by the factor. The process of finding the principal corresponding to a given future amount is called discounting and the interest rate that is used is called the discount rate . Quite obviously, there is a relationship between the present value factor and the future value factor, for assumed values of the interest rate and the time horizon. One factor is simply a reciprocal of the other.
HANDLING A SERIES OF CASH FLOWS
Let us assume that we wish to compute the present value or the future value of a series of cash flows, for a given interest rate. The first cash flow will arise after one period, and the last will arise after N periods. In such a situation, we can simply find the present value of each of the component cash flows and add up the terms in order to compute the present value of the entire series. The same holds true for computing the future value of a series of cash flows. Thus present values and future values are additive in nature.
Let us consider the vector of cash flows shown in Table 2.3. Assume that the interest rate is 8% per annum, compounded annually. Our objective is to compute the present value and future value of the entire series.
TABLE 2.3Vector of Cash Flows
| Year |
Cash Flow |
| 1 |
2,500 |
| 2 |
5,000 |
| 3 |
8,000 |
| 4 |
10,000 |
| 5 |
20,000 |
The present and future value of the series is depicted in Table 2.4. As can be seen, we have simply computed the present and future value of each term in the series, and summed up the values.
TABLE 2.4Present and Future Values of the Cash Flows
| Year |
Cash Flow |
Present Value |
Future Value |
| 1 |
2,500 |
2,314.8148 |
3,401.2224 |
| 2 |
5,000 |
4,286.6941 |
6,298.5600 |
| 3 |
8,000 |
6,350.6579 |
9,331.2000 |
| 4 |
10,000 |
7,350.2985 |
10,800.0000 |
| 5 |
20,000 |
13,611.6639 |
20,0000.0000 |
|
Total Value |
33,914.1293 |
49,830.9824 |
While computing the present value of each cash flow we have to discount the amount so as to obtain the value at time “0.” Thus the first year's cash flow has to be discounted for one year, whereas the fifth year's cash flow has to be discounted for five years. On the other hand, while computing the future value of a cash flow we have to find its terminal value as at the end of five years. Consequently, the cash flow arising after one year has to be compounded for four years, whereas the final cash flow, which is received at the end of five years, does not have to be compounded.
There is a relationship between the present value of the vector of cash flows as a whole and its future value. It may be stated as:
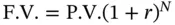
In this case
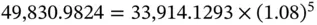
THE INTERNAL RATE OF RETURN
Consider a deal where we are offered the vector of cash flows depicted in Table 2.4, in return for an initial investment of $30,000. The question is, what is the rate of return that we are being offered? The rate of return r is obviously the solution to the following equation.
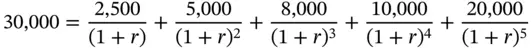
The solution to this equation is termed as the Internal Rate of Return. It can be obtained using the IRR function in EXCEL. In this case the solution is 11.6106%.
Note 5: A Point About Effective Rates
Let us assume that we are asked to compute the present value or future value of a series of cash flows arising every six months, and are given a rate of interest quoted in annual terms, without the frequency of compounding being specified. The normal practice is to assume semiannual compounding. That is, we would divide the annual rate by two to determine the periodic interest rate for discounting or compounding. In other words, the quoted interest rate per annum will be treated as the nominal rate and not as the effective rate.
Consider the series of cash flows depicted in Table 2.5. Assume that the annual rate of interest is 8%.
TABLE 2.5Vector of Cash Flows
| Period |
Cash Flow |
| 6 months |
2,000 |
| 12 months |
2,500 |
| 18 months |
3,500 |
| 24 months |
7,000 |
The present value will be calculated as
Читать дальше