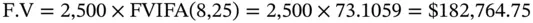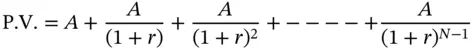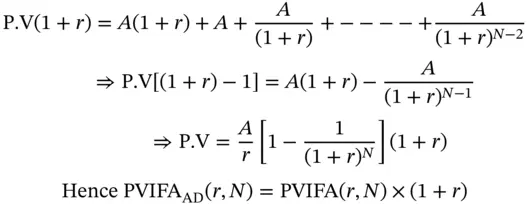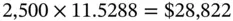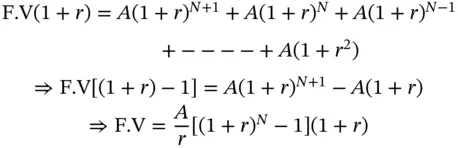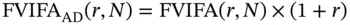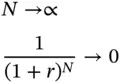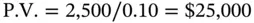Sunil K. Parameswaran - Fundamentals of Financial Instruments
Здесь есть возможность читать онлайн «Sunil K. Parameswaran - Fundamentals of Financial Instruments» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Fundamentals of Financial Instruments
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:3 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Fundamentals of Financial Instruments: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Fundamentals of Financial Instruments»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
, renowned finance trainer Sunil Parameswaran delivers a comprehensive introduction to the full range of financial products commonly offered in the financial markets. Using clear, worked examples of everything from basic equity and debt securities to complex instruments—like derivatives and mortgage-backed securities – the author outlines the structure and dynamics of the free-market system and explores the environment in which financial instruments are traded. This one-of-a-kind book also includes: New discussions on interest rate derivatives, bonds with embedded options, mutual funds, ETFs, pension plans, financial macroeconomics, orders and exchanges, and Excel functions for finance Supplementary materials to enhance the reader’s ability to apply the material contained within A foundational exploration of interest rates and the time value of money
is the ideal resource for business school students at the undergraduate and graduate levels, as well as anyone studying financial management or the financial markets. It also belongs on the bookshelves of executive education students and finance professionals seeking a refresher on the fundamentals of their industry.

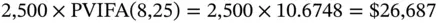
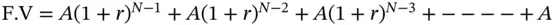
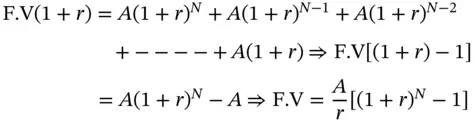
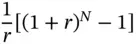 is called the Future Value Interest Factor Annuity (FVIFA) . This is the future value of an annuity that pays $1 per period for N periods, where interest is compounded at the rate of r % per period. The advantage once again is that if we know the factor, we can calculate the future value of any annuity that pays $ A per period.
is called the Future Value Interest Factor Annuity (FVIFA) . This is the future value of an annuity that pays $1 per period for N periods, where interest is compounded at the rate of r % per period. The advantage once again is that if we know the factor, we can calculate the future value of any annuity that pays $ A per period.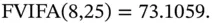 Thus the future value is:
Thus the future value is: