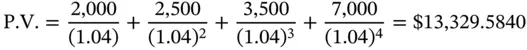
Similarly the future value will be
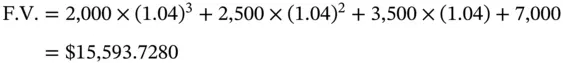
However, if it were to be explicitly stated that the effective annual rate is 8%, then the calculations would change. The semiannual rate that corresponds to an effective annual rate of 8% is  . The present value will then be given by
. The present value will then be given by
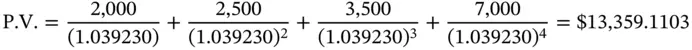
Similarly, the future value will then be given by
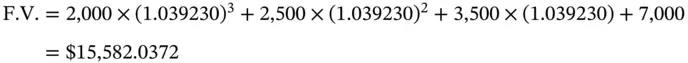
The present value is higher when we use an effective annual rate of 8% for discounting. This is because the lower the discount rate, the higher will be the present value; obviously, an effective annual rate of 8% is lower than a nominal annual rate of 8% with semiannual compounding. Because the interest rate that is used is lower, the future value at the end of four half-years is lower when we use an effective annual rate of 8%.
In this case, if we were to calculate the IRR for the given cash flow stream, we would get a semiannual rate of return. We would then have to multiply it by two to get the annual rate of return. The IRR for this cash flow stream, assuming an initial investment of $12,500, is 6.2716%. The IRR in annual terms is therefore 12.5432%.
Kapital Markets is offering an instrument that will pay $25,000 after four years in return for an initial investment of $12,500. Alfred is a potential investor, who requires a rate of return of 12% per annum. The issue is, is the offer attractive from his perspective? There are three ways of approaching this problem.
The Future Value Approach
Let us assume that Alfred buys this instrument for $12,500. If the rate of return received by him were to be 12%, he would have to receive a future value of $19,669. This can be stated as:
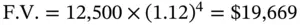
If Alfred were to receive a higher terminal payment, his rate of return would be higher than 12%, else it would be lower. Because the instrument offered to him promises a terminal value of $25,000, which is greater than the required future value of $19,669, the investment is attractive from his perspective.
The Present Value Approach
The present value of $25,000 using a discount rate of 12% per annum is:
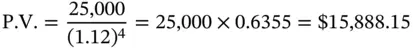
The rate of return, if one were to make an investment of $15,888.15 in return for a payment of $25,000 four years hence, is 12%. If the investor were to pay a lower price at the outset, he would earn a rate of return that is higher than 12%, whereas if he were to invest more, he would obviously earn a lower rate of return. In this case Alfred is being asked to invest $12,500, which is less than $15,288.15. Consequently, the investment is attractive from his perspective.
The Rate of Return Approach
If Alfred were to pay $12,500 in return for a cash flow of $25,000 after four years, his rate of return may be computed as:

Since the actual rate of return obtained by Alfred is greater than the required rate of return of 12%, the investment is attractive.
Not surprisingly, all three approaches lead to the same decision.
ANNUITIES: AN INTRODUCTION
An annuity is a series of payments made at equally spaced intervals of time. If all the payments are identical, then we term it as a Level Annuity. Examples include insurance premiums and monthly installments on housing loans and automobile loans, which are paid off by way of equal installments over a period of time.
If the first payment is made or received at the end of the first period, then we call it an ordinary annuity. Examples include salary, which will be paid only after an employee completes his duties for the month, and house rent, which will be usually paid by the tenant only at the end of the month. The interval between successive payments is called the payment period . We will assume that the payment period is the same as the interest conversion period. That is, if the annuity pays annually, we will assume annual compounding, whereas if it pays semiannually we will assume half-yearly compounding. This assumption is not mandatory and, in practice, we can easily handle cases where the payment period is longer than the interest conversion period, as well as instances where it is shorter.
Consider a level annuity that makes periodic payments of $A for N periods. On a timeline the cash flows can be depicted as shown in Figure 2.1. The point in time at which we are is depicted as time 0 .

FIGURE 2.1Timeline for an Annuity
Assume that the applicable interest rate per period is r %. We can then calculate the present and future values as shown here.
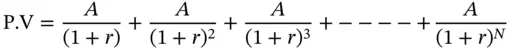
Therefore,
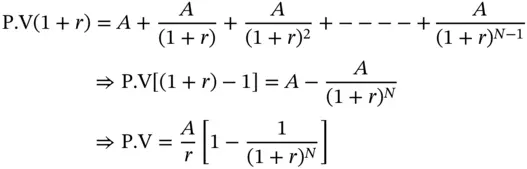
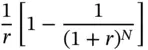 is called the Present Value Interest Factor Annuity (PVIFA) . PVIFA(r,N) is the present value of an annuity that pays $1 at periodic intervals for N periods, computed using a discount rate of r %. Thus, like the factors that we studied earlier, it too depends on the interest rate and the number of periods. The present value of any annuity that pays $A per period can therefore be computed by multiplying A by the appropriate value of PVIFA.
is called the Present Value Interest Factor Annuity (PVIFA) . PVIFA(r,N) is the present value of an annuity that pays $1 at periodic intervals for N periods, computed using a discount rate of r %. Thus, like the factors that we studied earlier, it too depends on the interest rate and the number of periods. The present value of any annuity that pays $A per period can therefore be computed by multiplying A by the appropriate value of PVIFA.
Alpha Technologies is offering a financial instrument to Alfred that promises to pay $2,500 per year for 25 years, beginning one year from now. Alfred requires an annual rate of return of 8%. The question is, what is the maximum price that he will be prepared to pay?
 . Thus the value of the payments is:
. Thus the value of the payments is:
Читать дальше

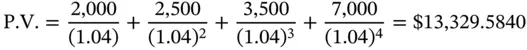
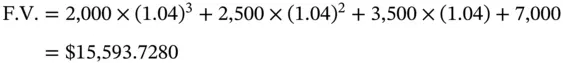
 . The present value will then be given by
. The present value will then be given by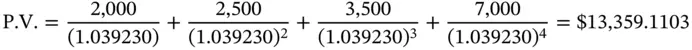
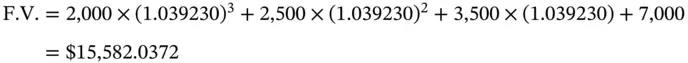
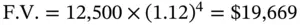
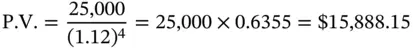


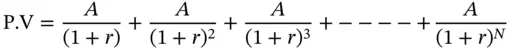
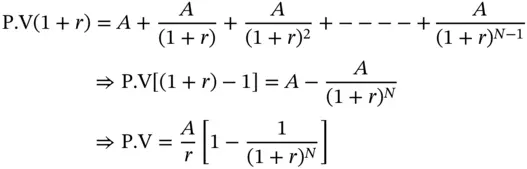
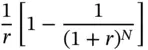 is called the Present Value Interest Factor Annuity (PVIFA) . PVIFA(r,N) is the present value of an annuity that pays $1 at periodic intervals for N periods, computed using a discount rate of r %. Thus, like the factors that we studied earlier, it too depends on the interest rate and the number of periods. The present value of any annuity that pays $A per period can therefore be computed by multiplying A by the appropriate value of PVIFA.
is called the Present Value Interest Factor Annuity (PVIFA) . PVIFA(r,N) is the present value of an annuity that pays $1 at periodic intervals for N periods, computed using a discount rate of r %. Thus, like the factors that we studied earlier, it too depends on the interest rate and the number of periods. The present value of any annuity that pays $A per period can therefore be computed by multiplying A by the appropriate value of PVIFA. . Thus the value of the payments is:
. Thus the value of the payments is:










