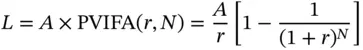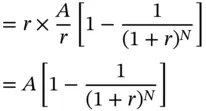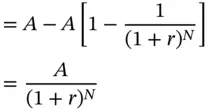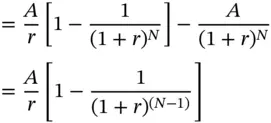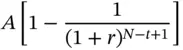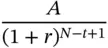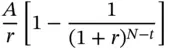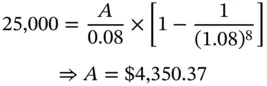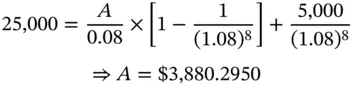Take the case of a loan which is repaid in N installments of $ A each. We will denote the original loan amount by L , and the periodic interest rate by r . Thus this is an annuity with a present value of L , which is repaid in N installments.
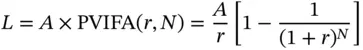
The interest component of the first installment
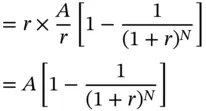
The principal component
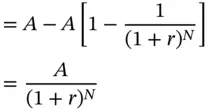
The outstanding balance at the end of the first payment
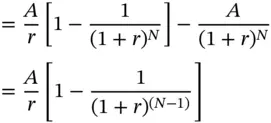
In general, the interest component of the ‘t’ th installment is
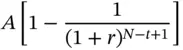
The principal component of the ‘t’ th installment is
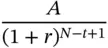
and the outstanding balance at the end of the ‘t’ th payment is
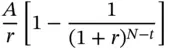
Sylvie has borrowed $25,000 from First National Bank and has to pay it back in eight equal annual installments. If the interest rate is 8% per annum on the outstanding balance, what is the installment amount, and what will the amortization schedule look like?
Let us denote the unknown installment amount by A . We know that
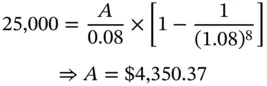
We will analyze the first few entries in Table 2.6in order to clarify the principles involved. At time 0 , the outstanding principal is $25,000. After one period, a payment of $4,350.37 will be made. The interest due for the first period is 8% of $25,000, which is $2,000. Consequently, the excess payment of $2,350.37 represents a partial repayment of principal. Once this amount is repaid and adjusted toward the principal, the outstanding balance at the end of the first period will become $22,649.63. At the end of the second period, the second installment of $4,350.37 will be paid. The interest due for this period is 8% of the outstanding balance at the start of the period, which is $22,649.63. Thus the interest component of the second installment is $1,811.97. The balance, which is $2,538.40, constitutes a partial repayment of principal. The value of the outstanding principal at the end should be zero. As can be seen, the outstanding principal declines after each installment payment. Because the payments themselves are constant, the interest component will steadily decline while the principal component will steadily increase.
TABLE 2.6An Amortization Schedule
| Year |
Payment |
Interest |
Principal Repayment |
Outstanding Principal |
| 0 |
|
|
|
25,000 |
| 1 |
4,350.37 |
2,000.00 |
2,350.37 |
22,649.63 |
| 2 |
4,350.37 |
1,811.97 |
2,538.40 |
20,111.23 |
| 3 |
4,350.37 |
1,608.90 |
2,741.47 |
17,369.76 |
| 4 |
4,350.37 |
1,389.58 |
2,960.79 |
14,408.97 |
| 5 |
4,350.37 |
1,152.72 |
3,197.65 |
11,211.32 |
| 6 |
4,350.37 |
896.91 |
3,453.46 |
7,757.86 |
| 7 |
4,350.37 |
620.63 |
3,729.74 |
4,028.12 |
| 8 |
4,350.37 |
322.25 |
4,028.12 |
0.00 |
Thus, in the case of such loans, the initial installments will consist largely of interest payments. As we approach the maturity of the loan, however, the corresponding installments will consist largely of principal repayments.
AMORTIZATION WITH A BALLOON PAYMENT
Julie Tate has taken a loan of $25,000 from First National Bank. The loan requires her to pay in eight equal annual installments along with a terminal payment of $5,000. This terminal payment that has to be made over and above the scheduled installment in year eight is termed as a balloon payment. The interest rate is 8% per annum on the outstanding principal. The annual installment may be calculated as follows.
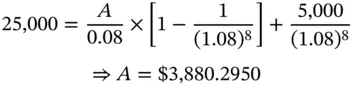
Obviously the larger the balloon, the smaller will be the periodic installment payment for a given loan amount. The amortization schedule may be depicted as shown in Table 2.7.
TABLE 2.7Amortization with a Balloon Payment
| Year |
Payment |
Interest |
Principal Repayment |
Outstanding Principal |
| 0 |
|
|
|
25,000 |
| 1 |
3,880.2950 |
2,000.00 |
1,880.30 |
23,119.70 |
| 2 |
3,880.2950 |
1,849.58 |
2,030.72 |
21,088.99 |
| 3 |
3,880.2950 |
1,687.12 |
2,193.18 |
18,895.81 |
| 4 |
3,880.2950 |
1,511.66 |
2,368.63 |
16,527.18 |
| 5 |
3,880.2950 |
1,322.17 |
2,558.12 |
13,969.06 |
| 6 |
3,880.2950 |
1,117.52 |
2,762.77 |
11,206.29 |
| 7 |
3,880.2950 |
896.50 |
2,983.79 |
8,222.50 |
| 8 |
8,880.2950 |
657.80 |
8,222.50 |
0.00 |
THE EQUAL PRINCIPAL REPAYMENT APPROACH
Sometimes a loan may be structured in such a way that the principal is repaid in equal installments. Thus, the principal component of each installment will remain constant; however, as in the case of the amortized loan, the interest component of each payment will steadily decline, on account of the diminishing loan balance. Therefore, the total magnitude of each payment will also decline.
We will illustrate the payment stream for an eight-year loan of $25,000, assuming that the interest rate is 8% per annum ( Table 2.8).
TABLE 2.8Equal Principal Repayment Schedule
| Year |
Payment |
Interest |
Principal Repayment |
Outstanding Principal |
| 0 |
|
|
|
25,000 |
| 1 |
5,125 |
2,000 |
3,125 |
21,875 |
| 2 |
4,875 |
1,750 |
3.125 |
18,750 |
| 3 |
4,625 |
1,500 |
3,125 |
15,625 |
| 4 |
4,375 |
1,250 |
3,125 |
12,500 |
| 5 |
4,125 |
1,000 |
3,125 |
9,375 |
| 6 |
3,875 |
750 |
3,125 |
6,250 |
| 7 |
3,625 |
500 |
3,125 |
3,125 |
| 8 |
3,375 |
250 |
3,125 |
0.00 |
TYPES OF INTEREST COMPUTATION
Читать дальше