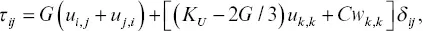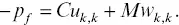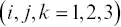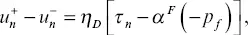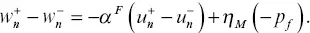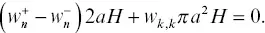Compared with the changes in the Young's modulus during the scCO 2injection, shear modulus and its related attenuation were largely unchanged during the experiment ( Fig. 5.6).
This indicates that the observed changes in the Young's modulus are attributed to the mechanical, poroelastic effect, rather than changes in the rock's mineral properties caused by chemical interactions with the injected scCO 2.
Saturation of the pore space by scCO 2was determined by obtaining CT images of the cores for (1) initial dry state (pore space filled with air), (2) water‐saturated state, and (3) partially scCO 2saturated state. Knowing the densities of the fluids contained in the pore space, the average scCO 2saturation within each CT imaging voxel was computed via linear interpolation.
For intact cores ( Fig. 5.7, top left columns), scCO 2migrated more or less uniformly but with higher saturations within layers containing larger pores (because of the stronger capillary entry pressure in the smaller pores) along the bedding planes. For core‐parallel fractures, the mated fracture (Frac Ia) contributed to somewhat localized distribution of scCO 2. However, the scCO 2was still well dispersed throughout the core, possibly because the void space within the fracture was highly disconnected and did not result in an efficient fast path for the scCO 2.
In contrast, for core‐parallel fractures with large shear displacement (Frac Ib and Frac Id are shown in Fig. 5.7), almost all the scCO 2migrated through the fracture, and little scCO 2infiltrated into the rock matrix. Also, because of the large aperture of the fracture (~0.54 mm), the vertically oriented fracture in Frac Id exhibited preferential pooling of lighter scCO 2in water along the top edge of the fracture by the buoyancy effect.
For a core‐perpendicular fracture, the migration behavior of scCO 2was initially similar to the intact core, exhibiting a wide distribution of the fluid across the core with preferential flow along the bedding planes. However, the fracture (aperture ~0.26 mm) served as a trap and accumulated scCO 2before the second half of the core was infiltrated.
In this section, we will examine the experimentally observed behavior of Young's modulus and related attenuation during scCO 2injection.
5.4.1. Gassmann Model Interpretation of Young's Modulus Behavior
Detailed dynamic poroelastic modeling of the experimental results is beyond the scope of this chapter. However, we can gain some insights into the observed behavior of fractured samples using a simple, isotropic, quasi‐static model (i.e., isotropic Gassmann model).
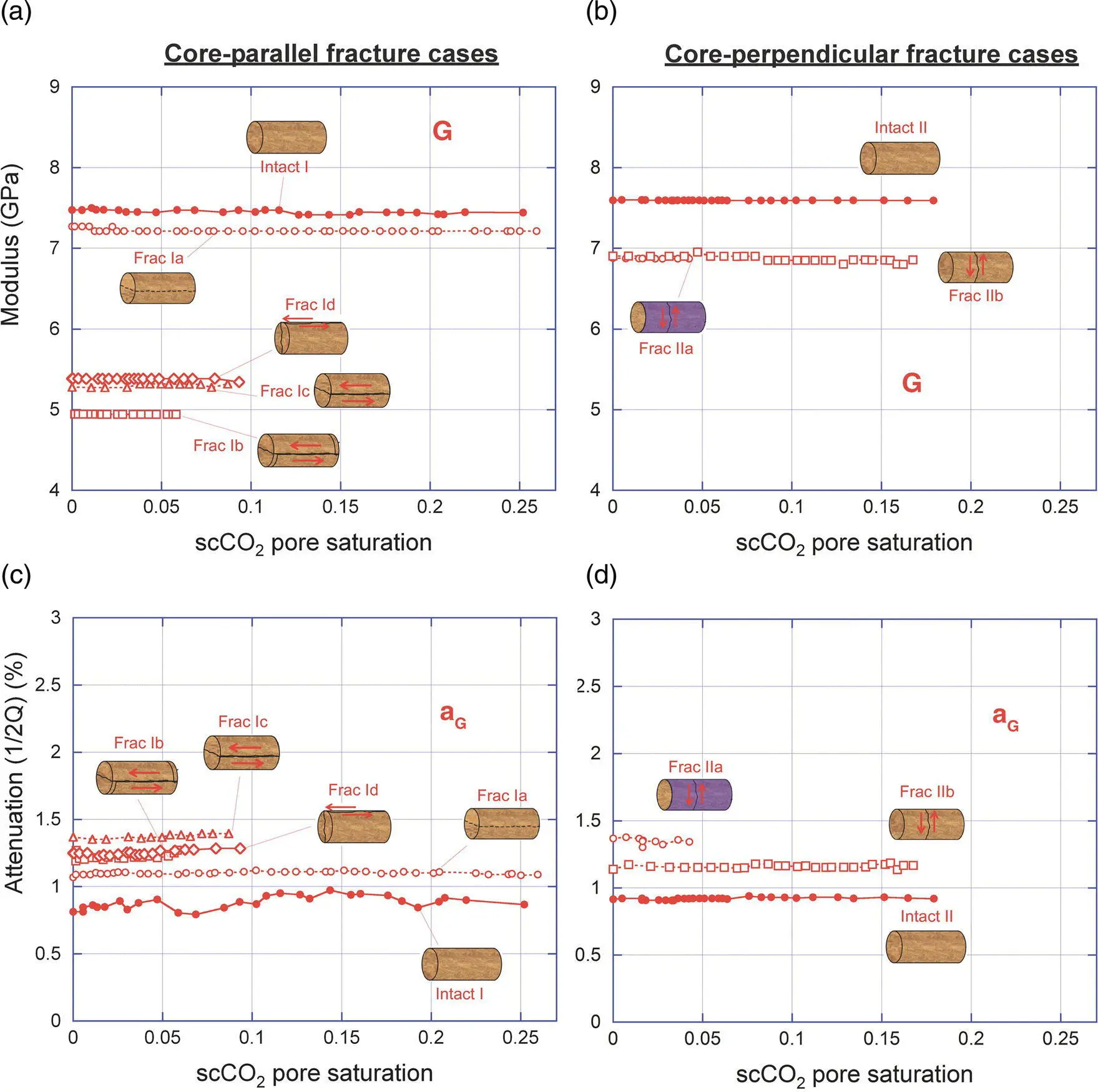
Figure 5.6 Shear modulus and related attenuations determined from SHRB tests during scCO 2injection experiments on Carbon Tan sandstone cores: (a) Carbon Tan #1 elastic moduli; (b) Carbon Tan #2 elastic moduli; (c) Carbon Tan #1 attenuations; (d) Carbon Tan #2 attenuations.
In the following, we consider only small stress and displacement perturbations caused by seismic waves. For the porous, intact matrix of the sandstone samples, we assume the following constitutive equations for an isotropic homogeneous poroelastic medium (e.g., Pride et al., 2002):
(5.3) 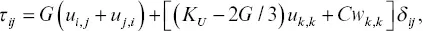
(5.4) 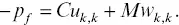
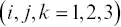

Figure 5.7 X‐ray CT images of scCO 2invasion into intact and fractured sandstone cores. Brighter colors indicate higher CO 2saturation. Average apertures determined from CT images are indicated for open, sheared fractures. (Note that at the top of the Frac IIb images, unintended shifts of the experimental setup between an initial calibration scan and subsequent scans during the scCO 2injection experiment resulted in false images of scCO 2along the bottom edge of the core, which disappear in the subsequent images.)
In 5.3and 5.4, repeated indices indicate summation, and, i≡ ∂ / ∂x i. u iis the local average solid frame displacement vector. w i≡ φ ( U i‐ u i) is the relative fluid volume displacement vector defined via u i, local average fluid displacement vector in the pore space U i, and porosity φ . δ ijindicates an identity tensor. τ ijis the total stress tensor, and p fis the fluid pressure (positive sign for compression). G is the solid frame shear modulus, and K Uis the undrained bulk modulus. C and M are the Biot's coupling and fluid storage moduli, respectively. Note that these parameters are related via C = αM , K U= K D+ α 2 M , K D =( 1 ‐αB) K U, where α is the Biot‐Willis coefficient, B is the Skempton coefficient, and K Dis the drained bulk modulus. For the fracture part, assuming a plane, permeable, and compliant fracture, the boundary conditions for the fracture‐normal displacement, stress, and pressure can be stated as (Nakagawa & Schoenberg, 2007)
(5.5) 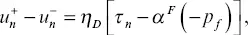
(5.6) 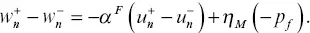
The superscripts “ +” and “ –” indicate the opposing surfaces of the fracture, and subscript “ n ” indicates the direction perpendicular (normal) to the fracture plane. The effect of fluid flow parallel to the fracture is neglected. The thickness of the fracture h is assumed to be very small compared wih the diameter of the sample. Also note that the effective stress coefficient of the open, permeable fracture α Fcan be assumed to be 1. η Dand η Mare the specific drained normal fracture compliance and the specific fracture storage compliance. For an open fracture, η Mcan be computed via η M= h / M F~ h / K f, where M Fis the storage modulus of the material within the fracture, and K fis the bulk modulus of the fluid contained in the fracture (the fracture porosity φ Fis 1).
From here on, we will use Cartesian coordinates with the 3 axis aligned with the core axis. First, we compute low‐frequency Young's modulus for a jacketed cylindrical core with a radius a and a height H , containing a single fracture along its axis. Conservation of fluid mass in the core requires that the fluid volume exchanged between the fracture and the matrix be in balance:
(5.7) 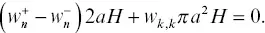
Читать дальше