Geophysical Monitoring for Geologic Carbon Storage

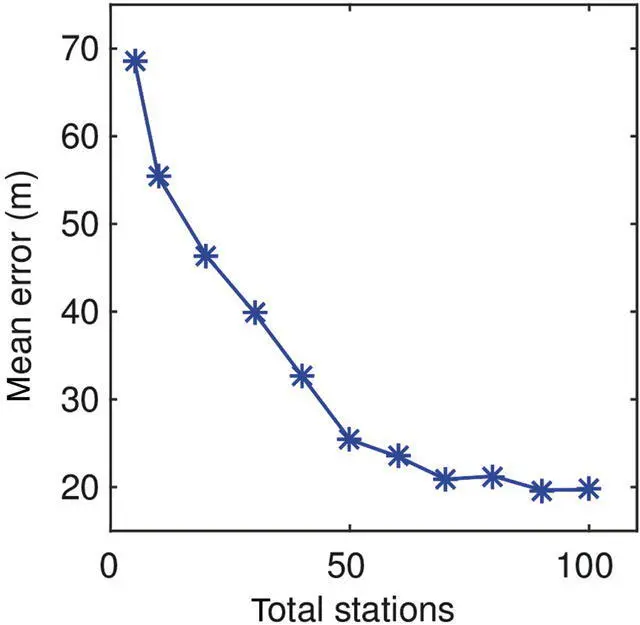
Figure 4.12 Event location accuracy versus the total number of geophones for optimal design of a borehole geophone array in Figure 4.10.

We have developed a methodology for the optimal design of seismic networks for monitoring induced microseismic events during CO 2injection and storage. Based on the location of the target monitoring region where induced microseismic events may occur, we design a regularly spaced surface seismic array within an area centered at the target monitoring region, or regularly spaced borehole geophone array above the target monitoring region. We vary the number of seismic stations/borehole geophones, and compute the event location accuracy using both absolute and differential travel times. The optimal seismic network is determined using the trade‐off curve between the mean location accuracy and the number of seismic stations. We have demonstrated our methodology using a synthetic model for the Kimberlina CO 2storage demonstration site in California. Our results show that for the specifically defined monitoring regions in this study, it needs approximately 20 surface seismic stations or 50 geophones for cost‐effective monitoring. These demonstration examples assume that seismic events of interest can be recorded by all stations within the network. Similar approaches can be applied to different scales of microseismic monitoring problems depending on the detectability of the smallest seismic events needed to monitor. For the same total number of seismic stations, irregularly spaced seismic stations produce similar results to those obtained with regularly spaced seismic stations, as long as they have good enough azimuthal and distance coverage. Three‐component seismic stations are recommended over one‐component seismic stations to include more accurate readings of S‐wave arrival times to improve the locations of microseismic events.

This research was supported by the U.S. Department of Energy (DOE) through the Los Alamos National Laboratory (LANL), which is operated by Triad National Security, LLC, for the National Nuclear Security Administration (NNSA) of U.S. DOE under Contract No. 89233218CNA000001. The work was part of the National Risk Assessment Partnership of the Carbon Storage Program managed by the National Energy Technology Laboratory. We thank William Foxall for providing us with the initial velocity model for the Kimberlina site. We thank two anonymous reviewers for their valuable comments.

1 Birkholzer, J. T., Zhou, Q., Cortis, A., & Finsterle, S. (2011). A sensitivity study on regional pressure buildup from large‐scale CO2 storage projects. Energy Procedia, 4, 4371–4378.

2 Boullenger, B., Verdel, A., Paap, B., Thorbecke, J., & Draganov, D. (2015). Studying CO2 storage with ambient‐noise seismic interferometry: A combined numerical feasibility study and field‐data example for Ketzin, Germany. Geophysics, 80(1), Q1–Q13. https://doi.org/10.1190/geo2014‐0181.1

3 Chatelain, J.‐L., Roecker, S. W., Hatzfeld, D., & Molnar, P. (1980). Microearthquake seismicity and fault plane solutions in the Hindu Kush region and their tectonic implications. Journal of Geophysical Research, 85(B3), 1365–1387.

4 Coblentz, D., Lee, R., Wilson, J., & Bradley, C. (2014). Kimberlina, California site characterization for applications to potential induced seismicity. Technical Report. Los Alamos National Laboratory.

5 Eisner, L., Hulsey, B. J., Duncan, P., Jurick, D., Werner, H., & Keller, W. (2010). Comparison of surface and borehole locations of induced seismicity. Geophysical Prospecting, 58(5), 809–820. https://doi.org/10.1111/j.1365‐2478.2010.00867.x

6 Ellsworth, W. L. (2013). Injection‐induced earthquakes. Science, 341(6142). https://doi.org/10.1126/science.1225942

7 Gomberg, J. S., Shedlock, K. M., & Roecker, S. W. (1990). The effect of S‐wave arrival times on the accuracy of hypocenter estimation. Bulletin of the Seismological Society of America, 80(6A), 1605–1628.

8 Husen, S., Kissling, E., Deichmann, N., Wiemer, S., Giardini, D., & Baer, M. (2003). Probabilistic earthquake location in complex three‐dimensional velocity models. Journal of Geophysical Research: Solid Earth, 108(B2). https://doi.org/10.1029/2002JB001778

9 Kaven, J. O., Hickman, S. H., McGarr, A. F., & Ellsworth, W. L. (2015). Surface monitoring of microseismicity at the Decatur, Illinois, CO2 sequestration demonstration site. Seismological Research. Letters, 86(4), 1096–1101. https://doi.org/10.1785/0220150062

10 Kijko, A. (1977a). An algorithm for the optimum distribution of a regional seismic network: I, Pure and Applied Geophysics, 115(4), 999–1009.

11 Kijko, A. (1977b). An algorithm for the optimum distribution of a regional seismic network: II, an analysis of the accuracy of location of local earthquakes depending on the number of seismic stations. Pure and Applied Geophysics, 115(4), 1011–1021.

12 Kissling, E. (1988). Geotomography with local earthquake data. Reviews of Geophysics, 26(4), 659–698.

13 Lin, G., & Shearer, P. (2005). Tests of relative earthquake location techniques using synthetic data. Journal of Geophysical Research, 110(B4). https://doi.org/10.1029/2004JB003380

14 Maxwell, S. C., & Urbancic, T. I. (2001). The role of passive microseismic monitoring in the instrumented oil field. The Leading Edge, 20(6), 636–639.

15 Miyazawa, M., Venkataraman, A., Snieder, R., & Payne, M. A. (2008). Analysis of microearthquake data at Cold Lake and its applications to reservoir monitoring. Geophysics, 73(3), 15–21.

16 Oye, V., Aker, E., Daley, T. M., Kühn, D., Bohloli, B., & Korneev, V. (2013). Microseismic monitoring and interpretation of injection data from the in Salah CO2 storage site (Krechba), Algeria. Energy Procedia, 37, 4191–4198. https://doi.org/10.1016/J.EGYPRO.2013.06.321

17 Paige, C. C., & Saunders, M. A. (1982). LSQR: An algorithm for sparse linear equations and sparse least squares. ACM Transactions on Mathematical Software, 8(1), 43–71.

18 Pesicek, J. D., Child, D., Artman, B., & CieśBlik, K. (2014). Picking versus stacking in a modern microearthquake location: Comparison of results from a surface passive seismic monitoring array in Oklahoma. Geophysics, 79(6), KS61–KS68. https://doi.org/10.1190/geo2013‐0404.1

19 Rabinowitz, N., & Steinberg, D. M. (1990). Optimal configuration of a seismographic network: A statistical approach. Bulletin of the Seismological Society of America, 80(1), 187–196.

20 Steinberg, D. M., Rabinowitz, N., Shimshoni, Y., & Mizrachi, D. (1995). Configuring a seismographic network for optimal monitoring of fault lines and multiple sources. Bulletin of the Seismological Society of America, 85(6), 1847–1857.

21 Stork, A., Nixon, C., Hawkes, C., Birnie, C., White, D., Schmitt, D., & Roberts, B. (2018). Is CO2 injection at Aquistore aseismic? A combined seismological and geomechanical study of early injection operations. International Journal of Greenhouse Gas Control, 75, 107–124. https://doi.org/10.1016/J.IJGGC.2018.05.016

22 Takagishi, M., Hashimoto, T., Toshioka, T., Horikawa, S., Kusunose, K., Xue, Z., & Hovorka, S. D. (2017). Optimization study of seismic monitoring network at the CO2 injection site: Lessons learnt from monitoring experiment at the Cranfield Site, Mississippi, U.S.A. Energy Procedia, 114, 4028–4039. https://doi.org/10.1016/J.EGYPRO.2017.03.1543

23 Verdon, J. P., Kendall, J.‐M., & White, D. J. (2012). Monitoring carbon dioxide storage using passive seismic techniques. Proceedings of the Institution of Civil Engineers: Energy, 165(2), 85–96. https://doi.org/10.1680/ener.10.00018