John Paul Mueller - Algorithms For Dummies

Many people have a problem using recursion because they can’t easily visualize how it works. In most cases, you call a Python function, it does something, and then it stops. However, in recursion, you call a Python function, it does something, and then it calls itself repeatedly until the task reaches a specific condition — but all those previous calls are still active. The calls unwind themselves one at a time until the first call finally ends with the correct answer, and this unwinding process is where most people encounter a problem. Figure 4-1 shows how recursion looks when using a flow chart.

Notice the conditional in the center. To make recursion work, the function must have such a conditional or it could become an endless loop. The conditional determines one of two things:

The conditions for ending recursion haven’t been met, so the function must call itself again.

The conditions for ending recursion have been met, so the function returns a final value that is used to calculate the ending result.

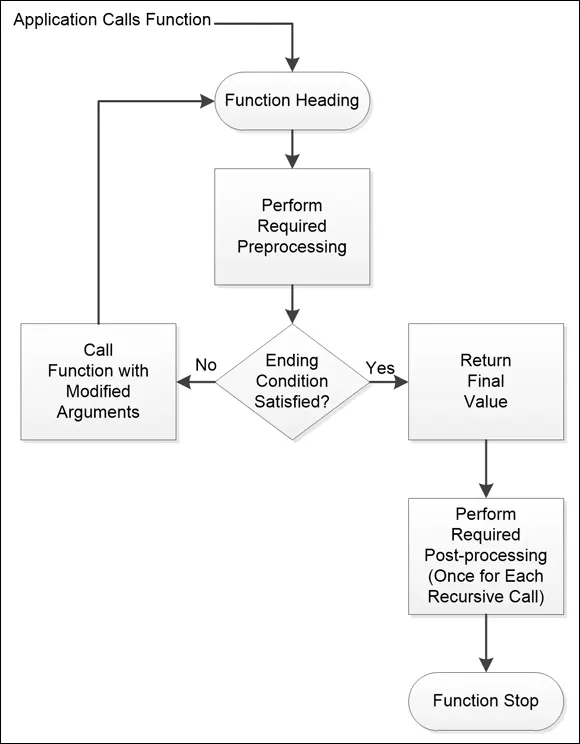
FIGURE 4-1:In the recursion process, a function continuously calls itself until it meets a condition.

When a function calls itself, it doesn’t use the same arguments that were passed to it. If it continuously used the same arguments, the condition would never change and the recursion would never end. Consequently, recursion requires that subsequent calls to the function must change the call arguments in order to bring the function closer to an ending solution.

One of the most common examples of recursion for all programming languages is the calculation of a factorial. A factorial is the multiplication of a series of numbers between a starting point and an ending point in which each number in the series is one less than the number before it. For example, to calculate 5! (read as five factorial), you multiple 5 * 4 * 3 * 2 * 1. The calculation represents a perfect and simple example of recursion. Here’s the Python code you can use to perform the calculation.

def factorial(n): print("factorial called with n = ", str(n)) if n == 1 or n == 0: print("Ending condition met.") return 1 else: return n * factorial(n-1) print(factorial(5))

Here is the output you see when running this example:

factorial called with n = 5factorial called with n = 4factorial called with n = 3factorial called with n = 2factorial called with n = 1Ending condition met.120

The code meets the ending condition when n == 1. Each successive call to factorial()uses factorial(n-1), which reduces the starting argument by 1. The output shows each successive call to factorial and the meeting of the final condition. The result, 120, equals 5! (five factorial).

It's important to realize that there isn’t just one method for using recursion to solve a problem. As with any other programming technique, you can find all sorts of ways to accomplish the same thing. For example, here’s another version of the factorial recursion that uses fewer lines of code but effectively performs the same task:

def factorial(n): print("factorial called with n = ", str(n)) if n > 1: return n * factorial(n-1) print("Ending condition met.") return 1 print(factorial(5))

Note the difference. Instead of checking the ending condition, this version checks the continuation condition. As long as nis greater than 1, the code will continue to make recursive calls. Even though this code is shorter than the previous version, it's also less clear because now you must think about what condition will end the recursion.

Many forms of recursion rely on a tail call. In fact, the first example in the previous section does. A tail call occurs any time the recursion makes a call to the function as the last thing before it returns. In the previous section, the line return n * factorial(n-1)is the tail call.

Tail calls aren’t necessarily bad, and they represent the manner in which most people write recursive routines. However, using a tail call forces Python to keep track of the individual call values until the recursion rewinds. Each call consumes memory. At some point, the system will run out of memory and the call will fail, causing your algorithm to fail as well. Given the complexity and huge datasets used by some algorithms today, tail calls can cause considerable woe to anyone using them.

With a little fancy programming, you can potentially eliminate tail calls from your recursive routines. You can find a host of truly amazing techniques online, such as the use of a trampoline, as explained at https://blog.moertel.com/posts/2013-06-12-recursion-to-iteration-4-trampolines.html . (Mind you, this isn’t the sort of trampoline you jump on at home!) However, the simplest approach to take when you want to eliminate recursion is to create an iterative alternative that performs the same task. For example, here is a factorial()function that uses iteration instead of recursion to eliminate the potential for memory issues:

def factorial(n): print("factorial called with n = ", str(n)) result = 1 while n > 1: result = result * n n = n - 1 print("Current value of n is ", str(n)) print("Ending condition met.") return result print(factorial(5))

The output looks very similar to before:

factorial called with n = 5Current value of n is 4Current value of n is 3Current value of n is 2Current value of n is 1Ending condition met.120

The basic flow of this function is the same as the recursive function. A whileloop replaces the recursive call, but you still need to check for the same condition and continue looping until the data meets the condition. The result is the same. However, replacing recursion with iteration is nontrivial in some cases, as explored in the example at https://blog.moertel.com/posts/2013-06-03-recursion-to-iteration-3.html .

Obviously, getting tasks done as quickly as possible is always ideal. However, you always need to carefully weigh the techniques you use to achieve this efficiency. Trading a little memory to perform a task faster is great as long as you have the memory to spare. Later chapters in the book explore all sorts of ways to perform tasks faster, but you can try some essential techniques no matter what sort of algorithm you're working with at any given time. The following sections explore some of these techniques.

Some problems look overwhelming when you start them. Take, for example, writing a book. If you consider the entire book, writing it is an overwhelming task. However, if you break the book into chapters and consider just one chapter, the problem seems a little more doable. Of course, an entire chapter can seem a bit daunting, too, so you break the task down into first-level headings, which seems even more doable, but still not quite doable enough. The first-level headings could contain second-level headings and so on until you have broken down the problem of writing about a topic into short articles as much as you can. This is how divide and conquer works. You break a problem down into smaller problems until you find a problem that you can solve without too much trouble.