Helmut Igl - Der Sudoku-Knacker

Zusätzlich zu diesem Vorgang werden jetzt auch noch die beiden letztmöglichen Zahlenberücksichtigt (siehe Grafik nächste Seite).

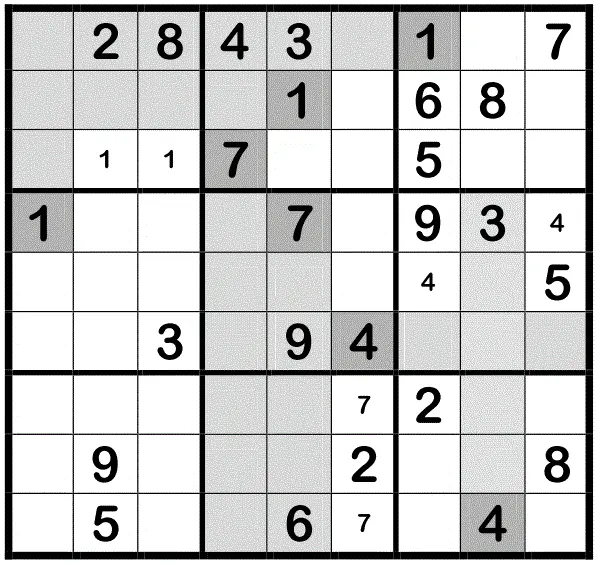
Im Beispiel sieht man, dass in Quadrant Q1 für die Zahl 1nur noch zweifreie Felder übriggeblieben sind. Dies sind die beiden letztmöglichen in diesem Quadranten, in denen eine Eins vorkommen kann. In diese Felder wird nun jeweils eine „1“ mit Bleistift eingetragen.

Einedieser beiden sog. Duplex-Zahlenist dann letztlich die „Echte“.

Bleiben mehr als zwei freie Felder übrig, wird nichts eingetragen.

Danach wird dieser Scan-Vorgang der Reihe nach mit den Zahlen 2 – 9 durchgeführt.

(Im Beispiel sind neben Scan 1noch Scan 7und z. T. Scan 4dargestellt.)

Eine gute Möglichkeit, die beiden letzten freien Felder beim Scannen leichter erkennen zu können, ist das Abdecken der zu beobachtenden Zeilen und Spalten mit dem Schreibstift.

Die Duplex-Zahlen sind in dieser Anleitung zur besseren Übersicht etwas kleiner dargestellt. Sie schreiben diese Zahlen bitte jedoch in ähnlicher Größe wie die Echten, denn kleine Zahlen kommen später noch zum Einsatz.

So würde das Sudoku nach dem Eintrag aller Duplex-Zahlen aussehen:

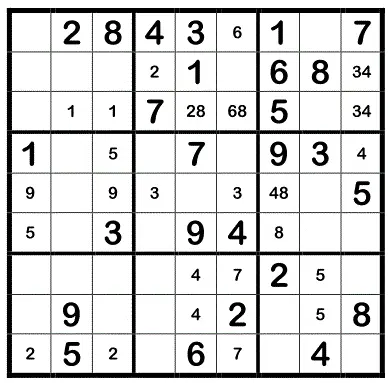
Welche Besonderheitensich in Zusammenhang mit den Duplex-Zahlen ergeben, wird in den nächsten Beispielen aufgezeigt.

Für die Beschreibung des Lösungsweges für alle Beispiel-Sudokus werden folgende Abkürzungenverwendet:

Selbstverständlich genügt zum Verständnis der Regeln diese bebilderte Anleitung. Die vielen Grafiken unterstützen sie dabei.

Sollten Sie jedoch die hier aufgezeigten Lösungswege auch auf Papier nachvollziehen wollen, können Sie sich die 20 Beispiele, falls Sie die Möglichkeit haben, von der Internetseite

https://www.dropbox.com/s/jeokgtod49hgfmz/Beispiele.pdf?dl=0

als PDF-Datei unter „Direkter Download“ herunterladen und danach ausdrucken oder Sie wenden sich kurz an den Verlag (s. Impressum).

Beispiel 1

Lösungsschritte:

Man scannt als Erstes die Zahl 1 und trägt (soweit das möglich ist) sowohl alle echten(mit Kugelschreiber o. Ä.) als auch die Duplex-Einsen(mit Bleistift) nach dem oben beschriebenen Muster in das Sudoku ein.

Scannen der Zahl 1 ( Scan 1): ergibt eine echte 1in Q2

Scan 2:ergibt eine echte 2in Q2 und zwei Duplex-Zweien (D2) in Q6+7.

Scan 3:D3 in Q4+8.

Scan 4:D4 in Q4

Scan 5:echte 5in Q5 und D5 in Q8 und …

…hier kommt es zu einer Besonderheitbezüglich der Duplex-Zahlen:

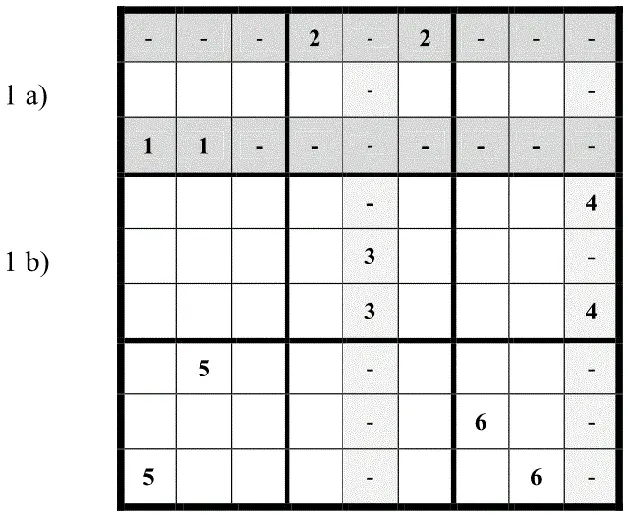
Nachdem es sich bei den Duplex-Zahlen immer um die beiden letztmöglichen Zahlen in einem Quadranten handelt, musseine der beiden die Echtesein.

Je nachdem, wie sie nun in ihren Quadranten angeordnet sind (waagrecht oder senkrecht), sperren die beiden die gesamte Zeile bzw. die gesamte Spalte, in der sie stehen.

In diesen Fällen werden die beiden Duplex-Zahlen zusammen praktisch wie eineEchte behandelt.

Daraus folgt:

Regel 1:

1a)Stehen zwei Duplex-Zahlen in einer Zeile nebeneinander(waagrecht), sperren sie die gesamte Zeilefür diese Zahl.

2a)Stehen zwei Duplex-Zahlen in einer Spalte untereinander(senkrecht), sperren sie die gesamte Spaltefür diese Zahl.

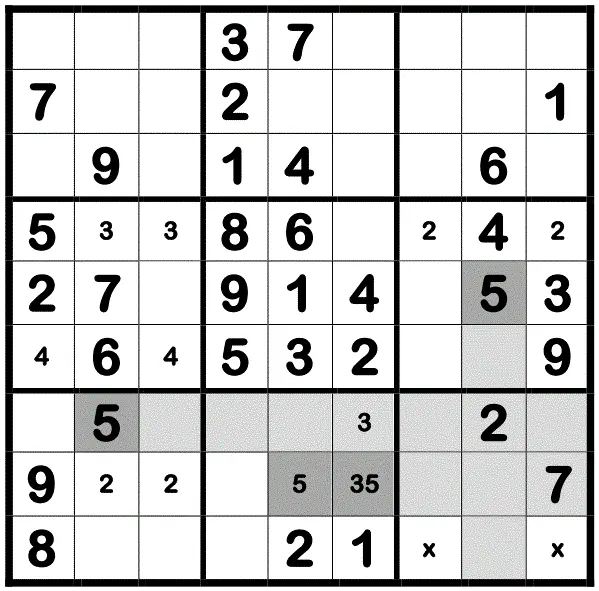
In unserem Beispiel bedeutet das unter Anwendung der Regel 1 a), dass die beiden Duplex-Fünfen in Q8 die 8. Zeile komplett für alle weiteren Fünfen blockieren. Dies ermöglicht uns den Eintrag zweier Duplex-Fünfen in Q9 (an den mit „x“ gekennzeichneten Feldern).

Zur Vermeidung von Fehlern hat es sich als sehr sinnvoll erwiesen, grundsätzlich nach jedem Zahlenscan die Position jeder gerade ermittelten echten oder Duplex-Zahl noch einmal zu überprüfen, ob sie auch in die richtigen Felder eingetragen wurden.

Sollte sich tatsächlich ein Fehler eingeschlichen haben, können wir ihn an dieser Stelle noch rechtzeitig berichtigen. Entdeckt man einen Fehler erst zu einem späteren Zeitpunkt ist es oft nicht mehr möglich, ihn zurückzuverfolgen. D. h. man muss mit dem Sudoku nochmals von vorne beginnen!

Wir machen weiter mit:

Scan 6: 6in Q6,

D6 in Q2 und Q9

Scan 7: 7in Q3 und Q6,

D7 in Q5 und Q7

Scan 8:D8 in Q5

→ 8in Q6 und Q4,

→ D8 in Q1 und Q9

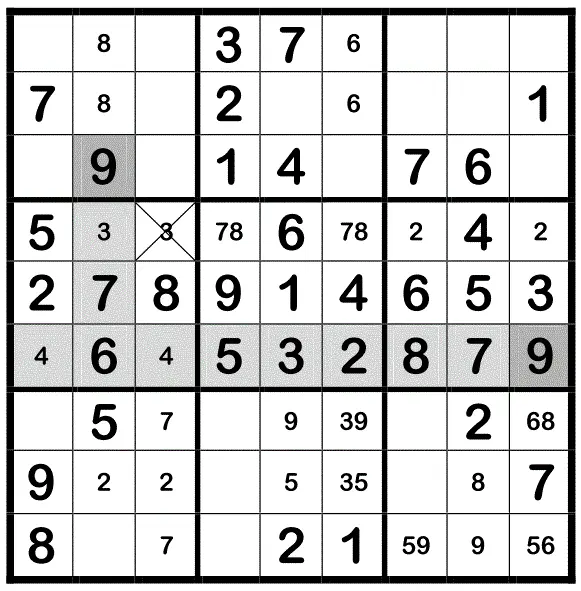
Scan 9:D9 in Q8 und Q9

Die Neunen in Q1+6 ergeben eine echte 9in Q4.

Hier kommt es zu einer weiteren Besonderheitdes Duplex-Verfahrens, denn in diesem Feld steht schon eine Duplex-3. Nachdem die 9hier als Echte eingetragen wurde, wird die übrig gebliebene und nun einzeln stehende Duplex-3 damit ebenfalls zur echten 3.

Wenn sich, wie im vorliegenden Fall, eine neue Zahl (bzw. ein neues Zahlenpärchen) ergibt, verfolgen wir immer sofort deren Auswirkungen auf das gesamte Sudoku.

(In diesem Fall hat die neue 3zwar keine Auswirkungen, d. h. man kann mit ihr momentan keine weiteren echten bzw. Duplex-Dreier erzeugen, aber das ist nicht immer so.)

Damit ist der Scan-Durchgang für die Zahlen von 1 – 9 abgeschlossen.

Nächster Schritt:

Man sucht jetzt nach einer Zeile, einer Spalte oder einem Quadranten, in der/dem nur noch sehr wenige Zahlen fehlen und ergänzt (wenn möglich) die fehlenden Zahlen.

Im vorliegenden Fall bietet sich Q6 an:

Die 1in Q3 erzeugt in Q6 eine echte 1im Feld der linken Duplex-2, damit wird die rechte D2 zur echten 2.Diese beiden neuen Zahlen haben nun die weiter oben beschriebenen Auswirkungen, die wir sofort verfolgen: So erhalten wir ein Einser-Duplexpaar in Q4, eine echte 2in Q3 und eine 2in Q1. Dies hat zur Folge, dass die (rechte) Duplex-Zwei in Q7 gelöscht und damit die andere D2 zur echten 2wird.

(Sie können jetzt die Bleistift-D2 hinter der neugewonnenen 2in Q6+7 ausradieren, weil der Scan für die Zahl 2 abgeschlossen ist.)

Die Einsen in Q3, Q6 und Q8 ergeben eine echte 1in Q9. In diesem Feld steht jedoch eine D8, die jetzt mit einer 1überschrieben wird und die übrig gebliebene D8 zur Echten macht. Diese 8löscht die im gleichen Feld befindliche D6. Damit wird die andere D6 zur Echten und entfernt D5. Die verbleibende D5 wird zur Echten und entfernt die D9, sodass nur noch eine D9 übrig bleibt, die damit ebenfalls zur echten 9wird!